矩阵连乘（C语言）

矩阵连乘（C语言）

参考链接：https://blog.csdn.net/qq_32919451/article/details/80643118

问题描述

给定n个矩阵｛A1,A2,…,An｝，其中Ai与Ai+1是可乘的，i=1，2…，n-1。如何确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少。例如，给定三个连乘矩阵{A1，A2，A3}的维数分别是10 * 100，100 * 5和5 * 50，采用（A1A2）A3，乘法次数为101005+10550=7500次，而采用A1（A2A3），乘法次数为100 * 5 * 50+10 * 100 * 50=75000次乘法，显然，最好的次序是（A1A2)A3，乘法次数为7500次。

分析最优解结构

此问题最难的地方在于找到最优子结构。对乘积A1A2…An的任意加括号方法都会将序列在某个地方分成两部分，也就是最后一次乘法计算的地方，我们将这个位置记为k，也就是说首先计算A1…Ak和Ak+1…An，然后再将这两部分的结果相乘。
最优子结构如下：假设A1A2…An的一个最优加括号把乘积在Ak和Ak+1间分开，则前缀子链A1…Ak的加括号方式必定为A1…Ak的一个最优加括号，后缀子链同理。
一开始并不知道k的确切位置，需要遍历所有位置以保证找到合适的k来分割乘积。

建立递归关系

构建辅助表，解决重叠子问题

从第二步的递归式可以发现解的过程中会有很多重叠子问题，可以用一个nXn维的辅助表m[ n ] [ n ] ，s[n] [n]分别表示最优乘积代价及其分割位置k 。
辅助表s[n] [n]可以由2种方法构造：

1. 一种是自底向上填表构建，该方法要求按照递增的方式逐步填写子问题的解，也就是先计算长度为2的所有矩阵链的解，然后计算长度3的矩阵链，直到长度n；
2. 另一种是自顶向下填表的备忘录法，该方法将表的每个元素初始化为某特殊值(本问题中可以将最优乘积代价设置为一极大值)，以表示待计算，在递归的过程中逐个填入遇到的子问题的解。

对于一组矩阵:A1(30x35),A2(35x15),A3(15x5),A4(5x10),A5(10x20),A6(20x25) 个数N为6

那么p数组保存它们的行数和列数：p={30,35,15,5,10,20,25}共有N+1即7个元素

p[0],p[1]代表第一个矩阵的行数和列数，p[1],p[2]代表第二个矩阵的行数和列数…p[5],p[6]代表第六个矩阵的行数和列数

计算最优值

构造最优解

代码实现

#include <stdio.h>
#include <stdlib.h>
//MAXSIZE为数组数字个数
#define MAXSIZE 6
#include <limits.h>
int n = MAXSIZE-1;//矩阵个数
int a[MAXSIZE] = {2,3,5,8,6,5};//全局设置内容
int t[MAXSIZE][MAXSIZE]; //备忘录


int m[MAXSIZE][MAXSIZE];          //m[i][j]存储子问题的最优解
int s[MAXSIZE][MAXSIZE];           //s[i][j]存储子问题的最佳分割点

//方法一：备忘录法优化
int F(int left,int right)
{
    int i=0,lefttimes,righttimes,wholetimes;
    int min=10000;
    int k;
    if(left==right) return 0;
    if(t[left][right]>0)
    {
        return t[left][right];
    }
    for(i=left;i<right;i++)
    {
        lefttimes = F(left,i);
        righttimes = F(i+1,right);
        wholetimes = lefttimes+ righttimes+a[left]*a[i+1]*a[right+1];
        if(wholetimes < min)
        {
            min = wholetimes;
        }
    }
    t[left][right] = min;
    return min;
}

//方法二：自底向上
void matrix(int n,int m[][n],int s[][n],int p[])
{

    int i,r,k,j;
    for(i=0;i<=n;i++)
    {
        for(j=0;j<=n;j++)
        {
            m[i][j]=-1;
        }
    }
    for(i=1;i<=n;i++)
        m[i][i]=0;                  //最小子问题仅含有一个矩阵 ，对角线全为0
    for(r=2;r<=n;r++)//r表示矩阵的长度(2,3…逐渐变长)
        for(i=1;i<=n-r+1;i++)//行循环
        {
            int j=i+r-1;//从第i个矩阵Ai开始,长度为r,则矩阵段为(Ai~Aj)
            //求(Ai~Aj)中最小的,其实k应该从i开始，但先记录第一个值，k从i+1开始，这样也可以。
            //例如对(A2~A4),则i=2,j=4,下面一行的m[2][4]=m[3][4]+p[1]*p[2]*p[4],即A2(A3A4)
            m[i][j] = m[i+1][j]+a[i-1]*a[i]*a[j];
            s[i][j]=i;//记录断开点的索引
            for(int k=i+1;k<j;k++)//循环求出(Ai~Aj)中的最小数乘次数
            {
                //将矩阵段(Ai~Aj)分成左右2部分(左m[i][k],右m[k+1][j]),
                //再加上左右2部分最后相乘的次数(p[i-1] *p[k]*p[j])
                int t = m[i][k]+m[k+1][j]+a[i-1]*a[k]*a[j];
                if(t<m[i][j])
                {
                    m[i][j] = t;
                    s[i][j] = k;
                    //保存最小的,即最优的结果
                }
            }
        }
    for(i=1;i<MAXSIZE;i++)
    {
        for(j=1;j<MAXSIZE;j++)
        {
            printf("%5d",m[i][j]);
        }
        printf("\n");
    }
    printf("矩阵连乘最小次数：%d\n",m[1][n]);

    for(i=0;i<MAXSIZE;i++)
    {
        for(j=0;j<MAXSIZE;j++)
        {
            printf("%5d",s[i][j]);
        }
        printf("\n");
    }
    printf("矩阵连乘的形式：");
    printmatrix(1,n);
}
//递归打印输出
void printmatrix(int leftindex,int rightindex)
{
    if(leftindex==rightindex)
        printf("A%d",leftindex);
    else{
        printf("(");
        printmatrix(leftindex,leftindex+s[leftindex][rightindex]);
        printmatrix(leftindex+s[leftindex][rightindex]+1,rightindex);
        printf(")");
    }
}

int main()
{
    int i,j,x,p;
    for(i=0;i<MAXSIZE;i++)
    {
        for(j=0;j<MAXSIZE;j++)
        {
            t[i][j]=0;//备忘录清零
        }
    }
    int times = F(0,MAXSIZE-2);
    printf("矩阵连乘最小次数：%d\n",times);
    matrix(n,m,s,a);
    return 0;
}

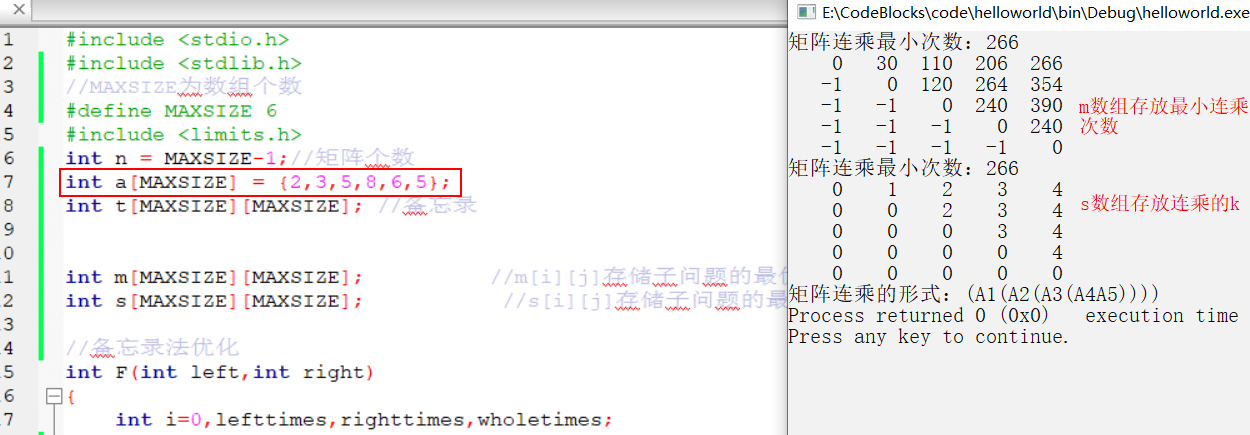
截图