大学物理电磁学——磁场对载流导线的作用

磁场对载流导线的作用

一、安培定律

方法：微元分割+积分求和

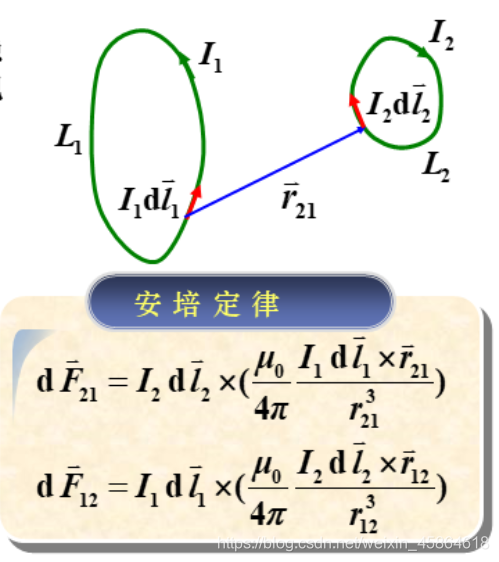第一个式子表示，电流元2对1的作用力。
注意：

• 两个电流元之间的作用力不满足牛顿第三定律。
• 但是两个载流闭合导线之间的相互作用力满足牛顿第三定律。

安培力的一般形式：
$d\vec{F}=Id\vec{l}\times \vec{B}$
实质：
导线中作定向移动的电子在洛伦兹力的作用下，通过导线内部的自由电子和晶格之间的 作用，使导线在宏观上表现出受到磁力的作用。

二、磁场对载流导线的作用

任意形状的载流导线在外磁场中受到的安培力
$\vec{F}={\int }_{L}d\vec{F}={\int }_{L}Id\vec{l}\times \vec{B}$
当电流与磁场强度都恒定时，有结论：

均匀磁场中任意载流共面导线所受的磁场力=载有相同电流的直导线所受的磁场力

三、磁场对载流线圈等等作用

推论：

均匀磁场中任意载流共面闭合线圈所受的磁场力的合力等于0。

但是，力矩并不一定等于0。
$M=BISsin\theta$
其中，$S$是闭合线圈面积，$\theta$是载流线圈的法向与$B$的夹角。
前面我们学习过电流圈的磁矩
$\overrightarrow{P_m}=IS\vec{n}$
那么，$\vec{M}=\overrightarrow{P_m}\times \vec{B}$
注意：

1. 适用于均匀磁场中的任意载流平面线圈。
2. 对于N匝线圈：$\overrightarrow{P_m}=NIS\vec{n}$
3. • 当$\vec{n}$与$\vec{B}$平行时，$M$=0，系统区域稳定平衡。
   • 当$\vec{n}$与$\vec{B}$垂直时，$M$最大，系统受到最大磁力矩。
   • 当$\vec{n}$与$\vec{B}$反向平行时，$M$=0，系统区域处于不稳定平衡。

四、磁力的功

1. 载流导线在均匀磁场中运动时磁力做的功
   $W=Fs=BIls=I\Delta {\Phi }_m$
2. 载流线圈受磁力矩M的作用
   产生角位移，仍有$W=I\Delta {\Phi }_m$

课堂小结