二叉排序树

1.定义

二叉排序树(BST)，又称为二叉树搜索树和二叉查找树。

定义：

• 如果它的左子树非空，则左子树中的所有结点的值都小于根节点的值
• 反之，若右子树非空，则右子树上所有的结点的值都大于等于根节点的值
• 其左右子树本身也是二叉排序树

二叉排序树

该二叉树的中序遍历的结果一定是有序的，如上的中序遍历的结果为3,12,24,37,45,53,61,78,90,99

2.二叉排序树的操作

二叉排序树有关的一些操作可以包含search查找，minimum查找最小值，maximum查找最大值，predecessor，successor查找某个结点的前驱和后继结点，insert插入节点，delete删除某一结点等操作，我们将围绕这些操作开始讲解。

下面你将看到如何在O(h)的时间复杂度完成这些操作，h代表树的高度。

如果二叉排序树是一个完全二叉树，那么树的高度为logn +1，其中n为树的结点数，所以O(h)就为O(logn)，如果不是完全二叉树那么时间复杂度就会升高，最坏情况下树的结构为一条线性链，时间复杂度就为O(n)。为了解决这种高度不平衡的情况，可以使用平衡二叉树

首先我们定义出二叉排序树的数据结构，为了方便，我采用的是三叉链来表示二叉树：

public class BinarySortTree {
    //根结点
    private TreeNode root;

    //二叉搜索树的结点结构，采用三叉链表
    class TreeNode {
        int value;
        TreeNode parent; //父结点
        TreeNode left;
        TreeNode right;

        public TreeNode(int value) {
            this.value = value;
        }
    }

    //先把中序遍历定义好
    public void inOrder() {
        inOrder(root);
    }
    private void inOrder(TreeNode treeNode) {
        if (treeNode == null) return;
        inOrder(treeNode.left);
        System.out.print(treeNode.value + " ");
        inOrder(treeNode.right);
    }
}

2.1插入

首先是二叉树结点的插入insert，如图所示，插入一个结点只需要找到该插入结点的位置，如插入13这个结点，先从树根开始，13是大于15的，这时候13应该插入到根结点的右子树，又因为根结点的右子树不为空，所以继续向下移动，找到18，把18作为根节点继续比较……直到找到一个根节点，该根节点的左子树或右子树是空的，且空着的位置正好是要插入的结点的位置，就停止。

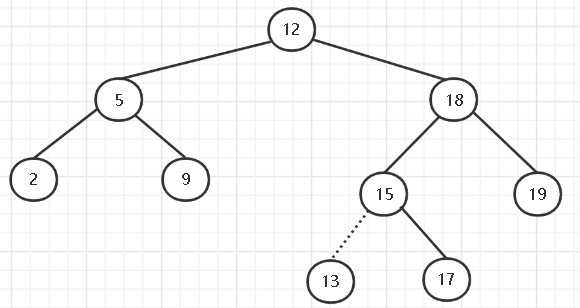
 代码如下：

public void insert(int val) {
    //需要插入的结点
    TreeNode insert = new TreeNode(val);
    //pre记录某一个子树的根
    TreeNode pre = null, now = root;
    //now为空时就代表该空着的位置就是插入结点的位置
    while (now != null) {
        pre = now;
        if (insert.value < now.value)
            now = now.left;
        else now = now.right;
    }
    insert.parent = pre;
    if (pre == null) 
        root = insert;
    else if (insert.value < pre.value)
        pre.left = insert;
    else pre.right = insert;
}

我这里采用的是迭代，也可以使用递归更方便。该过程是一个向下移动查找插入位置的过程，时间复杂度为O(h)。

2.2查找

过程如下：

• 若等于根节点则成功返回
• 如果小于根节点，则查其左子树
• 否则的话查其右子树

该过程从树根开始查找，沿着一条树的简单路径进行查找，如果未找到就返回空

代码如下：

public TreeNode search(int val) {
    TreeNode p = root;
    while (p != null) {
        //找到了
        if (val == p.value)
            return p;
        else if (val < p.value) //在根的左子树
            p = p.left;
        else p = p.right;  //在根的右子树
    }
    return null;
}

时间复杂度为O(h)，也开始以使用递归来实现，自己可以实现一下

3.3最大元素和最小元素

该操作也比较简单， 我们从图中就可知：最小的元素往往是最左边的一个结点，最大的元素是最右边的那个结点，所以只需要一直跟这向下寻找即可。

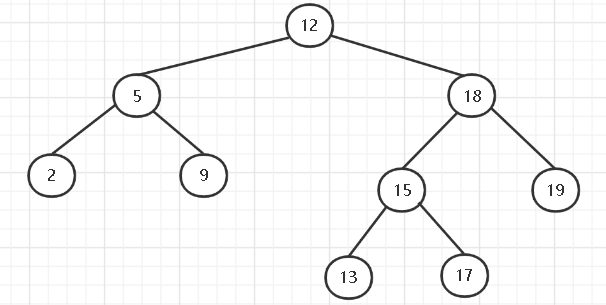
代码：

public TreeNode maximum(){
    TreeNode p = root;
    while(p.right!=null)
        p = p.right;
    return p;
}

public TreeNode minimum(){
    TreeNode p = root;
    while(p.left!=null)
        p = p.left;
    return p;
}

时间复杂度也是O(h)，根据这一特性搭配二叉搜索树的删除操作，可以应用于优先队列。

3.4前驱和后继

首先是求某个结点的前驱，分两种情况：

• 该结点的左子树不为空，那么前驱就是左子树中值最大的那个结点，求最大结点只需改变一下前面的maximum即可
• 左子树如果为空，那么前驱结点就必须往上面找，因为右子树都是大于它的不可能在右子树上，此时只需在上面找到一个最小的值，这个过程也分几种情况：
  • 如果当前结点是父结点的左孩子，那么父节点是大于当前结点的，此时还要继续往上走
  • 反之如果是父结点的右孩子，那么父节点就是小于孩子结点的，也就是它的前驱了
  • 直到找到最上层的父节点，还是都大于当前结点，则该结点没有前驱

求结点的后继也是类似的思想

//求结点的前驱
public TreeNode predecessor(TreeNode node) {
    if (node.left != null) return maximum(node.left);
    TreeNode pre = node.parent;
    while (pre != null && pre.left == node) {
        node = pre;
        pre = node.parent;
    }
    return pre;
}
public TreeNode maximum(TreeNode node) {
    TreeNode p = node;
    while (p.right != null)
        p = p.right;
    return p;
}

//求结点的后继
public TreeNode successor(TreeNode node) {
    if (node.right != null) return minimum(node.right);
    TreeNode pre = node.parent;
    while (pre != null && pre.right == node) {
        node = pre;
        pre = node.parent;
    }
    return pre;
}
public TreeNode minimum(TreeNode node) {
    TreeNode p = node;
    while (p.left != null) p = p.left;
    return p;
}

同样的，时间复杂度依旧为O(h)。

从上面的操作来看，可以看到一个性质：如果一个结点有左孩子，那么该结点的前驱是没有右孩子的；如果该结点有右孩子，那么该结点的后继是没有左孩子的。

证明：假设节点x有两个子结点。然后它的后继元素是右子树的最小元素，如果它有左孩子，那么它就不是最小的元素。所以，它不能有左孩子。类似地，前驱必须是左子树的最大元素，因此不能有右子元素。

3.5删除

删除结点的操作相对比较复杂。

• 将因删除结点而断开的二叉链表重新链接起来
• 反之重新链接后树的高度增加

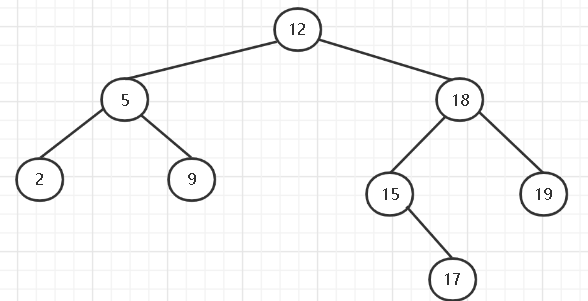
 分为三种情况(参考上图)：

• 删除一个没有孩子的结点，只需要简单的删除即可
• 删除只有一个孩子的结点，只需把它的唯一的孩子提升放在它的位置即可
• 删除有两个孩子的结点复杂一点：先找到该结点的后继结点，用它的后继结点来接替该结点，根据前面的性质，如果一个结点有两个孩子，那么它的后继结点没有左孩子。所以将后继结点换上去时，只需考虑它的右子树怎么存放。分两种情况：
  • 如果要删除结点的后继结点就是它的右孩子，那么就直接将后继结点提升上去，如下图，要删除z这个结点，它的后继结点就是y，此时用y替代z，别的不需要变

• • 如果后继结点不是它的右孩子，也是先把后继结点替换过去，然后后继结点的右子树变为原来后继结点的父结点的左孩子。如下图，删除z结点，把y替换上去，但是y可能会有右孩子，把右孩子x变为r的左孩子。 

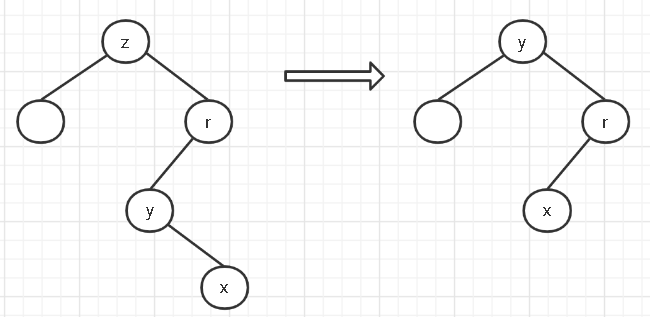
        代码：

//删除结点
public void delete(TreeNode node) {
    //1.左子树为空的情况，右子树可能为空或不为空
    if (node.left == null) {
        transplant(node, node.right);
    }
    //2.右子树为空，左子树不为空的情况
    else if (node.right == null) {
        transplant(node, node.left);
    }
    //3.左右子树都存在的情况
    else {
        TreeNode successor = minimum(node.right);//找后继
        //3.1后继不是要删除结点的右孩子，
        if (successor.parent != node) {
            //后继结点的孩子提升到后继结点的位置
            transplant(successor, successor.right);
            //修改后继结点的右孩子指针，为提升为要删除结点的位置做准备
            successor.right = node.right;
            successor.right.parent = successor;
        }
        //3.2后继结点是右孩子时，直接提升上去
        transplant(node, successor);
        successor.left = node.left;
        successor.left.parent = successor;
    }
}

//用一棵子树替换另一棵子树，并成为其双亲的孩子结点，q替换p，该方法没有更新q的左孩子和右孩子
public void transplant(TreeNode p, TreeNode q) {
    //p为二叉搜索树的父节点
    if (p.parent == null) {
        root = q;
    } else if (p.parent.left == p) {
        p.parent.left = q;
    } else {
        p.parent.right = q;
    }
    if (q != null) {
        q.parent = p.parent;
    }
}

时间复杂度依然为O(h)，因为只有查找后继比较费时，其余的修改操作都是常数级的。

如果以上的二叉排序树本来就是排序好的一条链，那么时间复杂度变为O(n)，我们必须确保二叉搜索树的随机性，期望高度为O(logn)