关于数据类型的取值范围

Y.YL

已于 2023-10-13 16:51:09 修改

阅读量1k

点赞数

文章标签： c++

于 2023-10-08 14:50:10 首次发布

。

本文链接：https://blog.csdn.net/weixin_45916959/article/details/133681608

版权

直观图

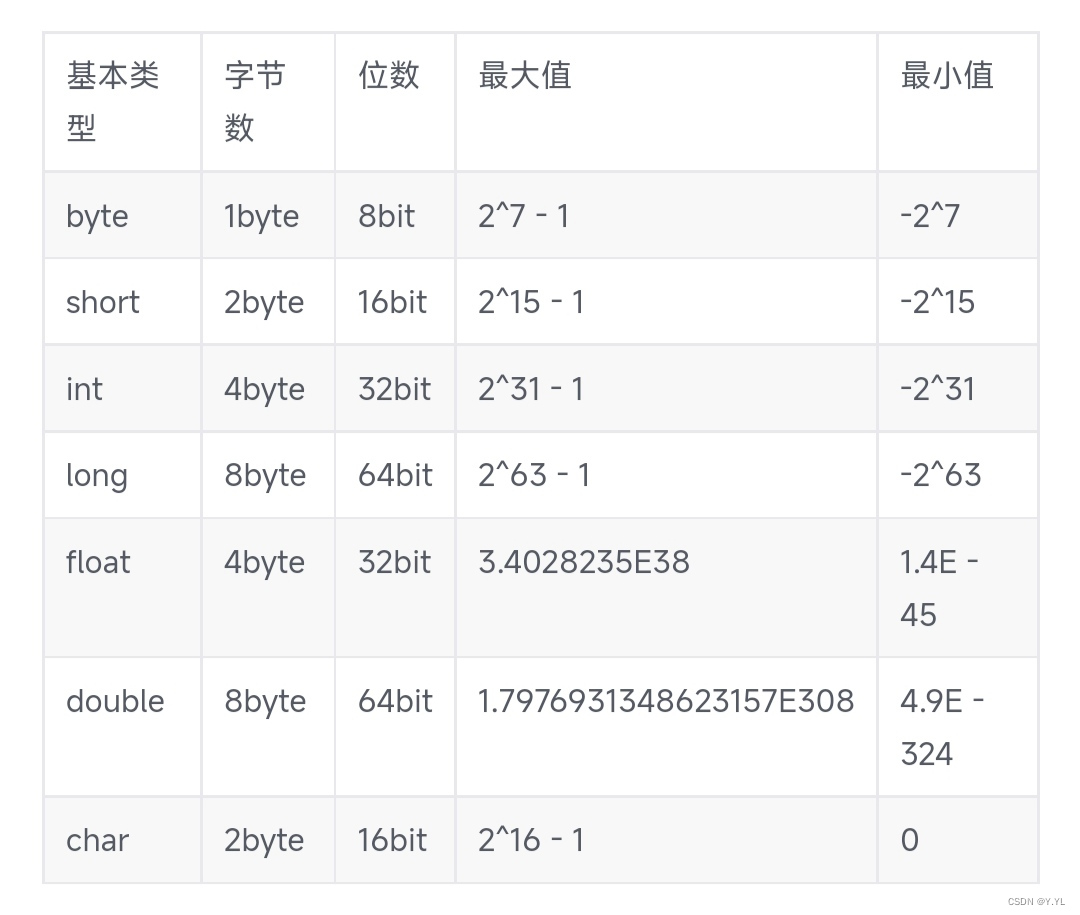
在这里插入图片描述

double

double类型的数据最小值是4.940656458412465442e-324，是由于double类型采用的是IEEE 754标准的浮点数表示方法。在这种表示方法中，double类型的数据使用64位来存储，其中1位用于符号位（表示正负），11位用于指数位，52位用于尾数位。

最小值4.940656458412465442e-324对应的指数位全为0，尾数位全为1，符号位为0，代表一个非常接近于0的正数。根据IEEE 754标准，指数位全为0代表的指数是-1022（实际上是-1023加上一个隐含的1），所以最小值可以表示为2^(-1022)。

这个值非常接近于0，但不等于0。在计算机内部，0无法精确地用浮点数表示，因为尾数位全为0时代表的是无穷大或NaN（非数字）。所以，最小值4.940656458412465442e-324是double类型能够表示的最接近于0的正数。

问：什么是IEEE 754标准？

IEEE 754标准是一种定义了浮点数表示和运算的规范，它被广泛应用于计算机硬件和软件中。该标准定义了两种浮点数格式：单精度和双精度。—在IEEE 754标准中，双精度浮点数（double）被表示为64位二进制数。其中，第1位表示符号位（0代表正数，1代表负数），接下来的11位表示指数部分，剩下的52位表示尾数部分。

具体表示方法如下：1. 符号位：最左边的1位用于表示正负号，0表示正数，1表示负数。2. 指数部分：接下来的11位用于表示指数。实际的指数值是这个无符号整数减去一个偏移值（这里是1023），所以指数的范围是-1022到+1023。这允许浮点数表示非常大和非常小的数字。3. 尾数部分：剩下的52位用于表示尾数。尾数采用了一种称为“隐藏位”的技术，即省略了二进制小数的整数部分的1，只存储小数部分的二进制位。这使得可以用更多的位数来表示小数部分，提高了浮点数的精度。

根据上述表示方法，双精度浮点数可以表示非常大和非常小的数字，并且能够提供较高的精度。然而，由于浮点数在计算机中的表示是近似值，一些运算可能会导致舍入误差。

问：为什么double类型的指数部分指数的范围是-1022到1023？为什么不是-1023～1023？

double类型是一种浮点数类型，在计算机中表示浮点数使用了IEEE 754标准。在该标准中，double类型使用64位来表示一个浮点数，其中11位用来表示指数部分。

对于指数部分，最左边的一位是符号位，表示正负，接下来的11位用于表示指数大小。符号位取1表示负数，取0表示正数。指数部分由偏移编码表示，即真实的指数值加上一个偏移量。

对于double类型来说，偏移量是1023，所以指数范围可以表示为-1022到1023。如果指数部分在真实值上再加上1023（偏移量），最终表示的指数范围就是-1023到1023。

为什么不是-1023～1023呢？这是因为在IEEE 754标准中，为了保留一份特殊的编码，用于表示特殊情况，例如无穷大（Infinity）和非数值（NaN），所以将最小的指数范围-1023保留作为特殊情况下的指数编码。

总之，double类型的指数部分指数范围为-1022到1023，其中-1023被保留作为特殊情况下的编码，用于表示无穷大和非数值。
在这里插入图片描述