欧氏距离和标准化欧氏距离

1. 欧氏距离：类似于数学中求两个点之间的距离。

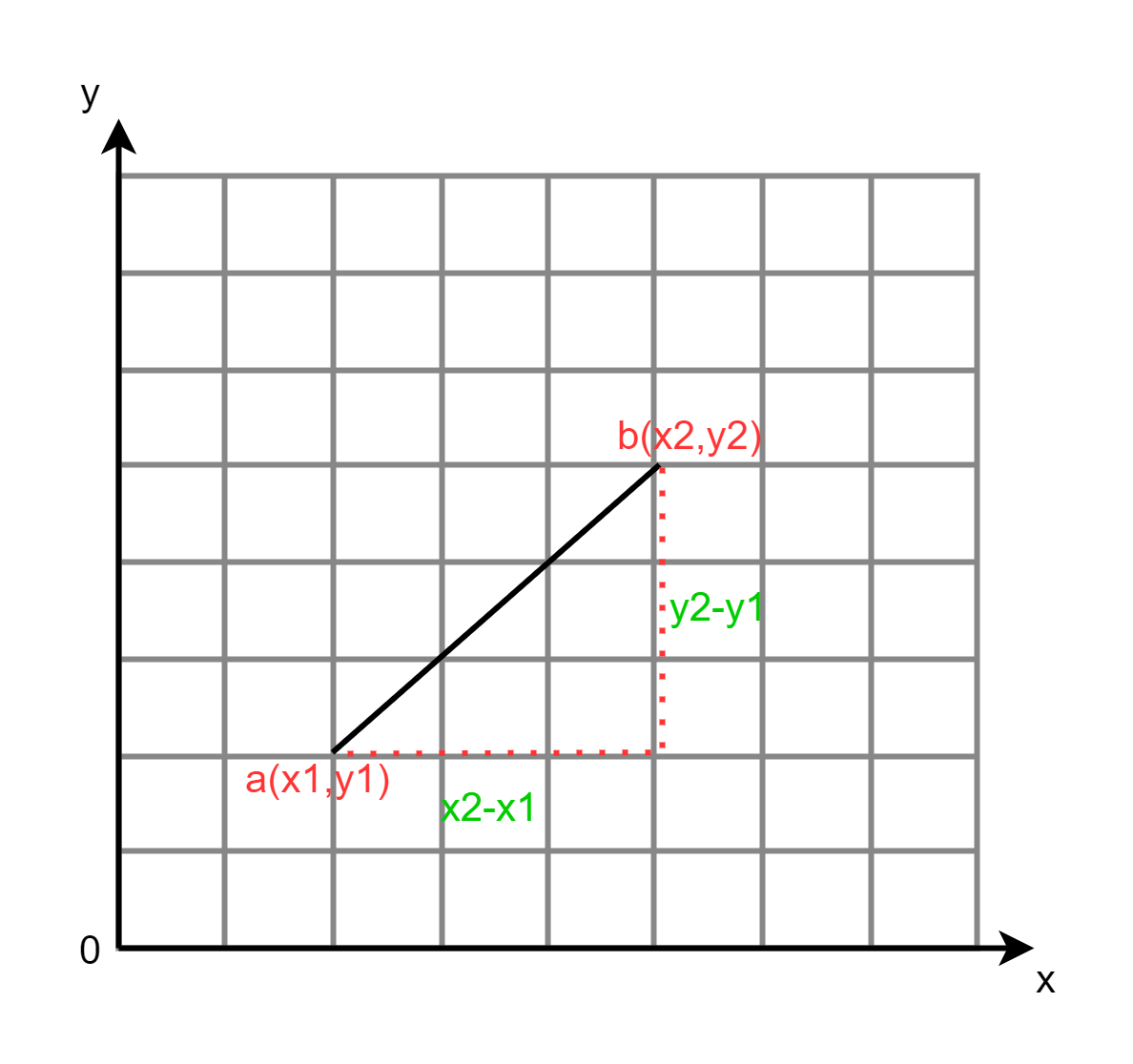
•  二维平面上点a(,)与b(,)间的欧式距离：

• 三维平面上点a(,,)与b(,,)间的欧式距离：

• n维平面上点a(,,...,)与b(,,...,)间的欧式距离(两个n维向量)：

2.标准化欧氏距离

  标准化欧氏距离是对欧氏距离缺点的一种改进。
  思路：既然数据各维分量的分布不一样，那先将各个分量都“标准化”到均值、方差相等。假设样本集X的均值为m，标准差为s，X的“标准化变量”表示为：
“标准化变量”表示为：

标准化欧氏距离公式：

  如果将方差的倒数看成一个权重，也可称之为加权欧氏距离。