数据结构课设——稀疏矩阵的操作

随机森林不是森林

已于 2023-10-01 17:38:04 修改

阅读量343

点赞数

分类专栏：本科课程设计与各类作业汇总文章标签：数据结构矩阵

于 2023-10-01 16:54:28 首次发布

本文链接：https://blog.csdn.net/weixin_46008839/article/details/133466523

版权

本科课程设计与各类作业汇总专栏收录该内容

20 篇文章 4 订阅

订阅专栏

第一章设计目的

1．掌握多维数组的逻辑结构和存储结构。

2．掌握稀疏矩阵的压缩存储及基本操作。

3. C++语言简介：C++是C语言的继承，它既可以进行C语言的过程化程序设计，又可以进行以抽象数据类型为特点的基于对象的程序设计，还可以进行以继承和多态为特点的面向对象的程序设计。C++擅长面向对象程序设计的同时，还可以进行基于过程的程序设计，因而C++就适应的问题规模而论，大小由之。C++不仅拥有计算机高效运行的实用性特征，同时还致力于提高大规模程序的编程质量与程序设计语言的问题描述能力。

第二章需求分析

1．稀疏矩阵采用十字链表表示，求两个具有相同行列数的稀疏矩阵A和B的相加矩阵C，并输出矩阵C。

2．求出A的转置矩阵D，输出D）。

3．求两个稀疏矩阵A和B的相乘矩阵E，并输出E。

第三章总体设计

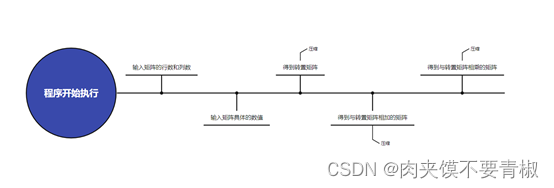
第四章详细设计与实现

1、为要进行计算的矩阵创建结构体：

typedef struct CompressionMatrix {

       int data;

       int row;

       int column;

} CompressionMatrix;

2、矩阵相乘：

void multiply(int User_data[][MAXSIZE],int conversionmatrix[][MAXSIZE],int row,int column)

{
            for(int j = 0;j<row;j++)//因为是和转置后的相乘，所以乘后的矩阵的长和宽都等于原来矩阵的row

            int multiplydatasum;

            for(int k = 0;k<column;k++)

            {

                Multiplydatasum= = User_data[i][k]*conversionmatrix[k][j]+multiplydatasum;                                                                             

            multiply_data[i][j] = multiplydatasum;

            multiplydatasum = 0;

        }

3.矩阵相加

（1）.判断是否有相加的条件（长宽相等）。

if(row!=column)

    {

        cout<<"长和宽不相同，不能相加！"; //矩阵相加的限制

    }

（2）.当两个矩阵长和宽相等时，即可以相加，执行else内的语句，通过两个双重循环获取两个矩阵并相加：

else{

    int add_data[MAXSIZE][MAXSIZE];

    for(int i = 0;i<row;i++)

    {

        for(int j = 0;j<column;j++)

        {

            add_data[i][j] =  User_data[i][j]+conversionmatrix[i][j];

        }

    }

    for(int i = 0;i<row;i++)

     {

        cout<<endl;

        for(int j = 0;j<column;j++)

        {

            cout<<add_data[i][j]<<' ';

        }

     }

     putchar('\n');

     putchar('\n');

     cout<<"压缩后："<<endl;

     compress(row,column,add_data);

   }

4.矩阵转置：

用双重循环将原矩阵的行和列交换即可得到原矩阵的转置矩阵：

for(int i = 0;i<row;i++)

     {

        for(int j = 0;j<column;j++)

        {

            conversionmatrix[j][i] =  User_data[i][j];//交换行列顺序即转化

        }

     }

5.对矩阵进行压缩：

将矩阵的数据压入压缩矩阵中：

CompressionMatrix matrix_1[MAXSIZE];//创建压缩矩阵  这里使用的是压缩矩阵里的稀疏矩阵的压缩，使用三元数组对矩阵进行存储

    for(int i = 0;i<row;i++)

    {for(int j = 0;j<column;j++)

        {

            if(User_data[i][j]!=0)

            {

                matrix_1[count].row = i+1;

                matrix_1[count].column = j+1;

                matrix_1[count].data = User_data[i][j];

                count++;

            }

        }

    }

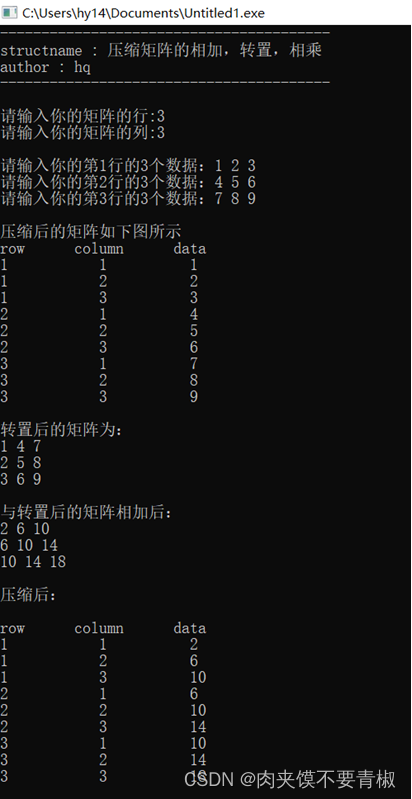
    print(matrix_1,count);}

第五章测试

测试用例：

输入

具体值

相加

相乘

转置矩阵

3行3列

1 2 3

4 5 6

7 8 9

2 6 10

6 10 14

10 14 18

14 32 50

32 77 122

50 122 194

1 4 7

2 5 8

3 6 9

2行3列

44 96 33

71 52 30

不可相加！

12241 9106

9106 8645

44 71

96 52

33 30

4行5列

5 9 6 5 0

9 6 3 2 0

7 4 1 5 8

1 5 1 4 2

不可相加！

167 127 102 116

127 130 100 122

102 100 155 120

116 2 120 127

4 9 7 9

9 6 4 5

6 3 1 1

5 2 5 4

0 0 8 2

4行4列

7 8 9 9

5 6 2 4

7 1 0 3

5 2 2 1

14 13 16 14

13 12 3 6

16 3 0 5

14 6 5 2

275 137 84 78

137 81 53 45

84 53 59 40

78 45 40 34

7 5 7 5

8 6 1 2

9 2 0 2

9 4 3 1

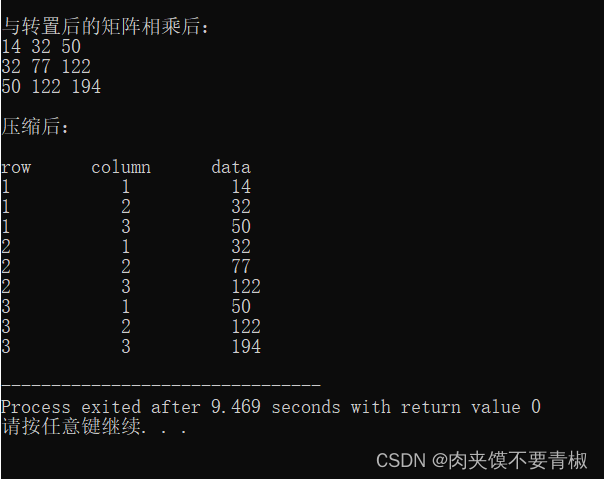
第六章时间复杂度分析

1.矩阵相乘

相乘方法中最高用了3个嵌套循环，时间复杂度为O（n*n*n）.

2.矩阵转置

两个双重循环计算次数为n*n+n*n,时间复杂度为O(n*n);

3.矩阵相加

和矩阵转置一样，两个双重循环计算次数为n*n+n*n,时间复杂度为O(n*n);

4.矩阵压缩

两个循环嵌套，时间复杂度为O(n*n)。

第七章源码

#include<iostream>
#define MAXSIZE 100
using namespace std;

typedef struct CompressionMatrix{
    int data;
    int row;
    int column;
}CompressionMatrix;

void print(CompressionMatrix matrix[],int count);
void compress(int row,int column,int User_data[][MAXSIZE]);//注意二维数组传参时需要传入第二维的最大值 
void conversion(int User_data[][MAXSIZE],int row,int column,int conversionmatrix[][MAXSIZE]);
void add(int User_data[][MAXSIZE],int conversionmatrix[][MAXSIZE],int row,int column);
void multiply(int User_data[][MAXSIZE],int conversionmatrix[][MAXSIZE],int row,int column);

int main()
{
    cout<<"----------------------------------------"<<endl;
    cout<<"structname : 压缩矩阵的相加，转置，相乘 "<<endl; 
    cout<<"---------------------------------------- "<<endl;
    cout<<endl;
    int row;
    int column;
    cout<<"请输入你的矩阵的行:";
    cin>>row;
    cout<<"请输入你的矩阵的列:";
    cin>>column;
    int User_data[MAXSIZE][MAXSIZE];//创建稀疏矩阵 
    cout<<endl;
    for(int i = 0;i<row;i++)
    {
        cout<<"请输入你的第"<<i+1<<"行的"<<column<<"个数据："; 
        for(int j = 0;j<column;j++)
        {
            cin>>User_data[i][j];
        }
    }//输入数据完毕
    putchar('\n');
    cout<<"压缩后的矩阵如下图所示";
    compress(row,column,User_data);
    putchar('\n');
    cout<<"转置后的矩阵为：";
    int conversionmatrix[MAXSIZE][MAXSIZE];
    conversion(User_data,row,column,conversionmatrix);   
    putchar('\n'); 
    cout<<"与转置后的矩阵相加后：";
    add(User_data,conversionmatrix,row,column);
    putchar('\n');
    cout<<"与转置后的矩阵相乘后：";
    multiply(User_data,conversionmatrix,row,column);
    return 0;
}

void print(CompressionMatrix matrix[],int count)
{
    cout<<endl;
    cout<<"row"<<"      "<<"column"<<"      "<<"data"<<endl;
    for(int i = 0;i<count;i++)
    {
        cout<<matrix[i].row<<"           "<<matrix[i].column<<"          "<<matrix[i].data<<endl;
    }
} 

void multiply(int User_data[][MAXSIZE],int conversionmatrix[][MAXSIZE],int row,int column)
{
    //因为是转置的，所以肯定满足相乘的条件，因此不用再判断
     int  multiply_data[MAXSIZE][MAXSIZE];
     for(int i = 0;i<row;i++)
     {
        
        for(int j = 0;j<row;j++)//因为是和转置后的相乘，所以乘后的矩阵的长和宽都等于原来矩阵的row 
        {
            int multiplydatasum;
            for(int k = 0;k<column;k++)
            {
                multiplydatasum = User_data[i][k]*conversionmatrix[k][j]+multiplydatasum;//矩阵相乘的定义是第[i,j]元素
                                                                                        //等于A矩阵的第i行的数乘以B矩阵第j列的对应的数的乘积之和 
            }
            multiply_data[i][j] = multiplydatasum;
            multiplydatasum = 0;
        }
     }
        for(int i = 0;i<row;i++)
     {
        cout<<endl;
        for(int j = 0;j<row;j++)
        {
            cout<<multiply_data[i][j]<<' ';
        }
     }
     putchar('\n');
     putchar('\n');
     cout<<"压缩后："<<endl;
     compress(row,row,multiply_data); 
}

void add(int User_data[][MAXSIZE],int conversionmatrix[][MAXSIZE],int row,int column)
{
    if(row!=column)
    {
        cout<<"长和宽不相同，不能相加！"; //矩阵相加的限制 
    }
    else{
    int add_data[MAXSIZE][MAXSIZE];
    for(int i = 0;i<row;i++)
    {
        for(int j = 0;j<column;j++)
        {
            add_data[i][j] =  User_data[i][j]+conversionmatrix[i][j];
        }
    }
    for(int i = 0;i<row;i++)
     {
        cout<<endl;
        for(int j = 0;j<column;j++)
        {
            cout<<add_data[i][j]<<' ';
        }
     }
     putchar('\n');
     putchar('\n');
     cout<<"压缩后："<<endl;
     compress(row,column,add_data); 
   }
}

void conversion(int User_data[][MAXSIZE],int row,int column,int conversionmatrix[][MAXSIZE])
{
     for(int i = 0;i<row;i++)
     {
        for(int j = 0;j<column;j++)
        {
            conversionmatrix[j][i] =  User_data[i][j];//交换行列顺序即转化 
        }
     } 
     for(int i = 0;i<column;i++)
     {
        cout<<endl;
        for(int j = 0;j<row;j++)
        {
            cout<<conversionmatrix[i][j]<<' ';
        }
     }
     putchar('\n');
}

void compress(int row,int column,int User_data[][MAXSIZE])
{
    int count = 0;
    CompressionMatrix matrix_1[MAXSIZE];//创建压缩矩阵  这里使用的是压缩矩阵里的稀疏矩阵的压缩，使用三元数组对矩阵进行存储 
    for(int i = 0;i<row;i++)
    {
        for(int j = 0;j<column;j++)
        {
            if(User_data[i][j]!=0)
            {
                matrix_1[count].row = i+1;
                matrix_1[count].column = j+1;
                matrix_1[count].data = User_data[i][j];//将矩阵中的数据压入压缩矩阵中储存 
                count++;
            }
        }
    } 
    print(matrix_1,count);
}