1.简单的二元函数
举例:,
等等较易实现,用一个函数,并直接返回表达式即可。
def func(x, y):
return x*y*(x+y)/2再分别定义x,y的范围与步长,并设置角度、颜色坐标即可。以函数
为例,以下是实现代码,可供参考:
import math
from matplotlib import pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import mpl_toolkits.mplot3d
from matplotlib import pyplot as plt
from matplotlib import cm
figure = plt.figure()
ax = Axes3D(figure)
X = np.arange(0.0,1.0,0.01)
Y = np.arange(0.0,1.0,0.01)
X,Y = np.meshgrid(X,Y)
# 定义二元函数
def func(x, y):
return x*y*(x+y)/2
Z = func(X,Y)#gist_rainbow
ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap='gist_rainbow')
# 更改可视化角度
ax.view_init(elev=20, azim=150) # elev是仰角,azim是方位角
# 添加颜色条
#fig.colorbar(ax)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()
看一下图像显示效果:
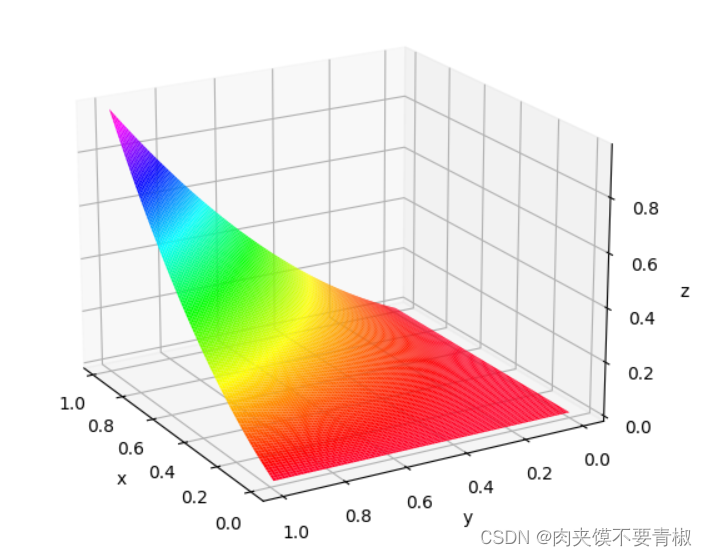
2.复杂的、需要分段的且由变量相进行比较的二元函数
对于此类函数,思想是定义xy的取值范围,在区间内取出足够多个点,然后一个个带入公式比较,再用新的元组将函数值与xy取值绑定,再输出函数三维图像。可以看一下下面这个例子:

实现的代码如下:
import math
from matplotlib import pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import mpl_toolkits.mplot3d
from matplotlib import pyplot as plt
from matplotlib import cm
figure = plt.figure()
ax = Axes3D(figure)
x = np.linspace(0, 1, 50)
y = np.linspace(0, 1, 50)
# 定义二元函数
def func(x, y):
if y<=0.3*x:
return 2*y/3
elif y>=0.3*x and y<=0.6*x:
return -0.4*x+2*y
elif y>=0.6*x and y<=5*x/3:
return (x+y)/2
elif y>5*x/3 and y<=10*x/3:
return -0.4*y+2*x
elif y>10*x/3:
return 2*x/3
else:
return np.nan
# 生成x和y的网格点
X,Y = np.meshgrid(x,y)#创建网格
Z = np.array([[func(x, y) for x, y in zip(row_x, row_y)] for row_x, row_y in zip(X, Y)])
#Z = func(X,Y)#gist_rainbow
ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap='rainbow')
# 更改可视化角度
ax.view_init(elev=20, azim=210) # elev是仰角,azim是方位角
# 添加颜色条
#fig.colorbar(ax)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()
显示效果:

和论文里实现的效果一样:

























 685
685

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








