Datawhale 决策树与集成学习 Task01 决策树

练习题：

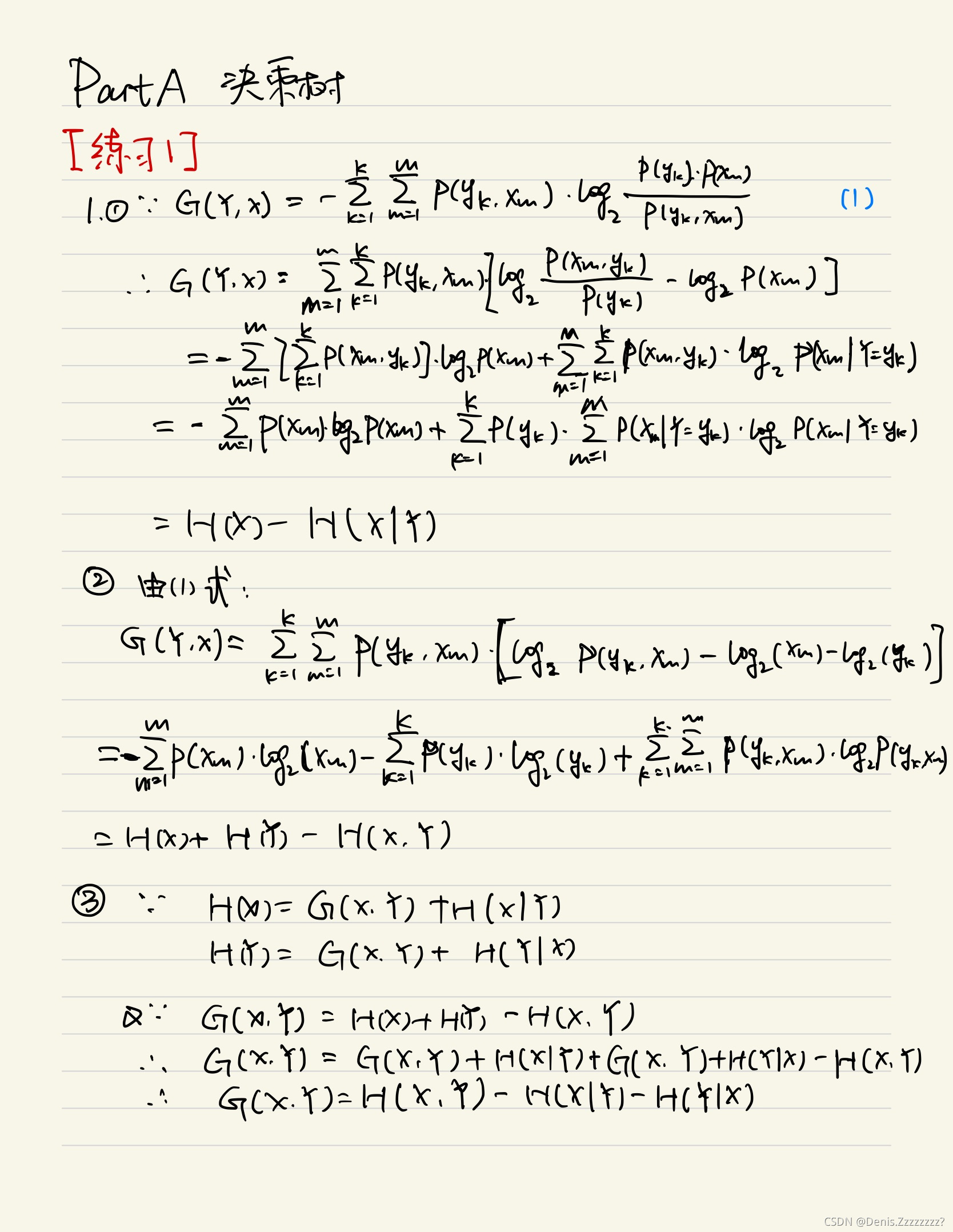
知识回顾

1. ID3、C4.5与CART算法之间有什么异同

算法	异同
ID3	其核心是在决策树的各级节点上，使用信息增益方法的选择标准，来帮助确定生产每个节点时所对应采用的合适属性， 不能自动分箱， 不能剪枝。
C4.5	相对于ID3改进是使用信息增益率来选择节点属性。 克服ID3点不足： ID3只适用于离散的描述属性； C4.5可以处理连续和离散属性； 可以剪枝。
CART	通过构建树、修剪树、评估树来构建一个二叉树。 通过控制树的结构来控制模型： 当终节点是连续变量是——回归树； 当终节点是分类变量是——分类树。

2. 什么是信息增益？它衡量了什么指标？它有什么缺陷？

信息增益是由于特征X的信息而使得类Y的信息的不确定性的减少程度。

衡量了节点分裂之后带来了多少不确定性的降低或纯度的提高。

信息增益的缺陷：可取值数目较多的特征有所偏好。
例如学号作为特征，由于学号独特唯一，条件熵为0，所以纯度会非常高，但是没有节点分裂的意义。

3. sklearn决策树中的random_state参数控制了哪些步骤的随机性？

特征抽取和random_split

4. 决策树如何处理连续变量和缺失变量

C4.5中增加了处理连续变量的方法，用两种方法来将数值特征通过分割转化为类别，它们分别是最佳分割法和随机分割法

5. 基尼系数是什么？为什么要在CART中引入它

由于在计算熵时对数函数log的计算代价较大，CART将熵中的log在p=1处利用一阶泰勒展开，将基尼系数定义为熵的线性近似

6. 什么事树的预剪枝和后剪枝？具体分别是如何操作的？

预剪枝是指树在判断节点是否分裂的时候就预先通过一些规则来阻止其分裂，后剪枝是指在树的节点已经全部生长完成后，通过一些规则来摘除一些子树。

预剪枝：在sklearn的CART实现中，一共有6个控制预剪枝策略的参数，它们分别是最大树深度max_depth、节点分裂的最小样本数min_samples_split、叶节点最小样本数min_samples_leaf、节点样本权重和与所有样本权重和之比的最小比例min_weight_fraction_leaf、最大叶节点总数max_leaf_nodes以及之前提到的分裂阈值min_impurity_decrease。