hdu 2045 不容易系列之(3)—— LELE的RPG难题
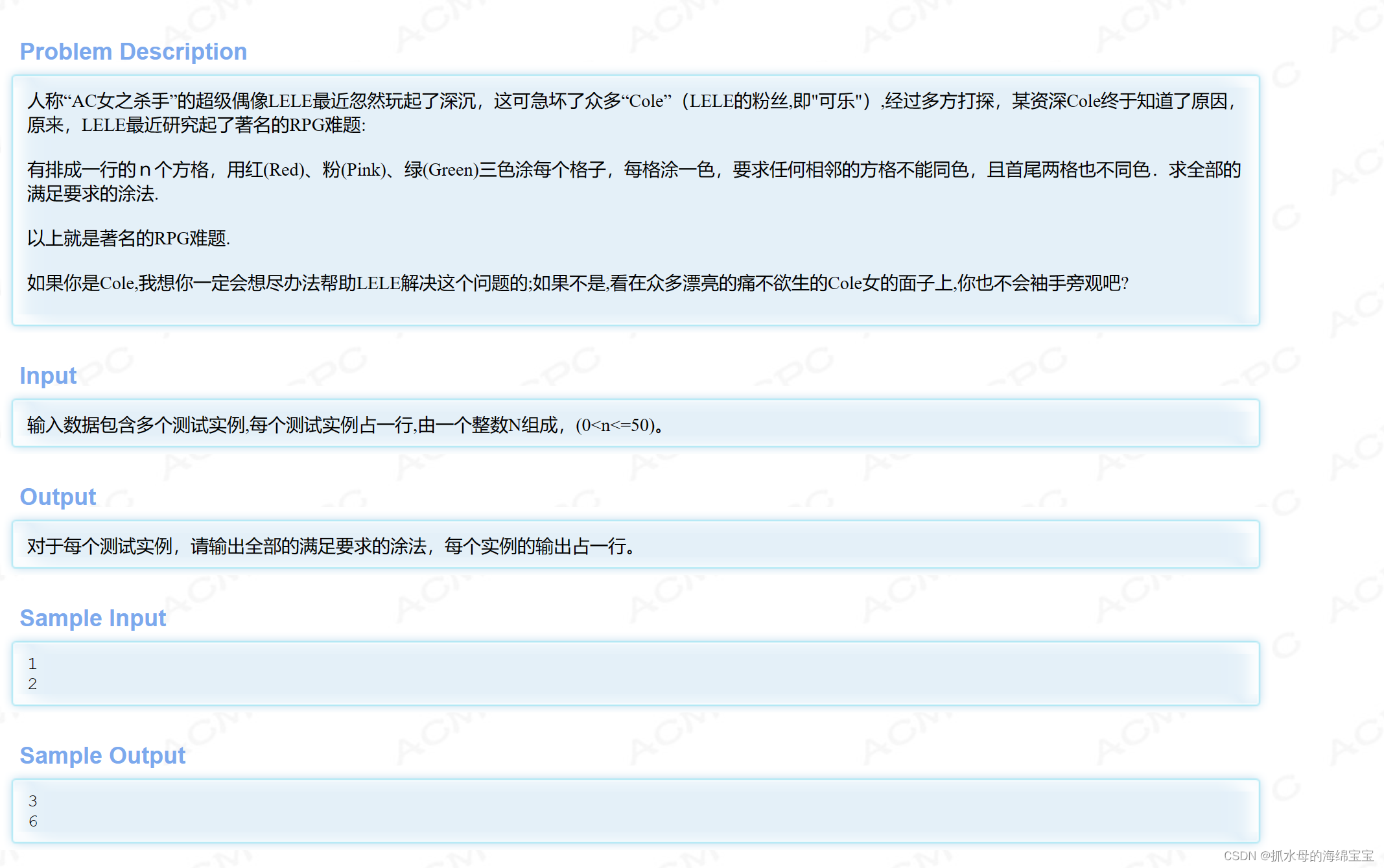
dp 做法,三维数组dp[i][j][k]表示长度为i时,开头颜色为j,结尾颜色为k,不断向后枚举打表,即可得出答案。(递推做法一开始没想出来)
#include<bits/stdc++.h>
using namespace std;
const int maxn = 5e6 + 5;
const double pi = 3.1415927;
const int mod = 1000;
typedef long long ll;
// dp[i][j][k],表示到第i个位置,开头是颜色j,结尾是颜色k的涂法
ll dp[55][4][4];
void init() {
// 长度为1时,每种颜色1种情况
dp[1][1][1] = 1, dp[1][2][2] = 1, dp[1][3][3] = 1;
// 长度为2初始化
for(int i=1;i<=3;i++){
for(int j=1;j<=3;j++){
if (i==j) continue;
dp[2][i][j] = 1;
}
}
for (int i = 3; i <= 50; i++) {
// 枚举开头的颜色,其实可以不用循环
for (int j = 1; j <= 3; j++) {
// 开头为颜色1
if (j == 1){
// 继承长度为i-1的合法种数
dp[i][j][1] = dp[i-1][j][2]+dp[i-1][j][3];
// 长度为i-1时,有1...1和1...3两种情况
dp[i][j][2] = dp[i-1][j][3]+dp[i-1][j][1];
// 长度为i-1时,有1...1和1....2两种情况
dp[i][j][3] = dp[i-1][j][2]+dp[i-1][j][1];
}
if (j==2){
dp[i][j][2] = dp[i-1][j][1]+dp[i-1][j][3];
dp[i][j][1] = dp[i-1][j][3]+dp[i-1][j][2];
dp[i][j][3] = dp[i-1][j][1]+dp[i-1][j][2];
}
if (j==3){
dp[i][j][3] = dp[i-1][j][1]+dp[i-1][j][2];
dp[i][j][1] = dp[i-1][j][2]+dp[i-1][j][3];
dp[i][j][2] = dp[i-1][j][1]+dp[i-1][j][3];
}
}
}
}
void solve() {
int n;
while (cin>>n){
ll ans = 0;
if (n==1){
cout<<3<<'\n';
continue;
}
for(int i=1;i<=3;i++){
for(int j=1;j<=3;j++){
if (i == j) continue;
ans += dp[n][i][j];
}
}
cout<<ans<<'\n';
}
}
int main() {
int T = 1;
// cin >> T;
init();
while (T--) {
solve();
}
return 0;
}```





















 195
195

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








