本章节的研究对象是集中载荷与均匀分布荷载模型,在C语言程序中输入数据,借助Microsoft Excel电子表格对数据进行可视化处理,作出模型的剪力图与弯矩图,让用户更直观地看到模型受力情况。
弯曲应力可视化程序算法流程图如下:
![]()
Part 1.剪力图与弯矩图的可视化
例题3.试利用荷载集度、剪力和弯矩间的微分关系作左图所示梁的剪力图和弯矩图。



解题思想与算法:
A.头文件与宏定义、全局变量声明部分:
#include<stdio.h>
#include<math.h>
#define N 5
double M[N];//外力偶矩
double F[N];//均匀集中力
double f[N];//分布力
double l[N-1];//各段长度
double L=0.0;//总长
double Fs;//总力
double Ms;//总力偶矩
double x=0.0;
int Number;
double F_Data;
double M_Data;
B.主函数与外部函数部分:
(1).按照提示输入对应数据.
按受力情况来分,左图的梁可分为AC与CB两段,在程序中,字母标记方式仍为:以O为原点,按照分段情况依次标记A、B、C等字母,如右图所示,OA对应AC段,AB对应CB段,基于![]() =0与
=0与![]() =0原理求解
=0原理求解![]() ,由
,由![]() ﹒2m-2kN﹒1.5m=0可得
﹒2m-2kN﹒1.5m=0可得![]() =1.5kN。按要求界面提示输入对应参数。
=1.5kN。按要求界面提示输入对应参数。
运行界面:

代码片段:
int main(){
char Letter[N]={'O','A','B','C','D'};
printf("请输入所分段数(<=4):");
scanf("%d",&Number);
printf("请按一定方向依次输入连续各段长度与分布力情况.格式:长度,分布力(用英文逗号隔开).\n");
for(int i=0;i<Number;i++){
printf("%c%c段:",Letter[i],Letter[i+1]);
scanf("%lf,%lf",&l[i],&f[i]);
}
printf("请输入各点受集中力与外力偶矩(以顺时针为正)情况.格式:集中力,外力偶矩(用英文逗号隔开).\n");
for(int i=0;i<Number;i++){
printf("%c点:",Letter[i]);
scanf("%lf,%lf",&F[i],&M[i]);
}
(2).程序计算剪应力:分布力(斜率)*距离+集中力(常数);计算弯矩:剪应力的积分+外力偶矩(常数)。将用户输入的每段距离分为20等份(也可以根据用户需要分为若干等份),创建名为“弯曲应力数据”的Excel表格,将坐标x、剪应力、弯矩数据分别导入表格1~3列。程序界面不会输出任何计算结果,程序结束。
代码片段:
FILE *fp;
fp=fopen("弯曲应力数据.xls","w");//建立“弯曲应力数据”Excel文件
fprintf(fp,"x\tFs\tM\n");//在文件中输入对应参数名
fprintf(fp,"0\t0\t0\n");//图像的闭合性,Fs从零开始
for(int i=0;i<Number;i++)Ms=M[i]+Ms;
for(int i=0;i<Number;i++){
if(i<1){Fs=F[0];}
else{Fs=Fs+F[i];}
fprintf(fp,"%lf\t%lf\t%lf\n",x,Fs,Ms);
for(int j=0;j<20;j++){//各段取20等份,计算对应x坐标的数据
x=x+l[i]/20;
if(i<1){F_Data=f[i]*x+F[i];
M_Data=0.5*f[i]*x*x+F[i]*x+Ms;
}
else{F_Data=f[i]*(x-L)+Fs;
M_Data=0.5*f[i]*(x-L)*(x-L)+Fs*(x-L)+Ms;
}
fprintf(fp,"%lf\t%lf\t%lf\n",x,F_Data,M_Data);
}
if(i<1){Fs=f[i]*l[i]+F[i];
Ms=0.5*f[i]*l[i]*l[i]+F[i]*l[i]+Ms;
}
else{Ms=0.5*f[i]*l[i]*l[i]+Fs*l[i]+Ms;
Fs=f[i]*l[i]+Fs;
}
L=L+l[i];
fprintf(fp,"%lf\t%lf\t%lf\n",L,Fs,Ms);
}
fprintf(fp,"%lf\t0\t%lf\n",L,Ms);
fclose(fp);//保存并关闭文件
return 0;
}
(3).用Excel处理数据:打开Excel后,点击“插入”,点击图表并选择散点图,选择一种合适的图表样式,如果不想被过多数据点干扰可选择“带平滑线的散点图”。例如,可得到如下图所示的剪力图与弯矩图,蓝线与x轴包围的部分表示剪力图,橙线与x轴包围的部分表示弯矩图。另外,还可以通过显示坐标数据等功能找出对应的极值点,进一步处理数据。

Part 2.弯曲应力可视化程序的应用
变式5.由工字形钢制成的简支梁受力如图所示。已知材料的许用弯曲正应力[σ]=170MPa,许用切应力![]() =100MPa。试选择工字钢号码。
=100MPa。试选择工字钢号码。

解题思路:对A点约束反力进行分析,基于![]() =0与
=0与![]() =0原理求解得:约束反力FA=113.12kN。按照界面提示输入参数,打开程序生成的Excel表格,插入图表,找到扭矩图曲线对应的最高点(极大值点),选择显示其对应纵轴坐标,得到Mmax约为83.97kN﹒m。最后按照题目要求进行计算,得出结果。
=0原理求解得:约束反力FA=113.12kN。按照界面提示输入参数,打开程序生成的Excel表格,插入图表,找到扭矩图曲线对应的最高点(极大值点),选择显示其对应纵轴坐标,得到Mmax约为83.97kN﹒m。最后按照题目要求进行计算,得出结果。
运行界面:

Excel处理结果:

结论:
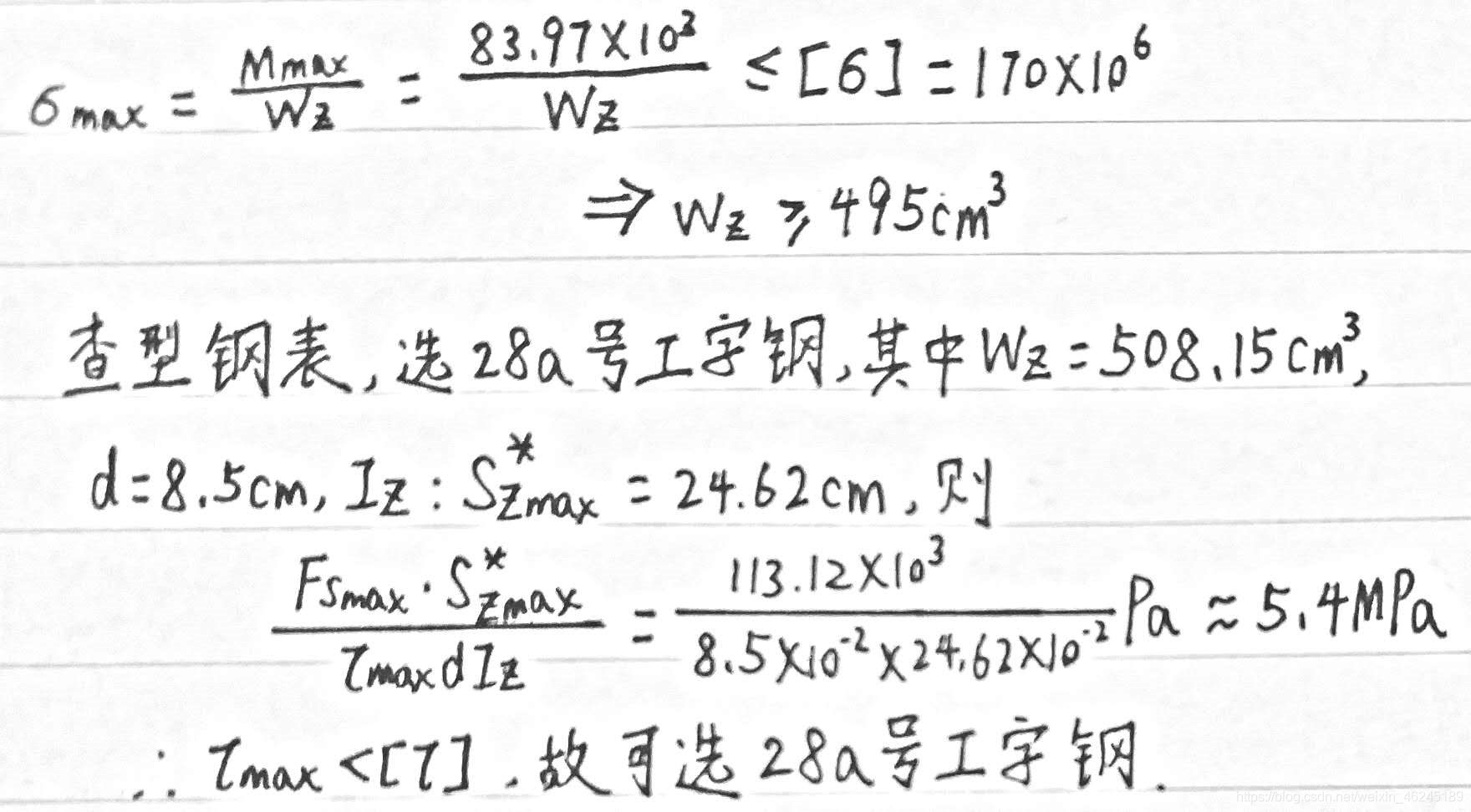
弯曲应力篇对简单力学模型的剪力图、弯矩图实现了可视化的效果,使用支持MATLAB、Python等语言的IDE也能更方便地实现这种效果。最后一篇blog会对扭转变形、拉压变形、弯曲应力几篇内容进行总结,欢迎继续阅读QAQ~
























 2446
2446

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








