ADAPTIVE LEARNING RATE
在训练过程中Critical Point 不一定是我们训练过程中最大的阻碍,当Loss不再下降时,我们的Gradient不一定很小。例如下图,还在Error Surface的两个谷壁反复震荡。

当我们给训练设置同样的Learning Rate 会出现下面的情况:
1 Learning Rate = ,步幅大,反复横跳;(左下图)
2 Learning Rate = , 步幅小,起初训练正常,随后无法逼近Local Minima;(右下图)
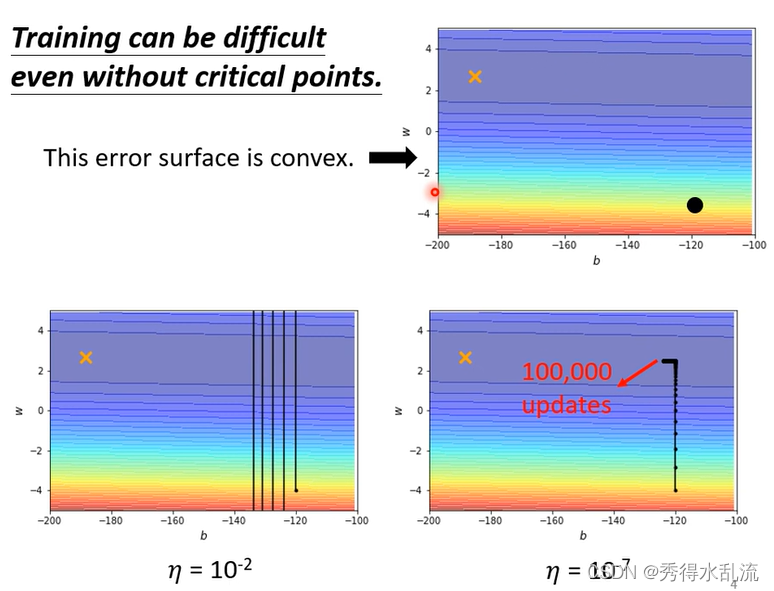
我们需要更好的Gradient Descend方法,为每一个Learning Rate参数定制化,我们的原则是如果Gradient大,我们希望此时Learning Rate小一点,反之我们可以让Learning Rate 大一点。
ROOT MEAN SQUARE
于是我们使用Root Mean Square,如下图所示,它也被用在Adagrad中。

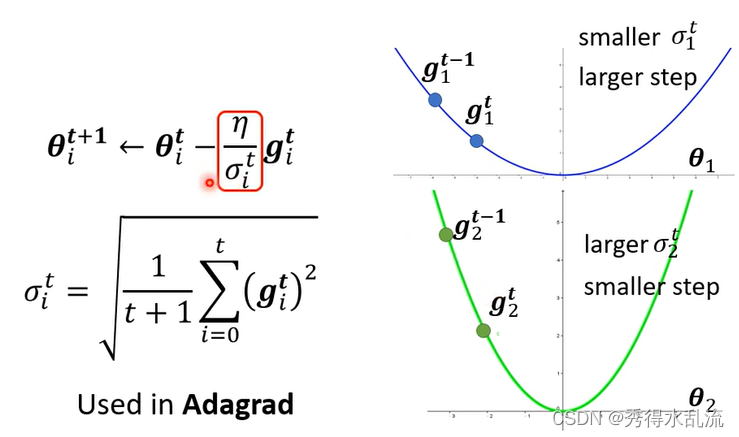
由于即使是同一个参数,它Learning Rate 也会随着时间而改变,我们接着引入新的方法。
RMSProp
在这个方法中,新增了一个参数,如果
接近0,代表刚算出来的gi相较于之前算出的gradient 比较重要,如果
接近1 ,代表现在算出来的 gi相对不重要,而之前的算出来的gradient比较重要。它是一个超参数。

目前较好的Adam方法,就是将RMSProp和Momentum结合一起使用。

Learning Rate Scheduling:让 η 与时间有关
Learning Rate Decay:随着时间增加让 η 越来越小,因为随着时间增加越更新离目标点越接近。
Warm Up:随着时间 η先增大,后减小。

Optimization Summary:
最后针对基础的Gradient Desecent有三个地方进行优化。
1 Momentum:它考虑了过去所有的Gradient而非眼前,并且考虑方向;
2 Learning Rate Scheduling:常用的Warm Up能很好提高性能;
3 RMS:Root Mean Square Prop,可以手动设置来调整 ,针对过去的Gradient,但不考虑其方向,只考虑大小;

LOSS FUNCTION
在Classification中,可以用MSE和Cross-Entropy两种Loss function,但是他们是不同的。

Soft-Max:

在分类问题中,选用Cross-Entropy是明显优于MSE的,由下面例子可知,如果使用MSE在Loss很大的时候,仍然会产生Stuck,导致训练终止。而此时Cross-entropy是表现优的。
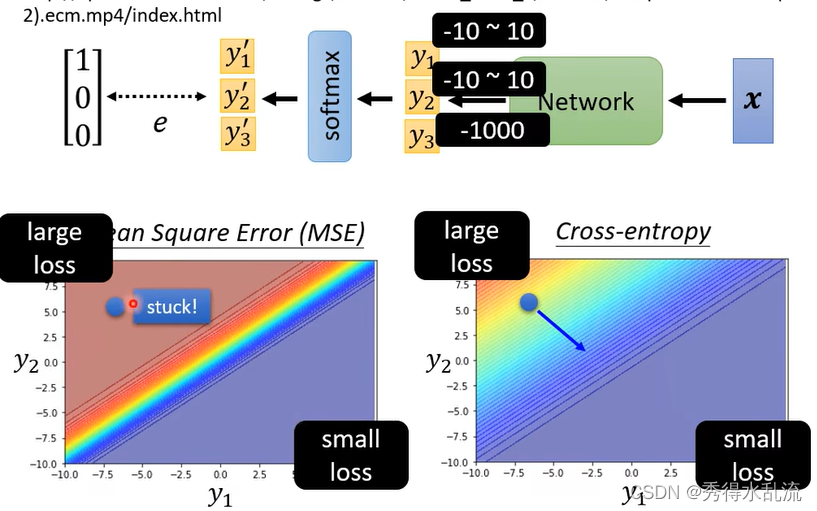
所以对Loss Function的选择也会影响Optimization的过程。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








