迟到的Day2-CSDN博客

本文链接：https://blog.csdn.net/weixin_46275604/article/details/143466445

day2

lc209 长度最小的子数组

> 给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。 > > 示例： > > + 输入：s = 7, nums = [2,3,1,2,4,3] > + 输出：2 > + 解释：子数组 [4,3] 是该条件下的长度最小的子数组。 >

暴力解法:

两个for循环, 不断地找符合条件的子数组,但是时间复杂度是O(n^2) 但是在最后leetcode跟新了数据这种很明显超时了.

滑动窗口(双指针):

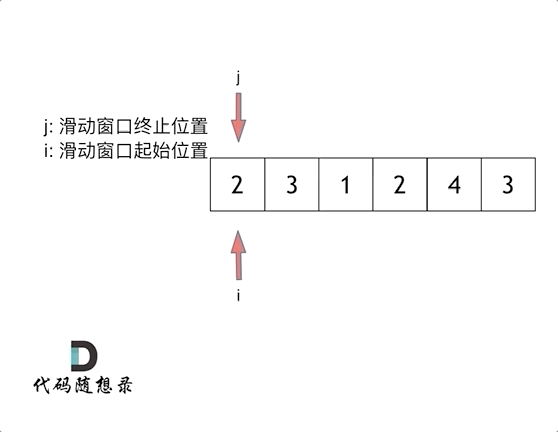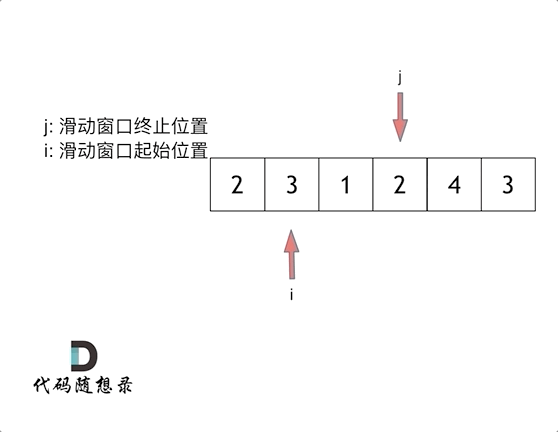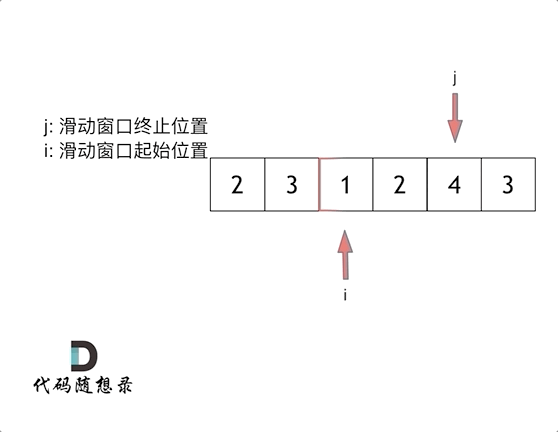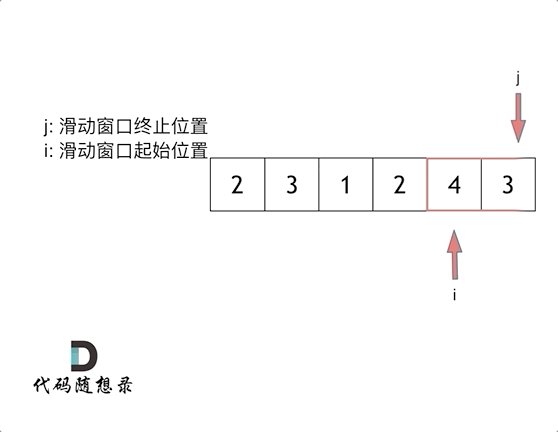
滑动窗口就是不断的调整子序列的起点和终点直到得出想要的结果

俩指针

i 起点 j 终点起点和终点最开始都在数组的第一个元素位置

先固定i 移动j 直到找到满足sum 满足了就停止j终点

此时移动i起点找到最短满足的如果出现小于目标值的情况那么固定i j继续移动

public int minSubArrayLen(int s, int[] nums){

    int l = 0, sum = 0, res = Integer.MAX_VALUE;

    for(int r = 0; r < nums.length; r++){
        sum += nums[r];
        while(sum >= s){
            res = Math.min(res, r - l + 1);
            sum -= nums[l++];
        }
    }
    return res == Integer.MAX_VALUE ? 0 : res;
}

lc59螺旋矩阵I

> 给你一个正整数 ` n` ，生成一个包含 ` 1` 到 ` n ²` 所有元素，且元素按顺时针顺序螺旋排列的 ` n x n` 正方形矩阵 ` matrix` 。 >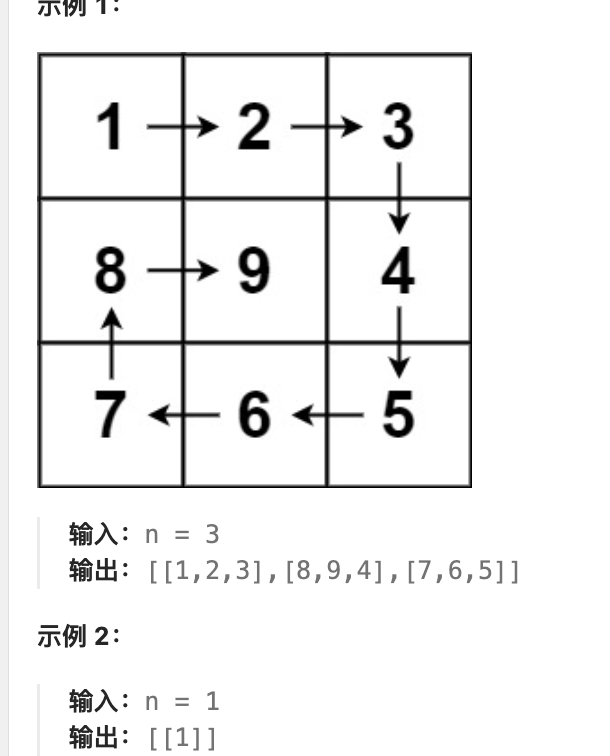

本题关键在于边界条件的处理也就是四方形的四个角怎么处理

遵循一个不变量到底是[ ] 还是[ )

如果[ ) 也就是在便利一条边时候只要边的起点不要边的终点作为下一条的起点

题目输入n n就是代表矩阵的大小比如n = 4 那就返回4*4的矩阵

那么螺旋转圈次数就是n / 2次

如果n是奇数除以2 除不尽剩余一个

因为每一圈的起点都不算固定的所以for循环的i 不可能是固定

 public static int[][] generateMatrix(int n) {
        int[][] arr = new int[n][n];
        int startX = 0, startY = 0, offset = 1,loop = 1,count = 1,x,y;
        while (loop <= n / 2){
            for(y = startY; y < n - offset; y++) arr[startX][y] = count++;
            for(x = startX; x < n - offset; x++) arr[x][y] = count++;
            for( ; y > startY; y--) arr[x][y] = count++;
            for( ; x > startX; x--) arr[x][y] = count++;
            startX++;
            startY++;
            loop++;
            offset++;
        }
        if(n % 2 == 1) arr[startX][startY] = count;
        return arr;
    }

前缀和

> 题目描述 > > 给定一个整数数组 Array，请计算该数组在每个指定区间内元素的总和。 > > 输入描述 > > ** 第一行输入为整数数组 Array 的长度 n，接下来 n 行，每行一个整数，表示数组的元素。随后的输入为需要计算总和的区间，直至文件结束。** > > 输出描述 > > 输出每个指定区间内元素的总和。 >

思路:

暴力解法

有一个区间之后直接暴力把这个区间的和都累加一遍但是提交代码提示超时

前缀和

前缀和就是利用计算过的子数组的和从而降低区间查询需要累加计算的次数

在设计计算区间和时候非常有用

比如要计算vec[i] 在这个数组上的区间和

首先累加 p[i]表示下标0~i的vec累加和

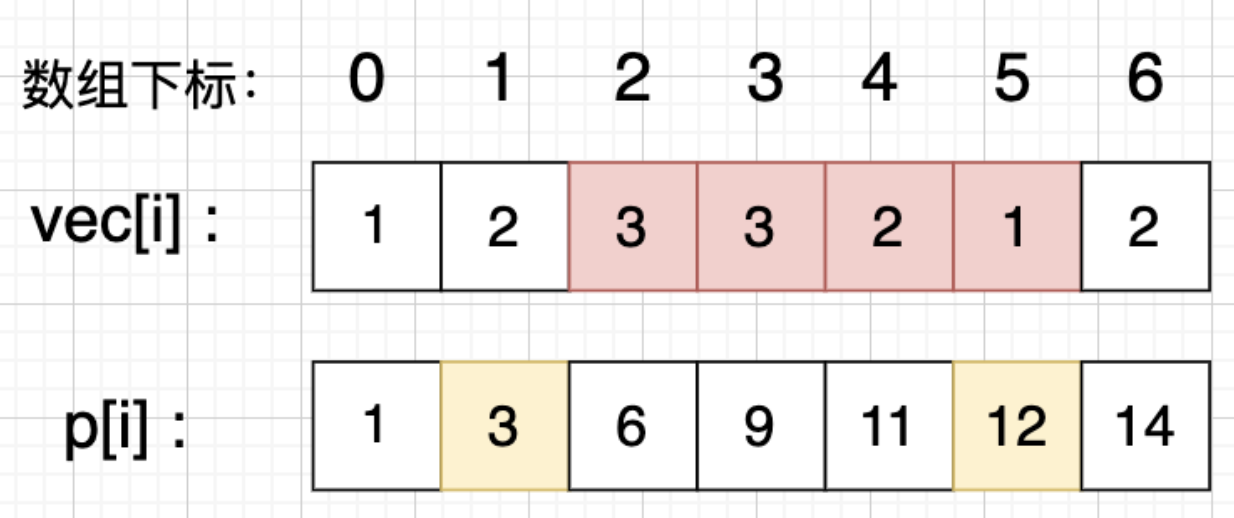
计算下标2到5的区间和

区间下标 [2, 5] 的区间和，那么应该是 p[5] - p[1]，而不是 p[5] - p[2]。

public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[] vec = new int[n]; //原本数组
        int[] p = new int[n];  //原本数组的区间和
        // 计算原本数组的区间和
        int preSum = 0;
        for(int i = 0; i < n; i++){
            vec[i] = sc.nextInt();
            preSum += vec[i];
            p[i] = preSum;
        }
        
        while (sc.hasNextInt()){
            int a = sc.nextInt();
            int b = sc.nextInt();
            int sum = 0;
            if(a == 0) sum = p[b];
            else sum = p[b] - p[a - 1];
            System.out.println(sum);
        }

    }
}

开发商买土地

> 【题目描述】 > > 在一个城市区域内，被划分成了n * m个连续的区块，每个区块都拥有不同的权值，代表着其土地价值。目前，有两家开发公司，A 公司和 B 公司，希望购买这个城市区域的土地。 > > 现在，需要将这个城市区域的所有区块分配给 A 公司和 B 公司。 > > 然而，由于城市规划的限制，只允许将区域按横向或纵向划分成两个子区域，而且每个子区域都必须包含一个或多个区块。 > > 为了确保公平竞争，你需要找到一种分配方式，使得 A 公司和 B 公司各自的子区域内的土地总价值之差最小。 > > 注意：区块不可再分。 >

解法思路:

本题要求任意两行或者两列之间的数值之和, 也就是前缀和

先计算出行列方向的和然后统计好前n行的和 q[n] 如果要求a行到b行之间的总和那么就是q[b] - q[a - 1]

将一个二维数组划分为两部分，使得这两部分的和之差最小。

首先计算整个数组的总和 sum，然后分别求出每一行和每一列的和，存储在 rowSum 和 colSum 数组中。

接着，通过累加 rowSum 数组中的行和，逐步模拟横向划分，将前几行作为一部分、剩余行作为另一部分。每次划分时，计算当前划分后两部分和的差值，并更新最小差值 result。同理，对于纵向划分，累加 colSum 数组中的列和，模拟不同的列划分方式，计算两部分的差值，并更新最小差值。最终输出的 result 就是所有可能划分方式中两部分和的最小差值。

import java.util.*;

public class Main{
    
    public static void main (String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int sum = 0;
        int[][] vec = new int[n][m];
        for(int i = 0; i < n; i++){
            for(int j = 0; j < m; j++){
                vec[i][j] = sc.nextInt();
                sum += vec[i][j];
            }
        }
        
        // 统计每行的和
        int[] rowSum = new int[n];
        for(int i = 0; i < n; i++){
            for(int j = 0; j < m; j++){
                rowSum[i] += vec[i][j];
            }
        }
        
        // 统计每列的和
        int[] colSum = new int[m];
        for(int j = 0; j < m; j++){
            for(int i = 0; i < n; i++){
                colSum[j] += vec[i][j];
            }
        }
        
        int res = Integer.MAX_VALUE;
        
        // 计算行划分的最小差值
        int rowCut = 0;
        for(int i = 0; i < n; i++){
            rowCut += rowSum[i];
            res = Math.min(res, Math.abs(sum - 2 * rowCut));
        }
        
        // 计算列划分的最小差值
        int colCut = 0;
        for(int j = 0; j < m; j++){
            colCut += colSum[j];
            res = Math.min(res, Math.abs(sum - 2 * colCut));
        }
        
        System.out.println(res);
        
        sc.close();
    }
}