P1600 [NOIP2016 提高组] 天天爱跑步

weixin_46304837

于 2021-08-20 14:48:06 发布

阅读量156

点赞数

本文链接：https://blog.csdn.net/weixin_46304837/article/details/119823372

版权

P1600 [NOIP2016 提高组] 天天爱跑步

题目

题目描述

小c 同学认为跑步非常有趣，于是决定制作一款叫做《天天爱跑步》的游戏。《天天爱跑步》是一个养成类游戏，需要玩家每天按时上线,完成打卡任务。

这个游戏的地图可以看作一一棵包含 $n$ 个结点和 $n - 1$ 条边的树，每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从 $1$ 到 $n$ 的连续正整数。

现在有 $m$ 个玩家，第 $i$ 个玩家的起点为 $s_i$ ，终点为 $t_i$ 。每天打卡任务开始时，所有玩家在第 $0$ 秒同时从自己的起点出发，以每秒跑一条边的速度，不间断地沿着最短路径向着自己的终点跑去，跑到终点后该玩家就算完成了打卡任务。 (由于地图是一棵树，所以每个人的路径是唯一的)

小c 想知道游戏的活跃度，所以在每个结点上都放置了一个观察员。在结点 $j$ 的观察员会选择在第 $w_j$ 秒观察玩家，一个玩家能被这个观察员观察到当且仅当该玩家在第 $w_j$ 秒也正好到达了结点 $j$ 。小c 想知道每个观察员会观察到多少人?

注意：我们认为一个玩家到达自己的终点后该玩家就会结束游戏，他不能等待一段时间后再被观察员观察到。即对于把结点 $j$ 作为终点的玩家：若他在第 $w_j$ 秒前到达终点,则在结点 $j$ 的观察员不能观察到该玩家；若他正好在第 $w_j$ 秒到达终点,则在结点 $j$ 的观察员可以观察到这个玩家。

输入格式

第一行有两个整数 $n$ 和 $m$ 。其中 $n$ 代表树的结点数量, 同时也是观察员的数量, $m$ 代表玩家的数量。

接下来 $n - 1$ 行每行两个整数 $u$ 和 $v$ ，表示结点 $u$ 到结点 $v$ 有一条边。

接下来一行 $n$ 个整数，其中第 $j$ 个整数为 $w_j$ , 表示结点 $j$ 出现观察员的时间。

接下来 $m$ 行，每行两个整数 $s_i$ ，和 $t_i$ ，表示一个玩家的起点和终点。

对于所有的数据，保证 $1\leq s_i,t_i\leq n, 0\leq w_j\leq n$ 。

输出格式

输出 $1$ 行 $n$ 个整数，第 $j$ 个整数表示结点 $j$ 的观察员可以观察到多少人。

输入输出样例

输入 #1
6 3
2 3
1 2 
1 4 
4 5 
4 6 
0 2 5 1 2 3 
1 5 
1 3 
2 6 
输出 #1
2 0 0 1 1 1 
输入 #2
5 3 
1 2 
2 3 
2 4 
1 5 
0 1 0 3 0 
3 1 
1 4
5 5 
输出 #2
1 2 1 0 1 
说明/提示

【样例1说明】

对于 $1$ 号点， $w_i=0$ ，故只有起点为 $1$ 号点的玩家才会被观察到，所以玩家 $1$ 和玩家 $2$ 被观察到，共有 $2$ 人被观察到。

对于 $2$ 号点，没有玩家在第 $2$ 秒时在此结点，共 $0$ 人被观察到。

对于 $3$ 号点，没有玩家在第 $5$ 秒时在此结点，共 $0$ 人被观察到。

对于 $4$ 号点，玩家 $1$ 被观察到，共 $1$ 人被观察到。

对于 $5$ 号点，玩家 $1$ 被观察到，共 $1$ 人被观察到。

对于 $6$ 号点，玩家 $3$ 被观察到，共 $1$ 人被观察到。

【子任务】

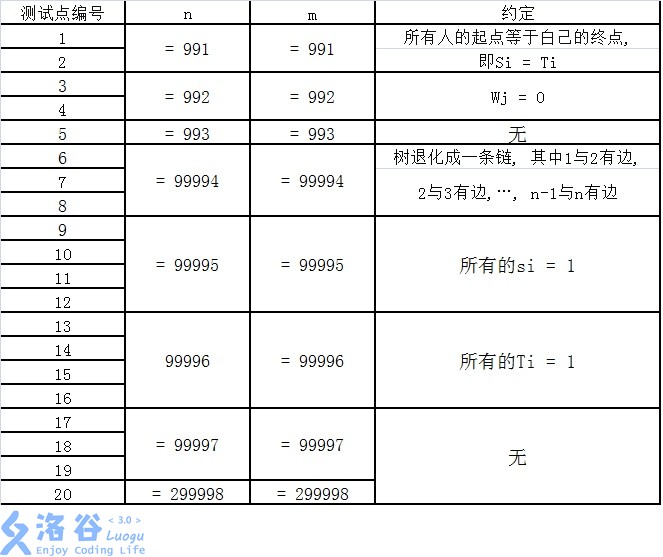
每个测试点的数据规模及特点如下表所示。
提示: 数据范围的个位上的数字可以帮助判断是哪一种数据类型。

思路

part.0问题简化

这里提供一种线段树合并的做法.

我们把一条路径 $s\to t$ 拆开,分为 $s\to lca(s,t)$ 和 $lca(s,t)\to t$ 这两部分.这样相当于一个玩家,只会从低深度跑向高深度或从高深度跑向低深度.

part.1高深度跑向低深度

先考虑 $s\to lca(s,t)$ 这条路径,即高深度跑向低深度.(树上问题中,从子结点到父结点的问题处理起来往往会更简单,因为一个子结点只有一个父结点,一个父结点对应多个子结点)

这条路径什么时候能对一个点 $u$ 产生贡献?

首先, $u$ 得在那条路径上,所以, $u$ 是 $s$ 的祖先结点.

其次 $dist(s,u)=w_u$ 即 $deep(s)-deep(u)=w_u$ , $w_u +de ep(u)=deep(s)$ .( $d i s t$ 表示树上两点距离, $d e e p$ 即深度).

我们采用树上差分:定义数组 $a, b$ .

对于一条路径 $s\to lca(s,t)$ (路径对 $l c a$ 的贡献已经在这里计算,在part.2中就不在计算)
$b_{s,deep(s)}=b_{s,deep(s)}+1\\ b_{father(lca),deep(s)}=b_{father(lca),deep(s)}-1$
对于树上每一个结点 $u$
$a_{u,i}=b_{u,i}+\sum _{v\in son(i)}b_{v,i}$
而 $u$ 点的答案就是 $a_{u,w_u+deep(u)}$ .

代码大概是这样:

void calc1(int u) {
	for(int i = head[u] ; i ; i = ed[i].nxt) {
		int v = ed[i].to;
		if(v == father[u])
			continue;
		calc1(v);
		SegT::root[u] = SegT::merge(SegT::root[u] , SegT::root[v] , 0 , n * 2);
	}
	ans[u] += SegT::query(SegT::root[u] , dep(u) + w[u]);
}

//in main
	for(int i = 1 ; i <= m ; i++)
		s[i] = read() , t[i] = read() , lca[i] = LCA::lca(s[i] , t[i]);
	
	for(int i = 1 ; i <= n ; i++)
		SegT::root[i] = SegT::newnode(0 , n * 2);
	for(int i = 1 ; i <= m ; i++) {//s->lca
		SegT::change(SegT::root[s[i]] , dep(s[i]) , 1);
		SegT::change(SegT::root[father[lca[i]]] , dep(s[i]) , -1);
	}
	calc1(root);

part.2低深度跑向高深度

对于路径 $lca(s,t)\to t$ 是从低深度跑向高深度,如果我们从上到下统计答案,是很麻烦的.如果我们仍用差分,改一下 $l c a$ 的差分数组,整个子树都要受到影响,而不是我们所希望的 $lca(s,t)\to t$ 这条路径.

所以,我们考虑能不能像上面一样,子结点先算出答案,然后合并到父结点,算出父结点的答案.

再看下线段树的change函数:void change(int p , int pos , int dat), $p$ 是当前子树的根节点编号,是不能做什么手脚的了, $d a t$ 是差分的数据,一般只会用1和-1,最有希望能帮我们实现目的的应该是 $p o s$ .

那我们应该如何设计 $p o s$ 呢?

想想part.1中为什么可以? $w_u+deep(u)=deep(s)$ ,这个等式中,左边只跟结点 $u$ 有关,右边只跟结点 $s$ 有关,所以等式左边用于统计答案,右边用于初始化差分数组.

同样的,如果我们在part.2中也找到一个类似的等式,一边只和 $u$ 有关,另一边只和 $s, t, l c a$ 有关,我们的目的就达到了.

应该不难想到有一个这样的等式:
$\text{u到s的路径长度}=deep(u)+deep(s)-2\cdot deep(lca(u,s))=w_u$
又因为 $u$ 在路径 $lca(s,t)\to t$ 上,所以 $l c a (u, s) = l c a (s, t)$ ,同时,移项可以得到:
$w_u-deep(u)=deep(s)-2\cdot deep(lca(s,t))$
为了防止出现负数(如果有负数,在线段树递归左右子树时会出现鬼畜),我们两边同时+n.
$w_u-deep(u)+n=deep(s)-2\cdot deep(lca(s,t))+n$
所以代码就出来啦.

void calc2(int u) {
	for(int i = head[u] ; i ; i = ed[i].nxt) {
		int v = ed[i].to;
		if(v == father[u])
			continue;
		calc2(v);
		SegT::root[u] = SegT::merge(SegT::root[u] , SegT::root[v] , 0 , n * 2);
	}
	ans[u] += SegT::query(SegT::root[u] , w[u] - dep(u) + n);
}
//in main
	SegT::clear();//清空线段树
	for(int i = 1 ; i <= n ; i++)
		SegT::root[i] = SegT::newnode(0 , n * 2);
	for(int i = 1 ; i <= m ; i++) {//lca->t
		SegT::change(SegT::root[t[i]] , dep(s[i]) - 2 * dep(lca[i]) + n , 1);
		SegT::change(SegT::root[lca[i]] , dep(s[i]) - 2 * dep(lca[i]) + n , -1);
	}
	
	calc2(root);

代码

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
using namespace std;
int read() {
	int re = 0;
	char c = getchar();
	bool negt = false;
	while(c < '0' || c > '9')
		negt |= (c == '-') , c = getchar();
	while(c >= '0' && c <= '9')
		re = (re << 1) + (re << 3) + c - '0' , c = getchar();
	return negt ? -re : re;
}

const int N = 300010;
const int maxZ = 100000;
const int M = 300010;
const int M_logZ = M * 20;

struct EDGE {
	int to , nxt;
} ed[N * 2];
int head[N];
void addedge(int u , int v) {
	static int cnt;
	++cnt;
	ed[cnt].to = v , ed[cnt].nxt = head[u] , head[u] = cnt;
}

int n , m , root;

int father[N];
namespace LCA {//RMQ-LCA
	int cnt = 0;
	int dep[N * 2] , id[N * 2] , first[N];
	int st[N * 4][25];
	void dfs(int u , int nowdep) {
		++cnt;
		id[cnt] = u , dep[cnt] = nowdep , first[u] = cnt;
		for(int i = head[u] ; i ; i = ed[i].nxt) {
			int v = ed[i].to;
			if(v == father[u])
				continue;
			father[v] = u;
			dfs(v , nowdep + 1);
			++cnt;
			id[cnt] = u , dep[cnt] = nowdep;
		}
	}
	void init(int root) {
		dfs(root , 1);

		for(int i = 1 ; i <= cnt ; i++)
			st[i][0] = i;
		int k = log(n) / log(2) + 1;
		dep[0] = 0x3fffffff;
		for(int j = 1 ; j <= k ; j++)
			for(int i = 1 ; i <= cnt ; i++)
				st[i][j] = dep[st[i][j - 1]] < dep[st[i + (1 << j - 1)][j - 1] ] ? st[i][j - 1] : st[i + (1 << j - 1)][j - 1];

	}
	int lca(int u , int v) {
		u = first[u] , v = first[v];
		if(u > v) {
			int tmp;
			tmp = u , u = v , v = tmp;
		}
		int k = log(v - u + 1) / log(2);
		return id[
		           dep[st[u][k]] < dep[st[v - (1 << k) + 1][k]] ? st[u][k] : st[v - (1 << k) + 1][k]
		       ];
	}
}
inline int dep(int u) {
	return LCA::dep[LCA::first[u]];
}


const int M_logN = M * 20;
namespace SegT {//线段树,带合并
	int root[N];
	struct NodeClass {
		int l , r , ls , rs , dat;
	} node[M_logN];
	inline int newnode(int l , int r) {
		static int cnt = 0;
		if(l == -1 && r == -1) {
			cnt = 0;
			return 0;
		}
		++cnt;
		node[cnt].l = l , node[cnt].r = r , node[cnt].dat = 0;
		return cnt;
	}
	void change(int p , int pos , int dat) {
		if(node[p].l == node[p].r)
			node[p].dat += dat;
		else {
			int l = node[p].l , r = node[p].r;
			int mid = (l + r) / 2;
			if(l + r < 0)	--mid;
			if(pos <= mid)
				change(node[p].ls = (node[p].ls == 0 ? newnode(l , mid) : node[p].ls) , pos , dat);
			else 
				change(node[p].rs = (node[p].rs == 0 ? newnode(mid + 1 , r) : node[p].rs) , pos , dat);
		}
	}
	int query(int p , int pos) {
		if(p == 0)
			return 0;
		if(node[p].l == node[p].r)
			return node[p].dat;
		int mid = (node[p].l + node[p].r) / 2;
		if(node[p].l + node[p].r < 0)--mid;
		if(pos <= mid)
			query(node[p].ls , pos);
		else
			query(node[p].rs , pos);
	}
	int merge(int p1 , int p2 , int l , int r) {
		if(p1 == 0 || p2 == 0)
			return p1 == 0 ? p2 : p1;
		if(l == r) {
			node[p1].dat += node[p2].dat;
			return p1;
		}
		int mid = (l + r) / 2;
		if(l + r < 0)--mid;
		node[p1].ls = merge(node[p1].ls , node[p2].ls , l , mid);
		node[p1].rs = merge(node[p1].rs , node[p2].rs , mid + 1 , r);
		return p1;
	}
	
	void clear() {
		memset(root , 0 , sizeof(root));
		memset(node , 0 , sizeof(node));
		newnode(-1 , -1);
	}
}

int ans[N];


int s[N] , t[N] , lca[N];
int w[N];

void calc1(int u) {
	for(int i = head[u] ; i ; i = ed[i].nxt) {
		int v = ed[i].to;
		if(v == father[u])
			continue;
		calc1(v);
		SegT::root[u] = SegT::merge(SegT::root[u] , SegT::root[v] , 0 , n * 2);
	}
	ans[u] += SegT::query(SegT::root[u] , dep(u) + w[u]);
}


void calc2(int u) {
	for(int i = head[u] ; i ; i = ed[i].nxt) {
		int v = ed[i].to;
		if(v == father[u])
			continue;
		calc2(v);
		SegT::root[u] = SegT::merge(SegT::root[u] , SegT::root[v] , 0 , n * 2);
	}
	ans[u] += SegT::query(SegT::root[u] , w[u] - dep(u) + n);
}
int main() {
	
	n = read() , m = read() , root = 1;
	for(int i = 1 ; i < n ; i++) {
		int u = read() , v = read();
		addedge(u , v) , addedge(v , u);
	}
	
	LCA::init(root);
	for(int i = 1 ; i <= n ; i++)
		w[i] = read();
	for(int i = 1 ; i <= m ; i++)
		s[i] = read() , t[i] = read() , lca[i] = LCA::lca(s[i] , t[i]);
	
	for(int i = 1 ; i <= n ; i++)
		SegT::root[i] = SegT::newnode(0 , n * 2);
	for(int i = 1 ; i <= m ; i++) {//s->lca
		SegT::change(SegT::root[s[i]] , dep(s[i]) , 1);
		SegT::change(SegT::root[father[lca[i]]] , dep(s[i]) , -1);
	}
	calc1(root);
	
	
	SegT::clear();
	for(int i = 1 ; i <= n ; i++)
		SegT::root[i] = SegT::newnode(0 , n * 2);
	for(int i = 1 ; i <= m ; i++) {//lca->t
		SegT::change(SegT::root[t[i]] , dep(s[i]) - 2 * dep(lca[i]) + n , 1);//+n,防止区间包含负数时出现鬼畜
		SegT::change(SegT::root[lca[i]] , dep(s[i]) - 2 * dep(lca[i]) + n , -1);
	}
	
	calc2(root);
	
	for(int i = 1 ; i <= n ; i++)
		printf("%d " , ans[i]);
	return 0;
}

weixin_46304837

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
P1600 [NOIP2016 提高组] 天天爱跑步

P1600 [NOIP2016 提高组] 天天爱跑步题目题目描述小c 同学认为跑步非常有趣，于是决定制作一款叫做《天天爱跑步》的游戏。《天天爱跑步》是一个养成类游戏，需要玩家每天按时上线,完成打卡任务。这个游戏的地图可以看作一一棵包含 nnn 个结点和 n−1n-1n−1 条边的树，每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从 111 到 nnn 的连续正整数。现在有 mmm 个玩家，第 iii 个玩家的起点为 sis_isi，终点为 tit_iti。每天打卡任务
复制链接

扫一扫