一.题目
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
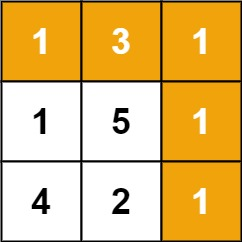
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100
来源:力扣(LeetCode)
链接:题目来源
二.分析
(1)我们要记录走过的路径长度,可以建立一个二维数组dp,我们用 dp[i][j] 来记录到该位置的最短路径长度。因为它只能向下或向右移动一步,所以最上面一行以及最左边一列的记录只需要将它的左边的值/上面的值加入即可。
(2)对于其他位置的值我们要考虑它左边以及上面的值,选择较小的一个加入该位置,最后输出dp数组的最后一个数。
(3)状态转移方程: dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + grid[i][j];
三.代码
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m=grid.size();
int n=grid[0].size();
vector<vector<int>>dp(m,vector<int>(n));
dp[0][0]=grid[0][0];
for(int i=1;i<m;i++)
dp[i][0]=grid[i][0]+dp[i-1][0];
for(int i=1;i<n;i++)
dp[0][i]=grid[0][i]+dp[0][i-1];
for(int i=1;i<m;i++)
{
for(int j=1;j<n;j++)
{
dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j];
}
}
return dp[m-1][n-1];
}
};























 1701
1701











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










