【机器学习基石】线性回归（九）

---

写在前面

本节主要介绍了线性回归原理以及它的可行性，最后与前面学过的线性分类进行了对比分析。

---

1. 线性回归问题

$\bullet$ 引入：我们假设现在有些用户已经申请到了信用卡，但是银行决定给他们发放多少钱。此时返回的结果就是一个实数区间。

$\bullet$ 实现：

$▹$ 现在我们有用户的信息，包括以下内容：年龄、年收入、工作年龄、当前负债。

$▹$ 我们还是像（二）中感知机模型提到的一样，为每一个维度分配一个权重，然后求得总和，最后在减去一个偏差（阈值）。为了优化，把这个偏差放到了第0维度。（具体实现看机器学习基石二中第一块内容）

所以当有d个维度时，自变量 $x=(x_0,x_1,...x_d)$，返回值 $$y\approx \sum _{i=0}^d{w}_i{x}_i$$
线性回归假设：$h(x)=w^{T}x$

（它很像感知机模型，但是感知机模型最终求的是符号）

$▹$ 当 $x$ 只有一个维度或者两个维度时，做出来的直线如下：

对于一维、二维的 $x$ 来说，线性回归最终要找到的就是误差最小的直线以及平面。每个点到直线或者平面的竖直距离就是该点的误差。

$▹$ 计算误差的方法：最小二乘法。我们求解误差的平方和对应的权重，对于单点来说就是：
$$err(\hat{y},y)=(\hat{y}-y{)}^2$$
对于样本数据来说，计算方法为（选择对应误差最小的一组权重值）：
$$E_{in}(w)=\frac{1}{N}\sum _{n=1}^N(w^T{x}_n-y_n{)}^2$$
对于整体数据来说，计算方法为（整体数据对应的误差结果）：
$$E_{out}(w)=\underset{(x,y)\sim P}{\epsilon }(w^{T}x-y{)}^2$$

我们接下来需要实现的就是如何找到较小的 $E_{in}(w)$。

---

2. 求解最小的 $E_{in}(w)$ 对应的 $w$

$\bullet$上面我们已经得到了 $E_{in}(w)$ 的计算方法，接着我们对其进行转换：
$$\begin{array}{cccc}{E}_{in}(w)& =& \frac{1}{N}{\sum }_{n=1}^N(w^T{x}_n-y_n{)}^2=& \frac{1}{N}{\sum }_{n=1}^N(x_n^{T}w-y_n{)}^2\\ & =& \frac{1}{N}{\Vert \begin{array}{c}{x}_1^{T}w-y_1\\ x_2^{T}w-y_2\\ ...\\ x_n^{T}w-y_n\end{array}\Vert }^2& \\ & =& \frac{1}{N}{\Vert \begin{array}{c}\left[\begin{array}{ccc}-& x_1^T& -\\ -& x_2^T& -\\ -& ...& -\\ -& x_N^T& -\end{array}\right]w-\left[\begin{array}{c}{y}_1\\ y_2\\ ...\\ y_N\end{array}\right]\end{array}\Vert }^2& \\ & =& \frac{1}{N}\Vert \underset{N\times d+1}{\underbrace{X}}\underset{d+1\times 1}{\underbrace{w}}-\underset{N\times 1}{\underbrace{y}}\Vert & \end{array}$$

我们将其展开为矩阵形式，最后得到的表达式中有矩阵 $X$，它是样本数据矩阵，它有 $N$ 个样本数据，每个样本数据有 $d$ 维，再加上第0维，一共 $d+1$ 维；向量 $w$ 为权重向量，本来是 $d$ 维，再加上第0维，一共 $d+1$ 维；向量 $y$ 为线性回归直线上对应的值，为 $N$ 行1列。

$\bullet$ 那么先在要求的就是：$$\underset{w}{\min }{E}_{in}(w)=\frac{1}{N}{\Vert Xw-y\Vert }^2$$
其中矩阵 $X$ 和向量 $y$ 都是已知的，那么我们现在做出 $w$ 与 $E_{in}(w)$ 的坐标图：

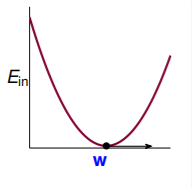
我们要寻找 $w$ 的值，使得 $E_{in}$ 的函数值最小，表现在梯度为0上。

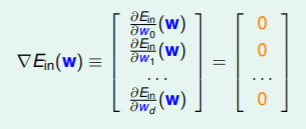
$\bullet$ 将上式展开可得：
$$E_{in}(w)=\frac{1}{N}(w^T\underset{A}{\underbrace{X^{T}X}}w-2w^T\underset{b}{\underbrace{X^{T}y}}+\underset{c}{\underbrace{y^{T}y}})$$
它的梯度为：
$$\nabla E_{in}(w)=\frac{2}{N}(X^{T}Xw-X^{T}y)$$
令偏导等于0，可以得到解为(最终权重向量)：
$$w_{LIN}=(X^{T}X{)}^{-1}{X}^{T}y$$
我们把 $(X^{T}X{)}^{-1}{X}^T$ 叫做伪逆矩阵（pseudo-inverse），记作$X^{†}$，所以有：
$$w_{LIN}=X^{†}y$$
当 $N$ 远大于 $d+1$时，可以求得伪逆矩阵。当我们得到 $w_{LIN}$ 以后，那么线性回归直线就为：
$$\hat{y}=w_{LIN}^T{x}_n=X{X}^{†}y$$

---

3. 泛化问题

$\bullet$ 通过上面推出来的公式我们可以直接得到 $w_{LIN}$，感觉就没有机器自己学习进步的过程，那么是不是就以为着此类方法不属于机器学习呢？

其实在实现的过程中也对 $E_{in}$ 和 $E_{out}$ 进行了最小化的求解，从结果来看，确实属于机器学习。

$\bullet$ 下面通过一种方法来证明线性回归可以得到较好的 $E_{in}$ 和 $E_{out}$。
$$E_{in}(w_{LIN})=\frac{1}{N}{\Vert y-\hat{y}\Vert }^2=\frac{1}{N}{\Vert y-X{X}^{†}y\Vert }^2=\frac{1}{N}\Vert (I-X{X}^{†})y\Vert$$
我们把 $X{X}^{†}$ 叫做帽子矩阵(hat matrix) $H$，下面具体来具体 $H$ 的具体含义（在N维实例中）：

$▹$ $\hat{y}=X{w}_{LIN}$ 位于 $d+1$ 维平面的一条直线。

$▹$ 那么 $y-\hat{y}$ 就是将y向量投影在 $\hat{y}$ 平面时结果最小。

$▹$ 机器学习就是想找到最接近y的直线 $\hat{y}$。记录 $trace(I-H)=N-(d+1)$，$trace(I-H)$ 为 $I-H$ 的迹。

当存在 $noise$ 时，发生改变：

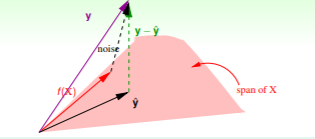
$$E_{in}()w_{LIN}=\frac{1}{N}{\Vert (I-H)noise\Vert }^2=\frac{1}{N}(N-(d+1)){\Vert noise\Vert }^2$$
最后可以分别求得 $\overline{E_{in}}$ 和 $\overline{E_{out}}$：
$$\overline{E_{in}}=noiselevel\cdot (1-\frac{d+1}{N})$$$$\overline{E_{out}}=noiselevel\cdot (1+\frac{d+1}{N})$$

将它们画出来如下：

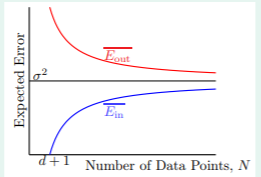
其中 ${\sigma }^2$ 就是 $noiselevel$，当 $N$ 趋于无穷大时，我们可以看到 $\overline{E_{in}}$ 和 $\overline{E_{out}}$ 逐渐接近 $noiselevel$，也证明了这种方式时可以进行机器学习的。

---

4. 与线性分类的对比

可以发现它们的结果 $y$ 定义域不同，线性分类只能为-1或+1，线性回归为整个实数域；$h(x)$ 也不同，线性分类只要符号，线性回归需要具体的值；它们计算误差的方法也不同。

下面给出了两种错误的比较：

可以发现无论在什么情况下，线性分类的误差都不大于线性回归的误差。而且线性回归的方法同样也可以求解线性分类的问题。