周报-240705

本周主要进行了深度学习所需环境的安装，以及深度学习内容的学习

学习内容

1、安装环境

2、动手学深度学习  2.1-2.5

学习时间

2024.7.1——2024.7.5

学习笔记

安装环境

1 安装CUDA

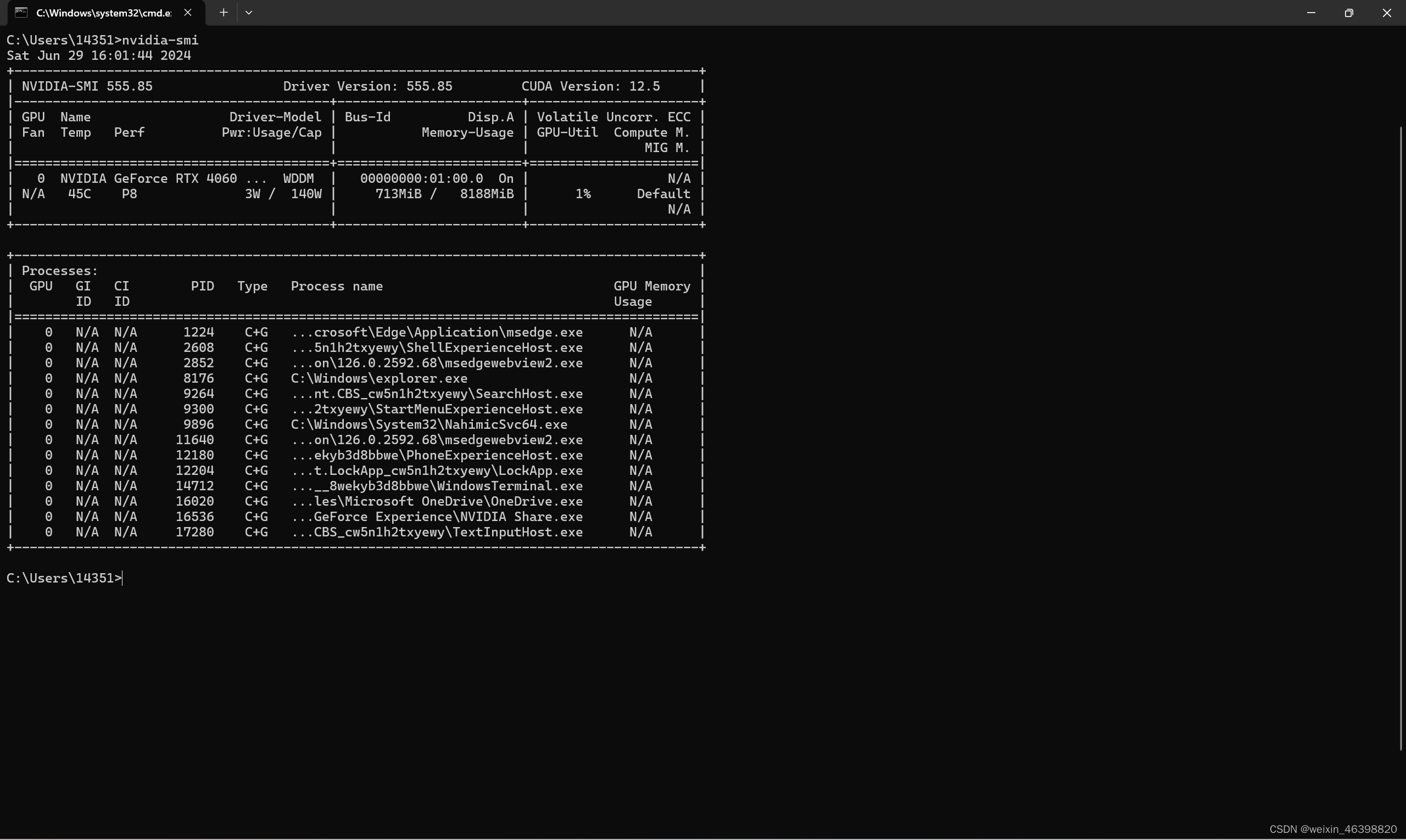
2 安装miniconda

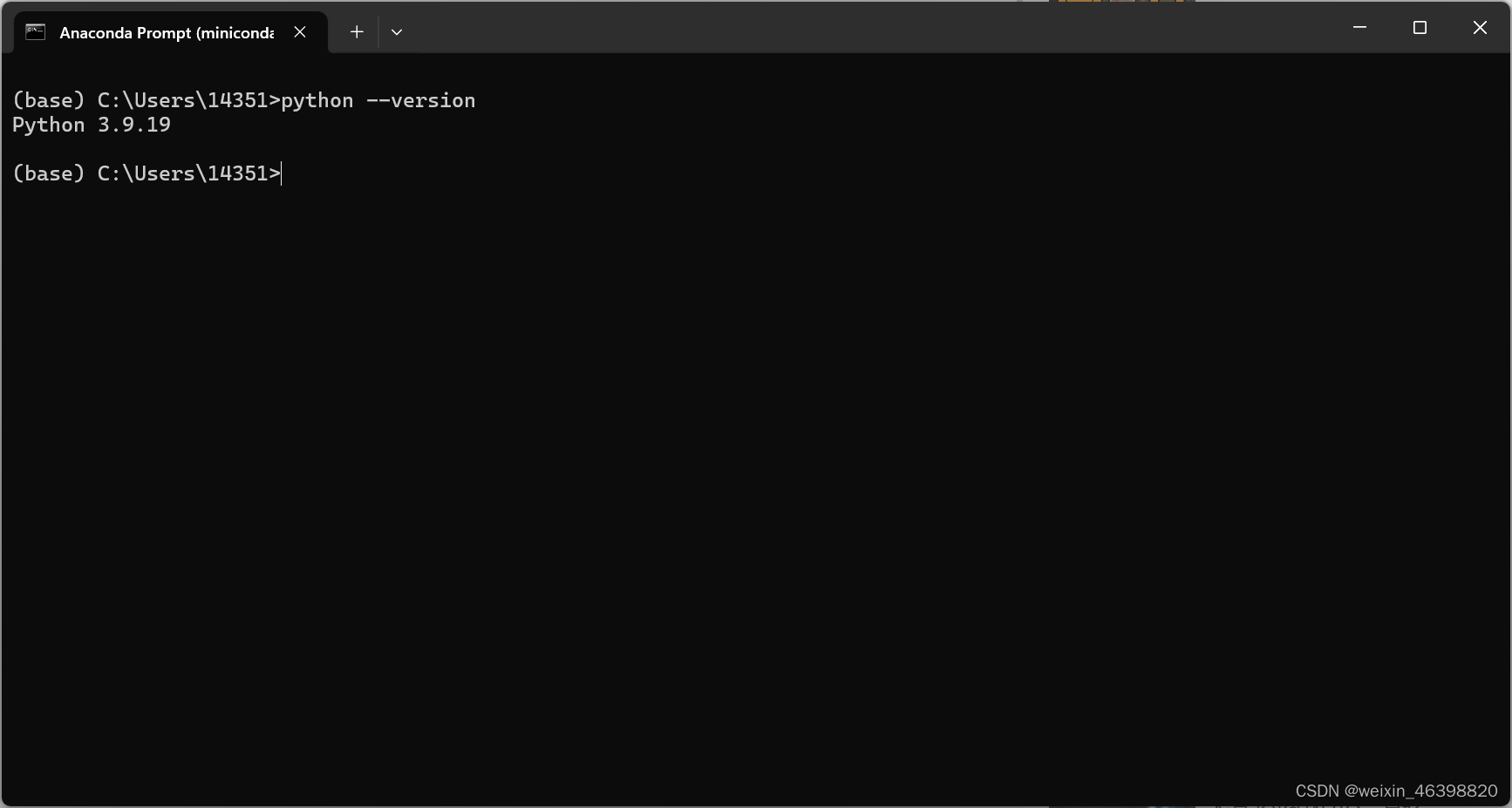
3 安装GPU版Pytorch

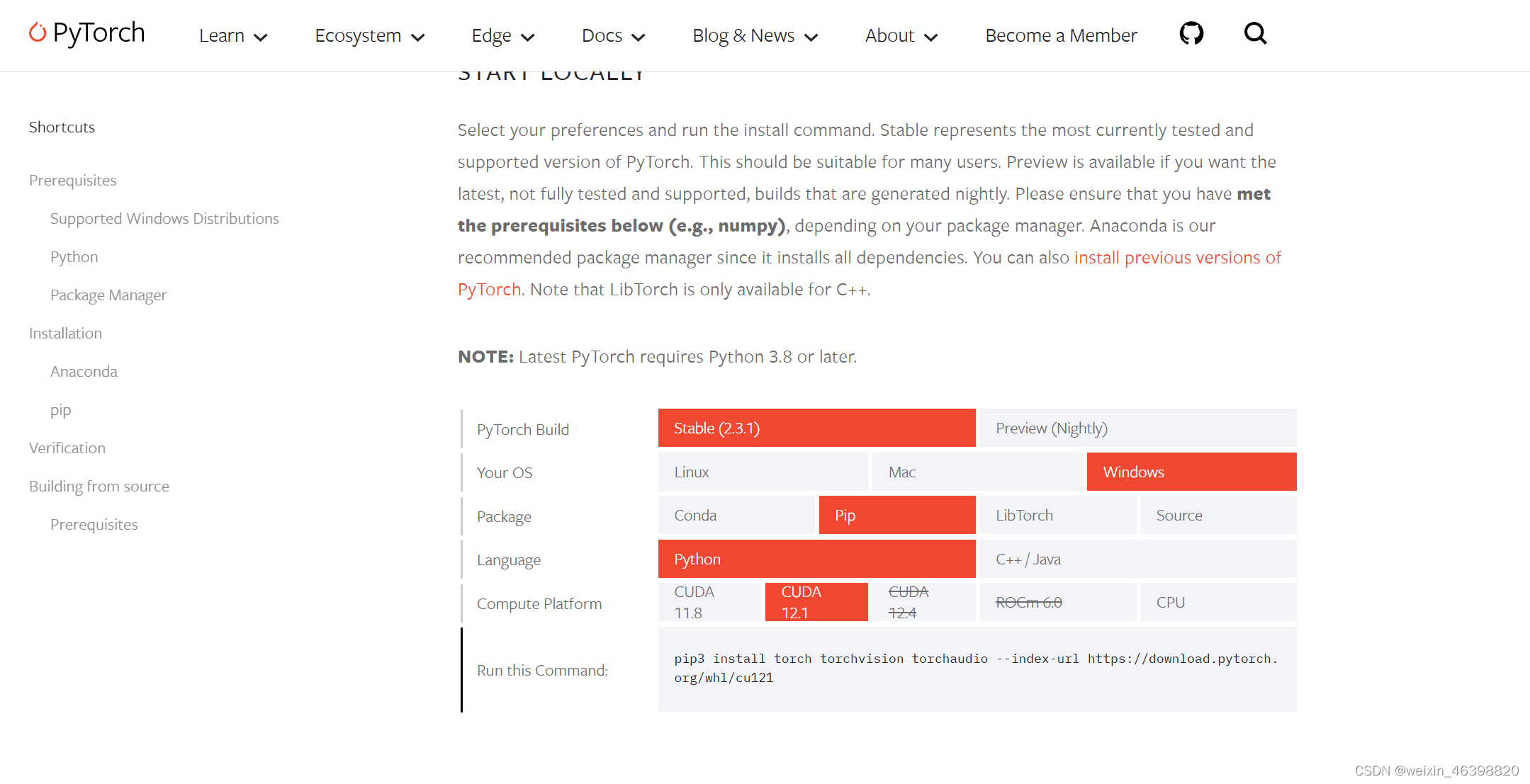
4 安装d2l和Jupyter

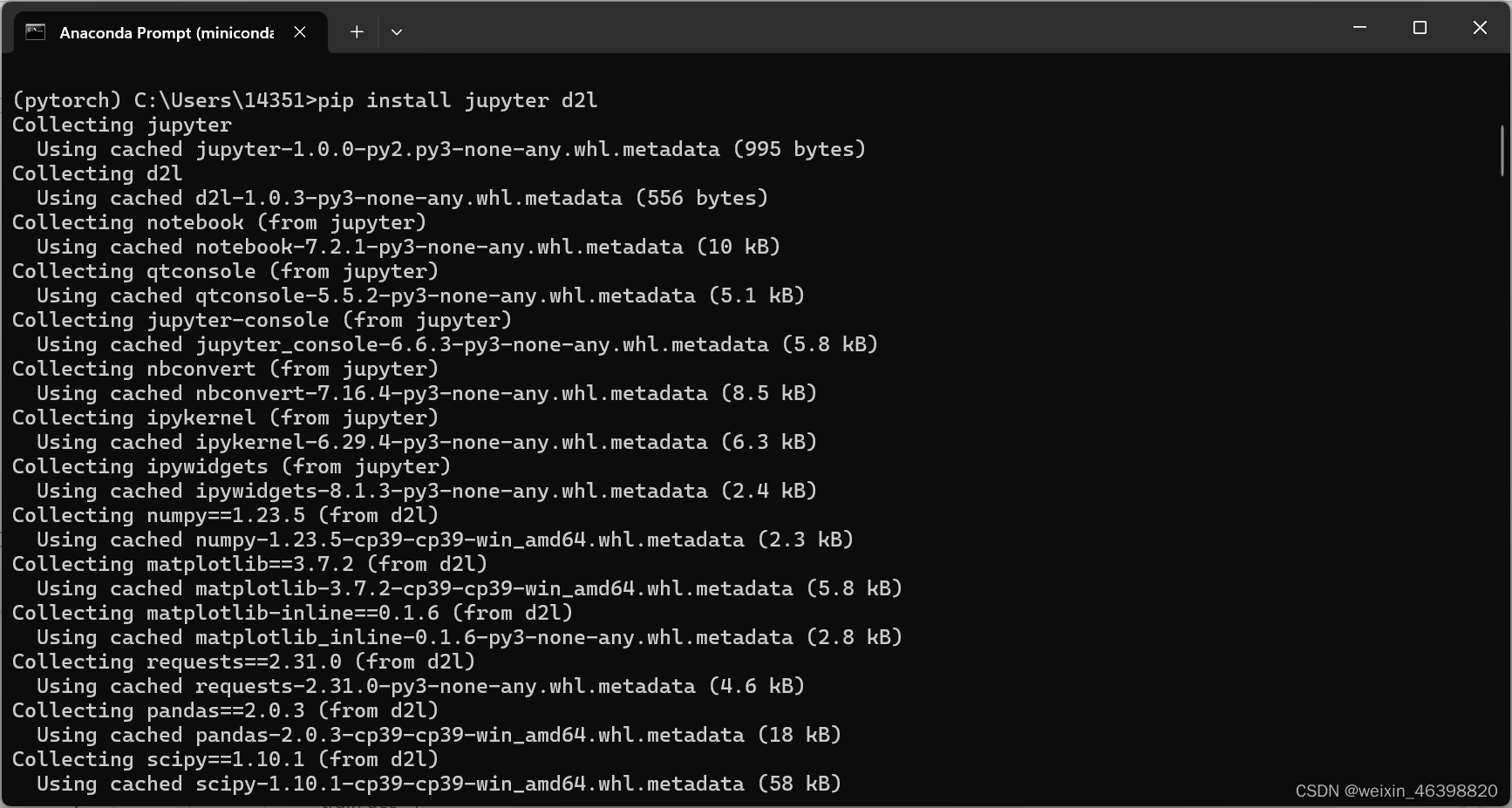
5 下载d2l运行测试

动手学深度学习

2.1 数据操作

N维数组是机器学习和神经网络的主要数据结构

创建数组需要形状（例如3*4的矩阵）、每个元素的数据类型（例如32位浮点数）、每个元素的值（例如全是0，或者随机数）。

访问元素：

张量表示一个由数值组成的数组，这个数组可能有多个维度。 具有一个轴的张量对应数学上的向量（vector）； 具有两个轴的张量对应数学上的矩阵（matrix）； 具有两个轴以上的张量没有特殊的数学名称。

数据操作实现：

运算符：

对于任意具有相同形状的张量， 常见的标准算术运算符（+、-、*、/和**）都可以被升级为按元素运算。

“按元素”方式可以应用更多的计算，包括像求幂这样的一元运算符。

我们也可以把多个张量连结（concatenate）在一起， 把它们端对端地叠起来形成一个更大的张量。

通过逻辑运算符构建二元张量。

对张量中的所有元素进行求和，会产生一个单元素张量。

在某些情况下，即使形状不同，我们仍然可以通过调用 广播机制（broadcasting mechanism）来执行按元素操作。 这种机制的工作方式如下：

1. 通过适当复制元素来扩展一个或两个数组，以便在转换之后，两个张量具有相同的形状；

2. 对生成的数组执行按元素操作。

运行一些操作可能会导致为新结果分配内存。 例如，如果我们用Y = X + Y，我们将取消引用Y指向的张量，而是指向新分配的内存处的张量。

 我们可以使用切片表示法将操作的结果分配给先前分配的数组，例如Y[:] = <expression>。

如果在后续计算中没有重复使用X， 我们也可以使用X[:] = X + Y或X += Y来减少操作的内存开销。

2.2 数据操作预处理

在Python中常用的数据分析工具中，我们通常使用pandas软件包。 像庞大的Python生态系统中的许多其他扩展包一样，pandas可以与张量兼容。 pandas可以预处理原始数据，并将原始数据转换为张量格式。

“NaN”项代表缺失值。 为了处理缺失的数据，典型的方法包括插值法和删除法， 其中插值法用一个替代值弥补缺失值，而删除法则直接忽略缺失值。这里使用插值法。

对于inputs中的类别值或离散值，我们将“NaN”视为一个类别。 由于“巷子类型”（“Alley”）列只接受两种类型的类别值“Pave”和“NaN”， pandas可以自动将此列转换为两列“Alley_Pave”和“Alley_nan”。 巷子类型为“Pave”的行会将“Alley_Pave”的值设置为1，“Alley_nan”的值设置为0。 缺少巷子类型的行会将“Alley_Pave”和“Alley_nan”分别设置为0和1。

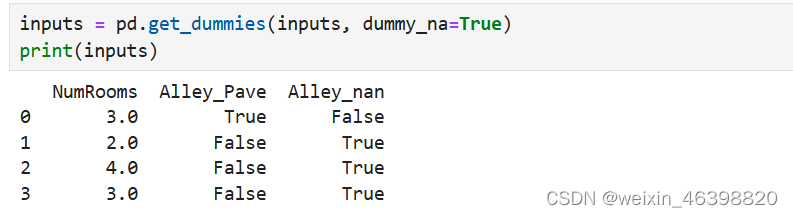
inputs和outputs中的所有条目都是数值类型，它们可以转换为张量格式。

2.3 线性代数

标量由只有一个元素的张量表示。

向量可以被视为标量值组成的列表。

矩阵，我们通常用粗体、大写字母来表示 （例如，𝑋、𝑌和𝑍）， 在代码中表示为具有两个轴的张量。

降维求和：我们可以对任意张量进行的一个有用的操作是计算其元素的和。 数学表示法使用∑符号表示求和。 为了表示长度为𝑑的向量中元素的总和，可以记为：

非降维求和：

点积：给定两个向量𝑥,𝑦∈𝑅𝑑， 它们的点积（dot product）𝑥⊤𝑦 （或〈𝑥,𝑦〉） 是相同位置的按元素乘积的和：

矩阵向量积𝐴𝑥是一个长度为𝑚的列向量， 其第𝑖个元素是点积𝑎𝑖⊤𝑥：

矩阵-矩阵乘法：

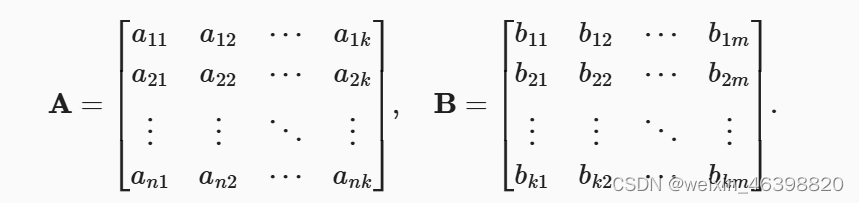
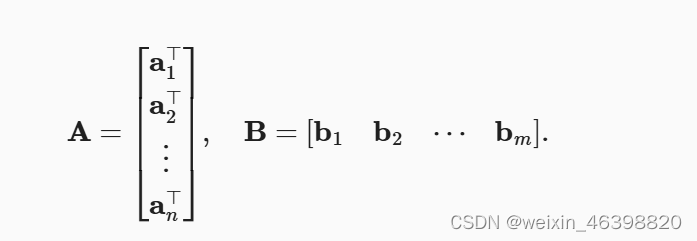
线性代数中最有用的一些运算符是范数（norm）。 非正式地说，向量的范数是表示一个向量有多大。 这里考虑的大小（size）概念不涉及维度，而是分量的大小。

欧几里得距离是一个𝐿2范数： 假设𝑛维向量𝑥中的元素是𝑥1,…,𝑥𝑛，其𝐿2范数是向量元素平方和的平方根：

深度学习中更经常地使用𝐿2范数的平方，也会经常遇到𝐿1范数，它表示为向量元素的绝对值之和：

2.4 微积分

微积分部分比较熟悉，因此不做记录。

2.5 自动微分

深度学习框架通过自动计算导数，即自动微分（automatic differentiation）来加快求导。 实际中，根据设计好的模型，系统会构建一个计算图（computational graph）， 来跟踪计算是哪些数据通过哪些操作组合起来产生输出。 自动微分使系统能够随后反向传播梯度。 这里，反向传播（backpropagate）意味着跟踪整个计算图，填充关于每个参数的偏导数。

计算图：

将代码分解成操作子；

将计算表示成一个无向图。

自动求导的两种模式：

自动求导实现：

对函数𝑦=2𝑥⊤𝑥关于列向量𝑥求导：

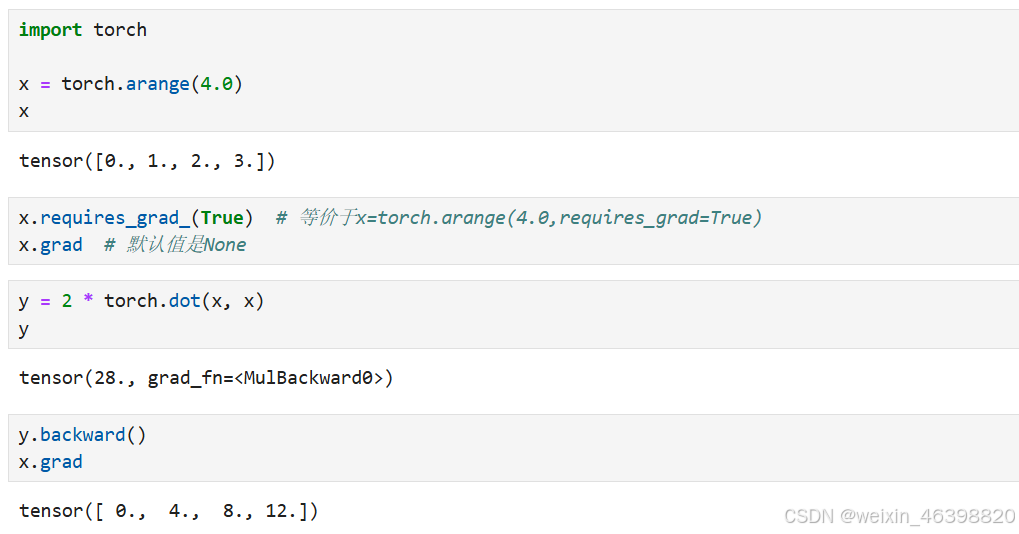
非标量变量的反向传播：

分离计算：

Python控制流的梯度计算：