Kruscal算法正确性证明

贪心算法：

贪心体现在两点

1.每次的选择一定是当前的最佳选择

2.只看眼前的利益，不把眼光放长远，不像回溯，贪心没有后悔药

所以贪心算法很容易陷入局部最优中

能用贪心算法解决的问题，应具有两个性质

1.最优子结构

官方解释：如果一个问题的最优解包含其子问题的最优解

一直理解不了这句话，举个例子

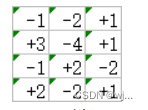
比如在这个图中，要从左下角到右上角，每次只能向上下左右四个方向移动，要求走过的路径和最大，可以验证得到这个结果的最佳路径中，从左下角的起点到右上角的终点路径中的每个点，其对应的路径和也是最大的

也就是对于从起点到终点的路所要求的最优，对于它的子问题，从起点到路径中的某点也是最优

这就是一个问题的最优解包含了子问题的最优解

2.贪心选择性

官方解释：所求问题的整体最优解可以通过一系列局部最优的选择来到达，即通过贪心选择来达到

贪心算法在图中的应用有最小生成树的Kruscal算法

这个怎么判断有没有贪心选择性有点难，记住常见的题型，比如活动排序、0-1背包、Kruscal算法等就行

Kruscal算法：

用不断加边的方式来得到最小生成树,Kruscal算法就是典型的贪心算法

1、每次选择最小的边

2、如果最小的边加入到已选的边以后不会产生回路，则在剩余的边中继续，否则去掉这条边

如何判断加入的边会产生回路呢？

初始每个顶点都赋予不同的标记，如果某条边被选中，就把其标记设为一样

这样在判断的时候，对于新加进来的边如果两个顶点标记不一样，说明它俩没关系，可以正常加进来，不会有回路

如果一样，则证明这两个点已经都在当前构造的树中，加入就会产生回路

如何证明Kruscal算法的正确性：

找了很多答案，才找到最容易理解的一种说法：

参考链接kruskal求得的生成树是最小生成树的证明_miss_minor的博客-CSDN博客

假如T是用Kruscal算法得到的生成树，U是这个图的最小生成树

如果能证明T的代价和U的代价一样大，那么就证明Kruscal得到的树就是最小生成树

我们用反证法

假如T和U不一样，那么肯定会有T中有，而U中没有的边

假如一共有K个这样的边，而e是这K个边中最小的一条边

我们从这条边e开始探讨

e不在U中，说明把e加到U中一定会形成环(因为U是最小生成树，定义)

我们取出形成的这个环中不在T中的最小的边f,（就是说f在U中，但不在T中，我把它取出来）

(其实环路中，除了e，其他边肯定不在T中，如果在T中，T就加不上e,因为会有回路)

现在分情况讨论e和f的值

如果说e和f代价是一样的，那么最后构造的T和U一定是代价一样的，也就是Kruscal算法得到的是最小生成树

如果说e<f,那么说明这个Kruscal得到的这个树要比最小生成树还要小，这是不可能的，所以这个之前的假设就不成立

如果e>f,那么T在选择的时候肯定不可能先选e啊，肯定捡小的先选

所以综上只有f=e这种情况可行

所以就证明了算法正确性

Kruscal算法实现：

图这部分算法，每次构造图的结构就很麻烦

对于最小生成树的两个算法以及最短路径算法都是用的邻接矩阵法（顺序存储结构）表示，而在拓扑排序和关键路径中用的是邻接表（即链表的形式）

顺序存储结构

关键核心是存储顶点的一维数组和存储边的二维数组，以及顶点数量vexnum和边的数量arcnum，这个顶点不需要重新构造顶点的结构体

邻接表存储结构

邻接表只需要存储顶点数组，但是顶点需要重新构造一个结构体，包括顶点数据以及该顶点链表中的一个指针，除了定义顶点外，由于存在链表，所以还需要定义链表中结点的结构体

平时Java用的较多，所以使用java来实现Kruscal算法

package Graph;

import java.util.Scanner;

public class Kruscal {
    //最小生成树 用邻接表存储
    //构造树时，需要有边的集合和点的集合
    public int arcnum;
    public int vexnum;
    edge[] edges;
    vertex[] vertices;
    //我们用的属于内部类,static+内部类相当于把它变成了外部类
     class edge{
        //三个内容，边的起点值，终点值，权值
        public int start;
        public int end;
        public int weight;

        public edge() {
        }

        public edge(int start, int end, int weight) {
            this.start = start;
            this.end = end;
            this.weight = weight;
        }
    }
    //每个顶点也用一个类来表示
     class vertex{
        //两个内容，边的值以及边所属集合
        //边所属集合是为了后期去判断加入该边是否会造成环
        int value;
        int sign;

        public vertex() {
        }

        public vertex(int value, int sign) {
            this.value = value;
            this.sign = sign;
        }
    }
//    构造无向网UDN
    public void createUDN()
    {
        Scanner in=new Scanner(System.in);
        this.vexnum=in.nextInt();
        this.vertices=new vertex[this.vexnum];
        this.arcnum=in.nextInt();
        this.edges=new edge[this.arcnum];
        for(int i=0;i<this.vexnum;i++)
        {
            vertex v=new vertex(in.nextInt(),i);
            vertices[i]=v;
        }
        for(int j=0;j<this.arcnum;j++)
        {
            edge e=new edge(in.nextInt(),in.nextInt(),in.nextInt());
            edges[j]=e;
        }
    }
    public void sort(edge[] edges)
    {
        //按照权值对这个数组进行排序，用最基本的冒泡
        for(int i=0;i<this.arcnum-1;i++)
        {
            for(int j=0;j+1<this.arcnum-i;j++)
            {
                if(edges[j].weight>edges[j+1].weight)
                {
                    //调换顺序,排序不仅要把权值对调，而是把整个对象对调
                    edge t=edges[j];
                    edges[j]=edges[j+1];
                    edges[j+1]=t;
                }
            }
        }
    }
    public edge[] kruscal()
    {
        //构造最小生成树,第一步对边进行排序
        //最小生成树的下标
        int index=0;
        sort(edges);
        edge[] minTree=new edge[vexnum-1];
        for(int i=0;i<this.arcnum;i++)
        {
            //选择最小的边，先判断这条边的两个顶点的标志一样不一样
            //注意存边时顶点值不是下标，而是真实值，我们要根据值找到它在顶点数组中的下标，从而看起始点的标志是不是一样
            int start=LocateVex(edges[i].start,vertices);
            int end=LocateVex(edges[i].end,vertices);
            int sign1=vertices[start].sign;
            int sign2=vertices[end].sign;
            //说明顶点存在，且加入这条边不会产生回路
            if(start!=-1&&end!=-1&&sign1!=sign2)
            {
                //将这条边加入到最小生成树中
                minTree[index++]=edges[i];
                //将与新加入的边的end顶点标记一样的全部改为和start一样的
                for(vertex v:vertices)
                {
                    if(v.sign==sign2)
                    {
                        v.sign=sign1;
                    }
                }
            }
            if(index==arcnum-1)
            {
                break;
            }
        }
        return minTree;

    }

    public int LocateVex(int start, vertex[] vertices) {
        for(int i=0;i<this.vexnum;i++)
        {
            if(vertices[i].value==start)
            {
                return i;
            }
        }
        return -1;
    }

    public void print(edge[] edges)
    {
        for(edge e:edges)
        {
            System.out.println(e.start+"->"+e.end+","+e.weight);
        }
    }


    public static void main(String[] args) {
        Kruscal k=new Kruscal();
        k.createUDN();
        edge[] minTree=k.kruscal();
        k.print(minTree);
    }

}

实现过程中需要注意，想要在main方法中新建内部类对象，必须把内部类改为static修饰

另外就是注意在根据对象的某个属性对对象排序时，不能只交换这个属性值，要把整个对象进行交换

如果在方法中传入数组，结果在方法中又重新定义了数组，这样无法实现修改数组的目的

比如说：

edge[] e=new edge[0];
test(e);

void test(edge[] e)
{
   e=new edge[5];
}

这样对e修改是不起作用的

输入：(原图)

 

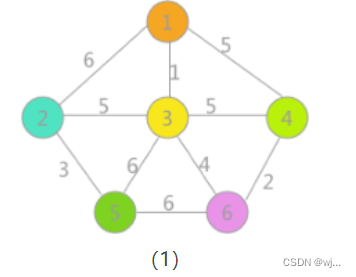
6 10
1
2
3
4
5
6
1 2 6
1 3 1
1 4 5
2 3 5
2 5 3
3 4 5
3 5 6
3 6 4
4 6 2
5 6 6

输出：

1->3,1
4->6,2
2->5,3
3->6,4
2->3,5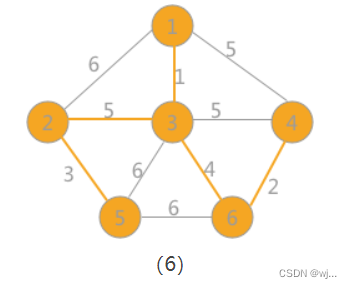

 

得到的最小生成树如上