<link rel="stylesheet" href="https://csdnimg.cn/release/blogv2/dist/mdeditor/css/editerView/kdoc_html_views-1a98987dfd.css">
<link rel="stylesheet" href="https://csdnimg.cn/release/blogv2/dist/mdeditor/css/editerView/ck_htmledit_views-25cebea3f9.css">
<div id="content_views" class="markdown_views prism-atom-one-dark">
<svg xmlns="http://www.w3.org/2000/svg" style="display: none;">
<path stroke-linecap="round" d="M5,0 0,2.5 5,5z" id="raphael-marker-block" style="-webkit-tap-highlight-color: rgba(0, 0, 0, 0);"></path>
</svg>
<h1><a name="t0"></a><a id="_0"></a>前言</h1>
传送门:
stable-diffusion-webui:Git
今年AIGC实在是太火了,让人大呼许多职业即将消失,比如既能帮忙写代码,又能写文章的ChatGPT。当然,还有AI绘画,输入一段文本就能生成相关的图像,stable diffusion便是其中一个重要分支。自己对其中的原理比较感兴趣,因此开启这个系列的文章来对stable diffusion的原理进行学习(主要是针对“文生图”[text to image])。
上述的stable-diffusion-webui是AUTOMATIC1111开发的一套UI操作界面,可以在自己的主机上搭建,无限生成图像(实测2080ti完全能够胜任),如果没有资源,可以白嫖Google Colab或者kaggle的GPU算力。
其中stable diffusion的基础模型可以hugging face下载,而C站可以下载各种风格的模型。stable diffusion有一个很大的优势就是基于C站中各式各样的模型,我们可以进行不同风格的AI绘画。
而这篇文章,首先对其中的一个组件进行学习:Autoencoder。
原理简介
Stable Diffusion is a latent text-to-image diffusion model。stable diffusion本质是一种latent diffusion models(LDMs),隐向量扩散模型。diffusion models (DMs)将图像的形成过程分解为去噪自动编码器(denoising autoencoders)的一系列操作,但这些都是直接在像素空间上进行的操作,因此对于昂贵的计算资源,特别是高像素的图像。而LDMs则是引入隐向量空间,能够生成超高像素的图像。
这里,我们先整体地来了解下stable diffusion的结构组成,后面再对每个组件进行拆开逐一理解。整体结构如下图[Stable Diffusion Architecture]:
- 文本编码器:人类输入的文本即prompt,经过CLIP模型中的Text Encoder,转化为语义向量(Token Embeddings);
- 图像生成器(Image information Creator):U-Net、采样器以及Autoencoder组成。由随机生成的纯噪声向量(即下图中的Noisey Image)开始,通过Autoencoder编码映射到低维的隐空间,文本语义向量作为控制条件进行指导,由U-Net和采样器不断迭代生成新的越具有丰富语义信息的隐向量,这就是扩散过程diffusion;
- 图像解码器(Image Decoder)- Autoencoder:迭代了一定次数之后,得到了包含丰富语义信息的隐向量(Processed Image Info Tensor),低维的隐向量经过Autoencoder解码到原始像素;
- 第2步就是LDMs和DMs的区别,LDMs是在latent space进行扩散,而DMs则是在pixel space,这也是性能提升的关键。

Autoencoder
[1] 论文:Taming Transformers for High-Resolution Image Synthesis
图片的隐空间表征从何而来:Autoencoder,既能够将图片从像素空间压缩到隐空间,让扩散过程在latent space中进行,又可以让图片从隐空间重建到像素空间(即图片重建),简化的过程如下图所示:
- 其中的encoder可以将一张图片从RGB空间即像素空间
x ∈ R H × W × 3 x\in \mathbb{R}^{H\times W \times 3} </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.5782em; vertical-align: -0.0391em;"></span><span class="mord mathnormal">x</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">∈</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.8413em;"></span><span class="mord"><span class="mord mathbb">R</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8413em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight" style="margin-right: 0.0813em;">H</span><span class="mbin mtight">×</span><span class="mord mathnormal mtight" style="margin-right: 0.1389em;">W</span><span class="mbin mtight">×</span><span class="mord mtight">3</span></span></span></span></span></span></span></span></span></span></span></span></span>,经过encoder编码到隐空间表征(latent representation)<span class="katex--inline"><span class="katex"><span class="katex-mathml"> z = ε ( x ) z= \varepsilon(x) </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal">ε</span><span class="mopen">(</span><span class="mord mathnormal">x</span><span class="mclose">)</span></span></span></span></span>;</li><li>decoder则是将隐空间表征重建到图片RGB <span class="katex--inline"><span class="katex"><span class="katex-mathml"> x ~ = D ( z ) = D ( ε ( x ) ) \tilde{x}=D(z)=D(\varepsilon(x)) </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6679em;"></span><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.6679em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord mathnormal">x</span></span><span class="" style="top: -3.35em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.2222em;"><span class="mord">~</span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.0278em;">D</span><span class="mopen">(</span><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.0278em;">D</span><span class="mopen">(</span><span class="mord mathnormal">ε</span><span class="mopen">(</span><span class="mord mathnormal">x</span><span class="mclose">))</span></span></span></span></span>;</li><li>其中,<span class="katex--inline"><span class="katex"><span class="katex-mathml"> z ∈ R h × w × c z\in \mathbb{R}^{h \times w \times c} </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.5782em; vertical-align: -0.0391em;"></span><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">∈</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.8491em;"></span><span class="mord"><span class="mord mathbb">R</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8491em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">h</span><span class="mbin mtight">×</span><span class="mord mathnormal mtight" style="margin-right: 0.0269em;">w</span><span class="mbin mtight">×</span><span class="mord mathnormal mtight">c</span></span></span></span></span></span></span></span></span></span></span></span></span>,重要的是,控制隐空间大小的是编码器的下采样因子(downsampling factors):<span class="katex--inline"><span class="katex"><span class="katex-mathml"> f = H / h = W / w , f = 2 m , m ∈ N f=H/h=W/w,f=2^m,m \in \mathbb{N} </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.8889em; vertical-align: -0.1944em;"></span><span class="mord mathnormal" style="margin-right: 0.1076em;">f</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.0813em;">H</span><span class="mord">/</span><span class="mord mathnormal">h</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.1389em;">W</span><span class="mord">/</span><span class="mord mathnormal" style="margin-right: 0.0269em;">w</span><span class="mord cjk_fallback">,</span><span class="mord mathnormal" style="margin-right: 0.1076em;">f</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.7224em; vertical-align: -0.0391em;"></span><span class="mord"><span class="mord">2</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.6644em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">m</span></span></span></span></span></span></span></span><span class="mord cjk_fallback">,</span><span class="mord mathnormal">m</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">∈</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.6889em;"></span><span class="mord mathbb">N</span></span></span></span></span></li></ul>

上述仅仅是从整体架构层面简单地描述了图片的隐空间与像素空间的转换与重建过程,但其实整个过程的细节还是比较复杂的,方法是出自VQGAN
[
1
]
^{[1]}
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.888em;"></span><span class="mord"><span class=""></span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">[</span><span class="mord mtight">1</span><span class="mclose mtight">]</span></span></span></span></span></span></span></span></span></span></span></span></span>,其结构如下图所示:</p>
- 论文认为高像素的图片合成需要模型能够理解图片的全局组成,使得局部和全局现实的生成能够保持一致。
- 因此,论文使用codebook来对图片的丰富视觉组成进行表征,而不是像素表征,codebook即是隐空间的表现形式。
- codebook可以大大减少的图片组成长度(相比像素),也使得能用transformer来高效地对图片内部的全局交互( global interrelations)进行建模。

Codebook
给定一张图片
x
∈
R
H
×
W
×
3
x\in \mathbb{R}^{H\times W \times 3}
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.5782em; vertical-align: -0.0391em;"></span><span class="mord mathnormal">x</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">∈</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.8413em;"></span><span class="mord"><span class="mord mathbb">R</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8413em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight" style="margin-right: 0.0813em;">H</span><span class="mbin mtight">×</span><span class="mord mathnormal mtight" style="margin-right: 0.1389em;">W</span><span class="mbin mtight">×</span><span class="mord mtight">3</span></span></span></span></span></span></span></span></span></span></span></span></span>,需要将x表征为离散空间的codebook集合 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
z
q
∈
R
h
×
w
×
n
z
z_q \in \mathbb{R}^{h\times w \times n_z}
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.8252em; vertical-align: -0.2861em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.1514em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right: 0.0359em;">q</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.2861em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">∈</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.8491em;"></span><span class="mord"><span class="mord mathbb">R</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8491em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">h</span><span class="mbin mtight">×</span><span class="mord mathnormal mtight" style="margin-right: 0.0269em;">w</span><span class="mbin mtight">×</span><span class="mord mtight"><span class="mord mathnormal mtight">n</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.1645em;"><span class="" style="top: -2.357em; margin-left: 0em; margin-right: 0.0714em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mathnormal mtight" style="margin-right: 0.044em;">z</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.143em;"><span class=""></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span>,其中<span class="katex--inline"><span class="katex"><span class="katex-mathml">
h
⋅
w
h \cdot w
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6944em;"></span><span class="mord mathnormal">h</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">⋅</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal" style="margin-right: 0.0269em;">w</span></span></span></span></span>可以认为是codebook中每个code的索引,而<span class="katex--inline"><span class="katex"><span class="katex-mathml">
n
z
n_z
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.5806em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathnormal">n</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.1514em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right: 0.044em;">z</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>是code的维度。学习这样的codebook表征需要以下几个组件:</p>
- 一个离散的codebook
Z = { z k } k = 1 K ∈ R n z Z=\{z_k\}^K_{k=1} \in \mathbb{R}^{n_z} </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6833em;"></span><span class="mord mathnormal" style="margin-right: 0.0715em;">Z</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1.1244em; vertical-align: -0.2831em;"></span><span class="mopen">{<!-- --></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3361em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right: 0.0315em;">k</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mclose"><span class="mclose">}</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.8413em;"><span class="" style="top: -2.4169em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight" style="margin-right: 0.0315em;">k</span><span class="mrel mtight">=</span><span class="mord mtight">1</span></span></span></span><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right: 0.0715em;">K</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.2831em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">∈</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.6889em;"></span><span class="mord"><span class="mord mathbb">R</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.6644em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span class="mord mathnormal mtight">n</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.1645em;"><span class="" style="top: -2.357em; margin-left: 0em; margin-right: 0.0714em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mathnormal mtight" style="margin-right: 0.044em;">z</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.143em;"><span class=""></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span>(可以当成embedding来理解,参数随机初始化,参与模型训练 ,但论文对这块没有清晰的描述,可以去看<a href="https://github.com/CompVis/taming-transformers/blob/master/taming/modules/vqvae/quantize.py#L31">源码</a>)</li><li><strong>CNN结构的encoder <em>E</em></strong>,可以将图片<span class="katex--inline"><span class="katex"><span class="katex-mathml"> x x </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal">x</span></span></span></span></span>编码为<span class="katex--inline"><span class="katex"><span class="katex-mathml"> z ^ ∈ R h × w × n z \hat{z} \in \mathbb{R}^{h\times w \times n_z} </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.7335em; vertical-align: -0.0391em;"></span><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.6944em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord mathnormal" style="margin-right: 0.044em;">z</span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.1944em;"><span class="mord">^</span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">∈</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.8491em;"></span><span class="mord"><span class="mord mathbb">R</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8491em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">h</span><span class="mbin mtight">×</span><span class="mord mathnormal mtight" style="margin-right: 0.0269em;">w</span><span class="mbin mtight">×</span><span class="mord mtight"><span class="mord mathnormal mtight">n</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.1645em;"><span class="" style="top: -2.357em; margin-left: 0em; margin-right: 0.0714em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mathnormal mtight" style="margin-right: 0.044em;">z</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.143em;"><span class=""></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></li><li><strong>CNN结构的decoder <em>G</em></strong>,能够将codebook <span class="katex--inline"><span class="katex"><span class="katex-mathml"> z q z_q </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.7167em; vertical-align: -0.2861em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.1514em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right: 0.0359em;">q</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.2861em;"><span class=""></span></span></span></span></span></span></span></span></span></span>重建为图像 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> x ^ \hat{x} </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6944em;"></span><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.6944em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord mathnormal">x</span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.2222em;"><span class="mord">^</span></span></span></span></span></span></span></span></span></span></span></li><li><strong>quantization</strong>操作,将<span class="katex--inline"><span class="katex"><span class="katex-mathml"> z ^ \hat{z} </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6944em;"></span><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.6944em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord mathnormal" style="margin-right: 0.044em;">z</span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.1944em;"><span class="mord">^</span></span></span></span></span></span></span></span></span></span></span>映射到<span class="katex--inline"><span class="katex"><span class="katex-mathml"> z q z_q </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.7167em; vertical-align: -0.2861em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.1514em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right: 0.0359em;">q</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.2861em;"><span class=""></span></span></span></span></span></span></span></span></span></span></li></ul>
具体的
z
q
z_q
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.7167em; vertical-align: -0.2861em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.1514em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right: 0.0359em;">q</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.2861em;"><span class=""></span></span></span></span></span></span></span></span></span></span>编码过程为:编码器<em>E</em>将x转化为<span class="katex--inline"><span class="katex"><span class="katex-mathml">
z
^
=
E
(
x
)
∈
R
h
×
w
×
n
z
\hat{z}=E(x) \in \mathbb{R}^{h\times w \times n_z}
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6944em;"></span><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.6944em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord mathnormal" style="margin-right: 0.044em;">z</span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.1944em;"><span class="mord">^</span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.0576em;">E</span><span class="mopen">(</span><span class="mord mathnormal">x</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">∈</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.8491em;"></span><span class="mord"><span class="mord mathbb">R</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8491em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">h</span><span class="mbin mtight">×</span><span class="mord mathnormal mtight" style="margin-right: 0.0269em;">w</span><span class="mbin mtight">×</span><span class="mord mtight"><span class="mord mathnormal mtight">n</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.1645em;"><span class="" style="top: -2.357em; margin-left: 0em; margin-right: 0.0714em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mathnormal mtight" style="margin-right: 0.044em;">z</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.143em;"><span class=""></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span>,然后通过element-wise quantization <span class="katex--inline"><span class="katex"><span class="katex-mathml">
q
(
⋅
)
q(\cdot)
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.0359em;">q</span><span class="mopen">(</span><span class="mord">⋅</span><span class="mclose">)</span></span></span></span></span>将每个离散的code <span class="katex--inline"><span class="katex"><span class="katex-mathml">
z
^
i
j
∈
R
n
z
\hat{z}_{ij} \in \mathbb{R}^{n_z}
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.9805em; vertical-align: -0.2861em;"></span><span class="mord"><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.6944em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord mathnormal" style="margin-right: 0.044em;">z</span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.1944em;"><span class="mord">^</span></span></span></span></span></span></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3117em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight" style="margin-right: 0.0572em;">ij</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.2861em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">∈</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.6889em;"></span><span class="mord"><span class="mord mathbb">R</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.6644em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span class="mord mathnormal mtight">n</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.1645em;"><span class="" style="top: -2.357em; margin-left: 0em; margin-right: 0.0714em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mathnormal mtight" style="margin-right: 0.044em;">z</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.143em;"><span class=""></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span>编码到距离最近的codebook entry <span class="katex--inline"><span class="katex"><span class="katex-mathml">
z
k
z_k
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.5806em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3361em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right: 0.0315em;">k</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>(这里产生的最邻近的<span class="katex--inline"><span class="katex"><span class="katex-mathml">
z
k
z_k
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.5806em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3361em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right: 0.0315em;">k</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>索引即为上图[VQGAN]的<span class="katex--inline"><span class="katex"><span class="katex-mathml">
s
i
s_i
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.5806em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathnormal">s</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3117em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>,后续会用到)<img src="https://img-blog.csdnimg.cn/img_convert/860e33216648e6a4d88368ca1eac22b6.png" alt=""><img src="https://img-blog.csdnimg.cn/img_convert/16b7214f5e89c51be20be3b5f6de8943.png" alt=""></p>
这部分的损失函数如下式
其中
L
r
e
c
=
∣
∣
x
−
x
^
∣
∣
2
L_{rec}=||x-\hat{x}||^2
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.8333em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathnormal">L</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.1514em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">rec</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">∣∣</span><span class="mord mathnormal">x</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1.0641em; vertical-align: -0.25em;"></span><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.6944em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord mathnormal">x</span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.2222em;"><span class="mord">^</span></span></span></span></span></span></span><span class="mord">∣</span><span class="mord"><span class="mord">∣</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8141em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></span></span>为<strong>重建loss</strong>,<span class="katex--inline"><span class="katex"><span class="katex-mathml">
s
g
[
⋅
]
sg[\cdot]
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal">s</span><span class="mord mathnormal" style="margin-right: 0.0359em;">g</span><span class="mopen">[</span><span class="mord">⋅</span><span class="mclose">]</span></span></span></span></span>为stop-gradient操作。由于<span class="katex--inline"><span class="katex"><span class="katex-mathml">
z
q
z_q
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.7167em; vertical-align: -0.2861em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.1514em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right: 0.0359em;">q</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.2861em;"><span class=""></span></span></span></span></span></span></span></span></span></span>的quantization操作是不可微分的,因此需要用到<a href="https://github.com/CompVis/taming-transformers/blob/master/taming/modules/vqvae/quantize.py#L81">梯度拷贝</a>(出自<a href="https://arxiv.org/pdf/1308.3432.pdf">straight-through gradient estimator</a>)</p>
Discriminator
论文:Image-to-Image Translation with Conditional Adversarial Networks
Git:https://github.com/phillipi/pix2pix
使用transformer来表征图片的隐性图像成分的分布,需要进一步逼近图片压缩的极限和学习更富含信息的codebook,因此,论文还训练一个patch-based的判别器D,让它能够区分真实和重建的图片:
真实图像和重建图像都会经过一个CNN结构的Discriminator,然后得到每个patch的预估概率,模型的训练目标就是让真实图像的预估概率尽量都为1,而重建图像的预估概率尽量都为0,简而言之,就是让Discriminator能够识别每个patch是来自真实图像还是重建图像,如下图红框部分:
上述这两部分是联合训练: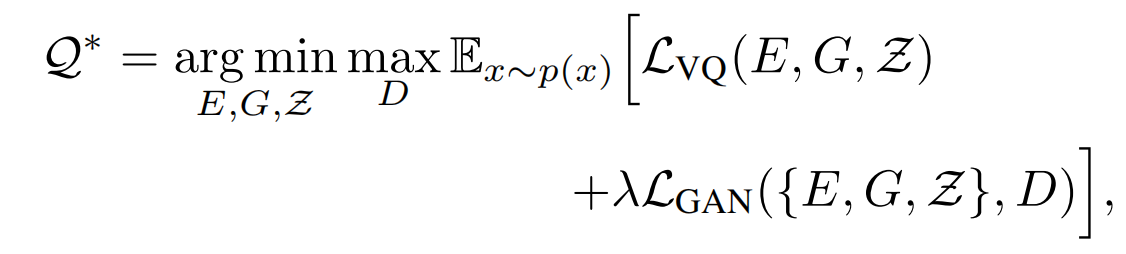

其中,
∇
G
L
[
⋅
]
\nabla_{G_L}[\cdot]
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.0003em; vertical-align: -0.2503em;"></span><span class="mord"><span class="mord">∇</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3283em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span class="mord mathnormal mtight">G</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3448em;"><span class="" style="top: -2.3567em; margin-left: 0em; margin-right: 0.0714em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mathnormal mtight">L</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.1433em;"><span class=""></span></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.2503em;"><span class=""></span></span></span></span></span></span><span class="mopen">[</span><span class="mord">⋅</span><span class="mclose">]</span></span></span></span></span>是decoder最后一层网络的梯度,而<span class="katex--inline"><span class="katex"><span class="katex-mathml">
δ
=
1
0
−
6
\delta=10^{-6}
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6944em;"></span><span class="mord mathnormal" style="margin-right: 0.0379em;">δ</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.8141em;"></span><span class="mord">1</span><span class="mord"><span class="mord">0</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8141em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">−</span><span class="mord mtight">6</span></span></span></span></span></span></span></span></span></span></span></span></span>。</p>
Transformers
Latent Transformers.
编码器E和解码器G训练完成之后,按照上述同样的操作,通过E和quantization操作,可以将图片
x
x
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal">x</span></span></span></span></span>表征到codebook <span class="katex--inline"><span class="katex"><span class="katex-mathml">
z
q
=
q
(
E
(
x
)
)
∈
R
h
×
w
×
n
z
z_q=q(E(x)) \in \mathbb{R}^{h \times w \times n_z}
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.7167em; vertical-align: -0.2861em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.1514em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right: 0.0359em;">q</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.2861em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.0359em;">q</span><span class="mopen">(</span><span class="mord mathnormal" style="margin-right: 0.0576em;">E</span><span class="mopen">(</span><span class="mord mathnormal">x</span><span class="mclose">))</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">∈</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.8491em;"></span><span class="mord"><span class="mord mathbb">R</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8491em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">h</span><span class="mbin mtight">×</span><span class="mord mathnormal mtight" style="margin-right: 0.0269em;">w</span><span class="mbin mtight">×</span><span class="mord mtight"><span class="mord mathnormal mtight">n</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.1645em;"><span class="" style="top: -2.357em; margin-left: 0em; margin-right: 0.0714em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mathnormal mtight" style="margin-right: 0.044em;">z</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.143em;"><span class=""></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span>,<span class="katex--inline"><span class="katex"><span class="katex-mathml">
h
⋅
w
h \cdot w
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6944em;"></span><span class="mord mathnormal">h</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">⋅</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal" style="margin-right: 0.0269em;">w</span></span></span></span></span>可以认为是codebook中每个code的索引<span class="katex--inline"><span class="katex"><span class="katex-mathml">
s
i
s_i
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.5806em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathnormal">s</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3117em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>,然后将二维的索引变为一维的,相当于一个code序列 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
s
∈
{
0
,
.
.
.
,
∣
Z
∣
−
1
}
h
×
w
s \in \{0,...,|Z|-1\}^{h \times w}
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.5782em; vertical-align: -0.0391em;"></span><span class="mord mathnormal">s</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">∈</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">{<!-- --></span><span class="mord">0</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="mord">...</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="mord">∣</span><span class="mord mathnormal" style="margin-right: 0.0715em;">Z</span><span class="mord">∣</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1.0991em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mclose"><span class="mclose">}</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8491em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">h</span><span class="mbin mtight">×</span><span class="mord mathnormal mtight" style="margin-right: 0.0269em;">w</span></span></span></span></span></span></span></span></span></span></span></span></span>:<img src="https://img-blog.csdnimg.cn/img_convert/0b1143e1c99c07391af0336518443edb.png" alt=""></p>
到这里,我们就可以按照NLP的自回归模型“预测下一个词”的思路来理解:给定code索引序列(上文)
s
<
i
s<i
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.5782em; vertical-align: -0.0391em;"></span><span class="mord mathnormal">s</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel"><</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.6595em;"></span><span class="mord mathnormal">i</span></span></span></span></span>,利用transformer来学习下一个code索引(下文)的概率分布 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
p
(
s
i
∣
s
<
i
)
p(s_i|s<i)
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal">p</span><span class="mopen">(</span><span class="mord"><span class="mord mathnormal">s</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3117em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mord">∣</span><span class="mord mathnormal">s</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel"><</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal">i</span><span class="mclose">)</span></span></span></span></span>,最大化完整表征序列的似然估计 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
p
(
s
)
=
∏
i
p
(
s
i
∣
s
<
i
)
p(s)=\prod_ip(s_i|s<i)
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal">p</span><span class="mopen">(</span><span class="mord mathnormal">s</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1.0497em; vertical-align: -0.2997em;"></span><span class="mop"><span class="mop op-symbol small-op" style="position: relative; top: 0em;">∏</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.162em;"><span class="" style="top: -2.4003em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.2997em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="mord mathnormal">p</span><span class="mopen">(</span><span class="mord"><span class="mord mathnormal">s</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3117em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mord">∣</span><span class="mord mathnormal">s</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel"><</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal">i</span><span class="mclose">)</span></span></span></span></span>:<img src="https://img-blog.csdnimg.cn/img_convert/bb0aad904eb9c42689b04e7ba090c0c8.png" alt=""></p>
Conditioned Synthesis.
在许多图片合成任务中,往往会加入额外的信息来控制图片的合成过程,这个额外信息称为
c
c
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal">c</span></span></span></span></span>,它可以是一个对图片的标签描述或者另外的图片。那么,学习的似然估计则变为:<img src="https://img-blog.csdnimg.cn/img_convert/90c1f360039ece3a7c1f26c58981e3be.png" alt=""></p>
机制理解
在最后,通过源码仓库里的两个实操案例notebook来理解Autoencoder这些组建的工作机制。
VQGAN可以将图片输入编码到低维的codebook空间(隐空间),然后再对codebook空间重建为图片的像素空间,如下图所示。更重要的是,这个过程的中间产物-隐空间,相较于像素空间,能够以很小的特征空间来表征图片,可以迁移到attention机制底座的模型训练的下流任务,比如本文的主题:Stable Diffusion。
def reconstruct_with_vqgan(x, model):
# could also use model(x) for reconstruction but use explicit encoding and decoding here
z, _, [_, _, indices] = model.encode(x)
print(f"VQGAN --- {model.__class__.__name__}: latent shape: {z.shape[2:]}")
xrec = model.decode(z)
return xrec
- 1
- 2
- 3
- 4
- 5
- 6

草图绘画.
这里主要是可以帮助理解VQGAN中Transformer的作用:
- 草图经过VQGAN的编码器得到codebook索引序列c-
s i s_i </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.5806em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathnormal">s</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3117em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>(c-仅是前缀,为了与成品图进行区分);</li><li>随机生成 成品图的codebook索引序列z-<span class="katex--inline"><span class="katex"><span class="katex-mathml"> s i s_i </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.5806em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathnormal">s</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3117em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>;</li><li>然后草图的索引序列c-<span class="katex--inline"><span class="katex"><span class="katex-mathml"> s i s_i </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.5806em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathnormal">s</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3117em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>作为控制条件,即上述提到Conditioned Synthesis章节中的<span class="katex--inline"><span class="katex"><span class="katex-mathml"> c c </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal">c</span></span></span></span></span>,拼接在z-<span class="katex--inline"><span class="katex"><span class="katex-mathml"> s i s_i </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.5806em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathnormal">s</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3117em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>的前面(z-<span class="katex--inline"><span class="katex"><span class="katex-mathml"> s i s_i </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.5806em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathnormal">s</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3117em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>每次截取一段),输入到Transformer,去预测z-<span class="katex--inline"><span class="katex"><span class="katex-mathml"> s i s_i </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.5806em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathnormal">s</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3117em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>的每一个位置,预测得到的索引逐步替代随机生成的索引序列;</li><li>最后,这个生成的索引序列再进入解码器<em>G</em>重建为图片(成品图)。</li></ul>


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








