数据结构从入门到入坟-二叉树

二叉树

二叉树的定义

二叉树（Binary Tree）是的一种特殊情况，因此定义与树一样。
在非空树中需要注意：除根结点外其余结点分为两个互不相交的子集，分别成为左子树（Lchild）、右子树（Rchild）
二叉树特点：二叉树结点的度小于等于2且它一定是有序树

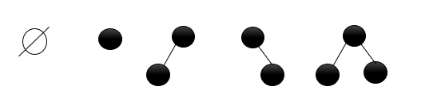二叉树的五种形式

二叉树的性质

• 性质1

  二叉树的第i层上最多有个$2^{i-1}$结点（i>=1）,最少有1个

  推导：“数学归纳法”

  • 当i=1时，第1层最多有$2^{1-1}=$1个结点

  • 当i=2时，第2层最多有$2^{2-1}=$2个结点

  • …

  • 依次类推，所以第i层最多有$2^{i-1}$个结点
    

• 性质2

  深度为K的二叉树最多有$2^k-1$个结点（i>=1），最少有K个

  证明：利用“性质1”可知第1层到第k层的最大结点数为：

  ​ $2^{1-1}+2^{2-1}+2^{3-1}+......+2^{k-1}=2^k-1$

  ​ 上式利用等比数列求和公式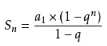求得
  当满足最多结点时二叉树成为满(或完美)二叉树

  按照从左往右的顺序插入结点的二叉树叫完全二叉树

• 性质3

  在一棵二叉树中，如果叶子结点的个数为$n_0$，度为2的结点个数为$n_2$，则$n_0=n_2+1$

  

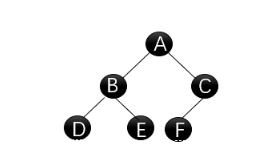
  证明：

  设：度为0的结点为$n_0$、度为1的结点为$n_1$、度为2的结点为$n_2$

  ​ 一方面，将度为0、1、2的结点加起来接受结点总数，那么结点总数**n=$n_0$+$n_1$+$n_2$ **（1）

  ​ 另一方面，0度的结点没有孩子，1、2度的结点有1、2个孩子，再加上根结点。

  ​ 我们就能推出n=$n_1$+$2n_2$ +1（2）

  ​ （1）与（2）联立可得$n_0=n_2+1$

• 性质4

  具有n个结点的完全二叉树的深度为$lo{g}_2^n+1$

  深度为n的完全二叉树它的n-1层以上所形成的树是满二叉树。那么，根据性质2可得深度为n-1的满二叉树结点数为$2^{n-1}-1$。所以，在第n层中最少有一个结点，那么n的最小值为$2^{n-1}$，又由性质2得最大值为$2^n-1$
  也就是 $2^{n-1}$$⩽$n$⩽$$2^n-1$ => $n-1\leqslant log_2^n \leqslant n $
  因此 $n\le log_2^n+1 \leqslant n+1 $（该证明不够直观，所以需要多练题增加印象）

  *例题:一棵完全二叉树上有1001个结点，其中叶子结点的个数是?
  解：n=$n_0+n_1+n_2$（下标是孩子结点个数，因此$n_0$是叶子结点）
  根据性质2可算出$n^9-1=511<1001<2^{1}0-1=1024$，也就说明该二叉树的最后一层有490（1001-511）个叶子结点；但是，如果为满二叉树那么根据性质1可得出最后一层为512个，现在少了22个，说明第九层还有叶子结点，那么这22个少了的结点对应了11个叶子结点，所以490+11=501

• 性质5
  对完全二叉树，若从上至下、从左至右编号,则编号为i的结点，其左孩子编号必为2i,其右孩子编号必为2i+1;其双亲的编号必为i/2.

---

​ *证明:含有n个结点的二叉链表中含有n+1个空链域
​ 因为n个节点有2n个指针
​ 又因为n个节点中有n-1条边（除了头结点没有边，其余节点都有 一个父节点，相当于都有1条边，共n-1条）
​ 剩下的空链域就是2n-(n-1)=n+1，即n+1个空指针

二叉树的存储

• 顺序存储

  

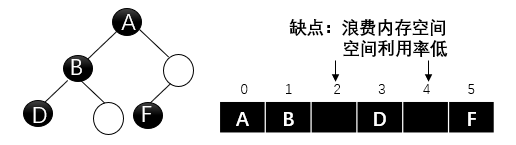
• 链表存储

  1. 二叉链表：左指针（lchild）、数据(data0)、右指针(rchild)

  2. 三叉链表：在二叉链表的基础上多一个双亲指针(parent)指向上一级

*二叉树的遍历

​ 以下遍历为二叉链表遍历

• 先序遍历：从访问根开始，再访问左子树然后访问右子树，当访问为空时返回。

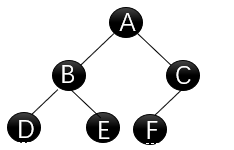  访问顺序：A-B-D-空-空-E-空-空-C-F-空-空-空遍历结果：ABDECF

• 中序遍历：左-根-右

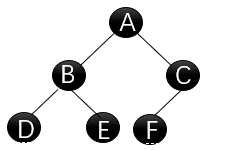  访问顺序：空-D-空-B-E-空-空-A-F-空-空-C-空

  遍历结果：DBEAFC

• 后序遍历：左-右-根

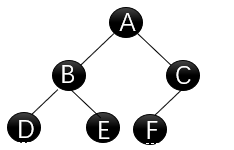  访问顺序：空-空-D-空-空-E-B-空-空-F-空-C-A

  遍历结果：DEBFCA

二叉树的创建与遍历

先序递归算法

二叉树结点的创建

typedef struct BiNode
{
	ElemType data;//数据域			  
	BiNode* lchild,* rchild;//左右子树结点
}*BiTree;//相当于struct BiNode *BiTree

先序递归创建二叉树

void createBiTree(BiTree& T)
{
	ElemType ch;
	cin >> ch;
	if (ch != '#')//当ch不是#时进入if语句
	{
		T = new BiNode;
		T->data = ch;
		createBiTree(T->lchild);
		createBiTree(T->rchild);
	}
	else T = NULL;//如果ch是#时则赋值T为空
}

先序、中序、后序遍历

//先序遍历
void preorderTraverse(BiTree T)
{
	if (T)
	{
		cout << T->data;
		preorderTraverse(T->lchild);
		preorderTraverse(T->rchild);
	}
}
//中序遍历
void inorderTraverse(BiTree T)
{
	if (T)
	{
		inorderTraverse(T->lchild);
		cout << T->data;
		inorderTraverse(T->rchild);
	}
}
//后序遍历
void postorderTraverse(BiTree T)
{
	if (T)
	{
		postorderTraverse(T->lchild);
		postorderTraverse(T->rchild); 
		cout << T->data;
	}
}

若有错误乞请斧正，感谢你的阅读。