分类型任务-CSDN博客

本文链接：https://blog.csdn.net/weixin_46886075/article/details/146112646

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

前言

现实中有很多问题并不是预测问题，所以在了解了线性回归的神经网络后，我们要开启分类领域，本章我们将会了解图片分类的工作流程，什么是卷积。

一、分类任务是什么？

回归与分类

在我们前面学习的分类任务中，给出一张散点图后，一般的目标的都是根据点的分布，找到预测线。而分类任务与预测任务不同，在分类任务中，我们面对散点图，需要的往往是根据不同点的特征不同，用分类线将这些点划分成各个种类。
在这里插入图片描述

如何做分类输出

如果我们将一段长度等长划分几段区间，归类时会归为距离最近的整数点，那么假设我们取得0.4。在分类时，0.4最近的整数点为0，这样我们就可以成功完成分类。
这种分类形式从结果来说，似乎没有问题，但让我们回归到原本步骤中。在判断分类时，我们会进行与各个整数点的距离比较，0.4与1的距离为0.6，与3的距离为2.6。这会对系统造成一个误会，这个点虽然属于0点，但判读其对另外两个1和3点的相似情况时，该点与1更加相像。举个例子，我虽然是人类，但在和猴子与鳄鱼比较相似情况下，明显与猴子更接近。可是，在我们分类任务中，很多情况下，大家的相似情况是等权重的，这便会产生误区了。
那么该如何接近这个问题呢？我们使用one-hot编码进行分类，One-Hot编码是一种将分类变量转换为数值形式的方法，常用于机器学习和数据处理。其核心思想是将每个类别转换为一个二进制向量，其中只有一个元素为1，其余为0。示例如下，
假设有一个颜色类别：红、绿、蓝。

红 → [1, 0, 0]

绿 → [0, 1, 0]

蓝 → [0, 0, 1]

图片分类

在图片分类任务中，我们会先将所有图片的尺寸大小进行统一为224224（默认习惯），再将图片输入模型，因为模型所需参数的数值是固定的。得到预测的概率分布（理解为一个n1的矩阵，矩阵内所有值的和1）后，概率分布中数值最大视为预测值，之后再与真实值求loss。
在这里插入图片描述

现在，我们又开始有了新的问题，就是如何将图片转换成输入的张量模式。大部分图片都是三原色为底，一张图片有三层通道，所以有一种方法是，将三个224224进行拉直，全部拉成一个大向量。但这种方法有个问题，全部拉直后会导致每次全连接过程中，产生大量的参数。一个简单的linear（3，4）就会产生16个参数，那么一个linear（3224*224，1000）产生的大量参数，很容易导致过拟合效果的产生。
那么我们应该如何进行输入呢？答：使用卷积神经网络。

二、卷积神经网络

什么是卷积神经网络

使用一个简单的引入方式（真实情况为黑盒），我们判断小图片图片是否属于大图片时，可以将两个图片都等尺寸的，拆成数量不等的正方形拼凑而成。然后按一定顺序进行对比，一层一层比较，最终找到结果。
下图中，我们假设红色小格为1，黑色小格为-1，卷积过程视为从左上角一层一层向下对比。对比方法为，将对应小格数值相乘，最后将所有对应小格数值相加。（-1）（-1）= 1，1 * 1 = 1，所以，当最终结果为9时，就是找到相同图片块的情况。
卷积神经网络中，卷是指一层一层滚动对比的过程，积是指两个小格对应值的乘积。其中，用于去对照（去卷）的图（小图）我们称为卷积核，被对比的（被卷的）的图（大图）我们称为特征图。我们卷积之后，生成的图像也成为特征图，因为新生成的图像，有时候还会被拿去，再次进行卷积。（想象一下多层全连接的过程）
卷积看似是图片进行对比，其本质是矩阵（图像的本质是矩阵）进行乘积运算。

通过卷积方法，我们很多时候判断一个图片的种类，往往不需要使用整个图片去进行卷积。比如，在下图中，我们就可以截取卷积核的特点，鸟喙、鸟爪，进行卷积匹配。

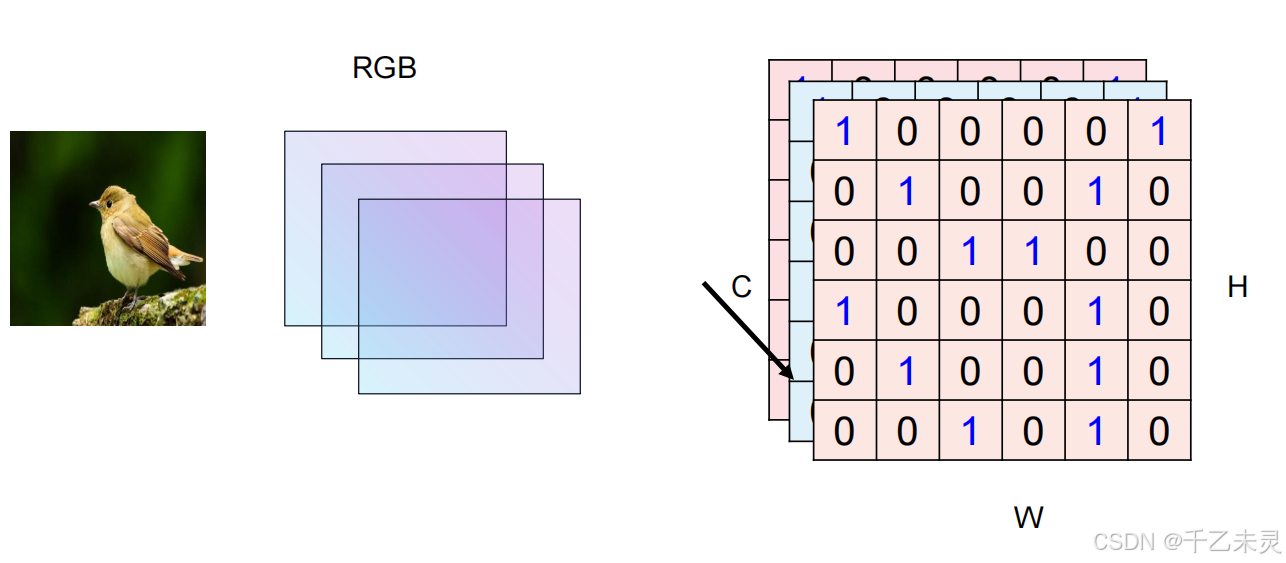
图片卷积时，并不是简单的单层卷积，往往是三层图片（RGB）进行卷积，CHW，C为通道表示厚度，H为高度，W为宽度。三层进行卷积，一个33*3的卷积核进行卷积，最终得到的结果为，27个积的和。卷积核的大小也被称为神经元的感受野，顾名思义是指卷积核能感受的视野面积。
在这里插入图片描述

零填充（zero padding）

我们发现每次卷积之后，特征图的大小都在减小，但在很多实际应用中，我们不需要也不希望特征图的大小发生变化，那么该如何解决这个问题呢？
在这里插入图片描述
通过零填充zero padding，在原特征图周围填充了一圈0后，生成的特征图便和之前一样。

更大的卷积核和更多的卷积核层数

更大的卷积核很简单，我们扩大卷积核的边长即可，如从33变为77。

我们现在再思考一下，当初使用全连接时，可以一层一层的连接下去，直到最终输出为1。那，如果我们卷积也想进行多次，有哪些需要注意的点呢？
上文说过，通过zero padding我们可以调整输出的特征图的高和宽，可是，图片有三个测量维度，他们还有具有通道特征。如下图，我们分别使用五个卷积核对特征图进行卷积，产生了五张新特征图。如果，我们想继续进行卷积，那么需要进行哪些操作呢？
答：将五张图叠起来，视作新的特征图，同时，我们的卷积核的通道数（即厚度）也要产生变化，需要和特征图进行对齐。即，卷积核的深度需要与特征图的深度进行对齐。
而一层卷积，就是指原始的特征图经过多个卷积核卷出来新的特征图，这个过程就是一层卷积。参数量的话，对于下图第一层卷积中，5333就是参数量（忽略bias情况下）。
下图，右下角灰色的特征图，就是堆叠后的高维特征图。
在这里插入图片描述

手算卷积神经网络

下面进行一些卷积题，方便进一步掌握卷积神经网络的原理。
在这里插入图片描述

特征图变小

我们学会了如何保持特征图不变之后，再次增加思考范围，如果想要将特征图变小，该怎么办？靠卷积一步一步减小吗？可行性差。所以，我们提出了以下方法。
subsampling，二次抽取，比如，我们在原特征图上每个一个像素点取一个，最终得出的图像完全不妨碍观察判断。实现这种降材，我们往往有两种方法，一种是扩大步长，另一种则是依靠池化Pooling。
在这里插入图片描述

扩大步长

卷积的步长并不一定为1。
在这里插入图片描述
卷积尺寸计算公式。

扩大步长应用较少，因为可能会丢失一定信息，同时还会引入一定计算量，增加复杂程度。

池化pooling

用多个格子来表示一个格子，对特征图进行放缩。
在这里插入图片描述

最大池化

顾名思义，根据所选范围中，最大的数来代表最终生成的值。
在这里插入图片描述

平均池化

顾名思义，根据所选范围中，平均值来代表最终生成的值。
在这里插入图片描述
实际应用中，最大池化应用更多，因为可以减少计算量。而且实战中，往往卷积和池化交替应用。

卷积到全连接

我们在经历了一系列卷积池化后，缩小了特征图的大小。最后就可以应用我们上文提过的方法。将图片（矩阵）进行拉直，转化为我们熟悉的全连接运算。
在这里插入图片描述

三、分类任务的Loss

概率化

可以利用softmax函数，将原本较大的值转化为概率函数。
在这里插入图片描述

交叉熵损失函数

在分类任务中，我们常常使用交叉熵损失函数来衡量预测值与真实值之间的差距，是优化模型参数的关键指标之一。交叉熵损失函数一般分为两类，一种是二分类，一种是多分类。
二分类，loss = $-[\hat{y}\log_{ }{ {y}'} +（1-\hat{y}）\log_{ }{ (1-{y}')}]$
当 $\hat{y}$ 趋近于0时，公式中前项 $\hat{y}\log_{ }{ {y}'}$ 为0，故只需要考虑后项 $（1-\hat{y}）\log_{ }{ (1-{y}')}$ ，此时 $1-\hat{y}$ 趋近于1， $log_{ }{ （1-{y}'）}$ 也趋近于0，整体是朝着loss值减小的方向发展。
当 $\hat{y}$ 趋近于1时，公式中后项 $（1-\hat{y}）$ 为0，故只需要考虑前项 $\hat{y}\log_{ }{ {y}'}$ ，此时 $\hat{y}$ 趋近于1， $log_{ }{ {y}'}$ 也趋近于0，整体依旧是朝着loss值减小的方向发展。
在这里插入图片描述
对于多分类，可以结合下图进行理解。

基本的分类神经网络工作流程

卷积+池化 -> 拉直+全连接 ->分类 + 概率化 ->交叉熵损失函数+梯度回传
在这里插入图片描述

四、数据集与模型

训练一个图片分类型的项目，往往需要大量的数据集进行提供，想要训练好则需要数百万张图片提供。下面介绍一些常见数据集。

MNIST数据集，提供一些简单从0到9的数字数据集。
Cifar10，是一个经典的小图片分类数据集，将图片分为10进行提供。
IMAGENET，大型图片数据集，有上百万张图片，分为1024。
COCO数据集，除了数据标签数据意外，还有一些文字描述。

在这里插入图片描述

经典神经网络模型

AlexNet

创新点：relu，dropout，池化，归一化
relu：方便计算，一定程度上防止梯度消失。
dropout：在传递过程中，随机选取一些抛弃不选。可以缓解过拟合
归一化：可以让模型关注数据的分布，而不受数据量纲的影响，还可以保持学习有效性，缓解梯度消失和梯度爆炸。
举两个归一化方法，Feature Normalization，Batch Norm
Feature Normalization，对同一行进行进行标准化。
在这里插入图片描述
Batch Norm，将一批数据进行归一化。

conv2d的全称为2D Convolution，即二维卷积。它是卷积神经网络（CNN）中的一种操作，专门用于处理二维数据（如图像）。
其中Pool（3，2）的意思是大小为3，步长为2的窗口进行池化。
注意该模型过程中，数据C，H，W的变化，了解数局变化情况可以方便我们深入理解该模型。
在这里插入图片描述

VggNet

在这里插入图片描述
我们用个例子，介绍一下用小卷积核代替大卷积核的情况，如下图，我们通过两个33小卷积核代替了一个55的大卷积核。参数量也从25减少到了18。

下面是AGG模型的基本流程，可以自行计算一下一个3224224通过该模型的过程中，数据的变化。
在这里插入图片描述

ResNet

在介绍ResNet模型之前，我们先介绍一下梯度消失和梯度爆炸。

梯度消失（Vanishing Gradient）

现象：
在反向传播过程中，梯度（即损失函数对参数的导数）逐层变小，导致浅层网络的参数几乎不更新，模型无法有效学习底层特征。

原因：

链式法则的连乘效应：梯度反向传播时需逐层计算偏导并相乘，若每层梯度绝对值小于1，深层梯度会指数级衰减。例如：若每层梯度为0.5，经过10层后梯度为 ${0.5}^{10}$ ≈ 0.00097。
激活函数的选择：使用饱和型激活函数（如Sigmoid、Tanh）时，导数在大部分区域接近0，进一步加剧梯度消失。Sigmoid导数范围：[0,0.25]，Tanh导数范围：[0,1]
权重初始化不当：若权重初始值过小，前向传播时激活值逐渐缩小，反向传播时梯度也随之减小。

影响：

浅层网络参数几乎不更新，模型仅依赖深层网络学习，性能严重受限。
常见于RNN、深层CNN等模型。

梯度爆炸（Exploding Gradient）

现象
反向传播时梯度逐层增大，导致参数更新幅度过大，模型无法收敛（损失剧烈震荡或变为NaN）。

原因

链式法则的连乘效应：若每层梯度绝对值大于1，深层梯度会指数级增长。例如：若每层梯度为2，经过10层后梯度为 ${2}^{10}$ =1024。
权重初始化不当：权重初始值过大，前向传播时激活值爆炸式增长，反向传播时梯度随之剧增。
学习率过高：过大的学习率会放大参数更新量，加剧梯度爆炸。

影响

参数更新失控，损失函数剧烈震荡或溢出（NaN）。
常见于深层前馈网络、RNN等模型。

解决方案
通用方法

方法	梯度消失	梯度爆炸
激活函数	使用ReLU、Leaky ReLU等非饱和函数	同左
权重初始化	He初始化（ReLU适用）	Xavier初始化（Tanh适用）
批量归一化（BN）	稳定激活值分布，缓解梯度问题	同左
残差连接	跳过连接传递梯度（如ResNet）	同左

在ResNet模型中，我们主要使用的是残差连接的方式解决，残差连接公式为Out = f(x) + x

模型设计

在这里插入图片描述
ResNet模型通过11卷积，并没有改变特征图大小，但可以通过缩减数量的方式去减少了参数量。

在残差连接过程中，会遇到一些情况Out = f(x) + x, 输出与输入层数大小维度不同怎么办？这个时候，可以将x通过11卷积，改变数量，再次加到out上。
在这里插入图片描述
RestNet模型结构