第一章：计算机组成与体系结构考点总结

历年考试情况分析

1、数据的表示

1.1 进制转换

1.1.1 R进制转十进制

按权展开法

写的详细一点就是：二进制 10100.01 = 1×2^4 + 0×2^3 + 1×2^2 + 0×2^1 + 0×2^0 + 0×2^(-1) + 1×2^(-2)，对于七进制604.01也是同样的道理。

1.1.2 十进制转R进制

短除法

对于十进制转R进制，采取的就是对十进制数除R取余，最后对余数取倒序即可。

---

如果将十进制数94转8进制，那么除8取余即可，其他情况均是如此。

1.1.3 二进制转八进制与十六进制

• 每三个二进制位对应一个八进制位
• 每四个二进制位对应一个十六进制位
  

二进制转八进制：对于二进制数10001110，从低位开始每三位对应一个八进制位，二进制的110对应八进制的6；二进制的001对应八进制的1；而此时只剩下两位10，那么在最前面补0（补满3位即可），也就是010，对应八进制的2，所以该二进制数10 001 110就对应八进制数216。

---

二进制转十六进制：对于二进制数10001110，从低位开始每四位对应一个十六进制位，二进制的1110对应十六进制的E(14)；二进制的1000对应十六进制的8；如果不满四位，与转八进制一样，在最前面补0（补满4位即可）。在十六进制中，A=10，B=11，C=12，D=13，E=14，F=15。

1.2 原码反码补码移码

1字节 = 8位

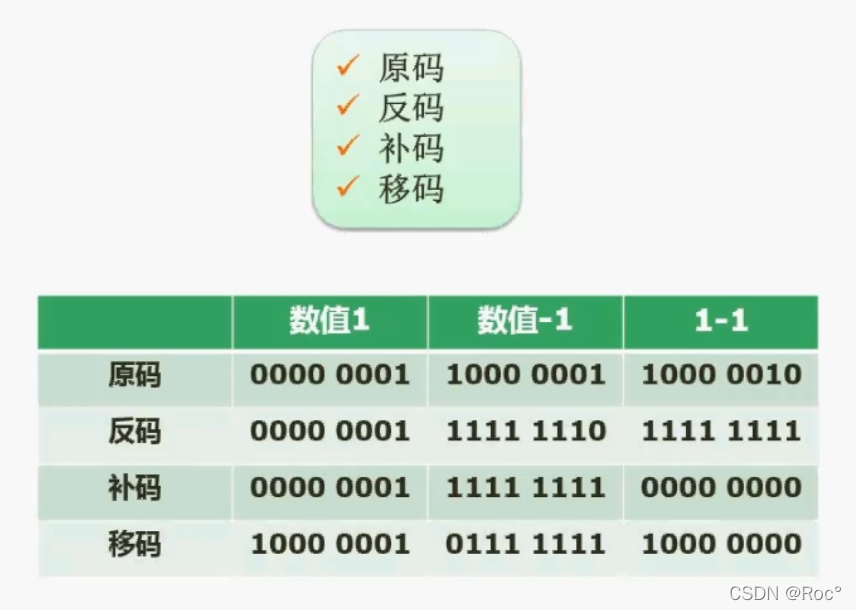
对于十进制数1，我们将其转为二进制为：1，如果用1个字节来存储它，我们会在它的左边补7个0（1个字节8位），也就是0000 0001，最高位是符号位（带符号的情况下），对于正数而言，符号位为0；对于负数，符号位为1。也就是说，对于正数1，它的原码就是0000 0001；对于负数1，它的原码就是1000 0001。

---

在上面的图表中，如果我们用原码进行1+（-1）的计算，会得到1000 0010这样的二进制数，此时的结果为-2。那么我们每个人都知道1+（-1）=0，所以原码表示的这种方式，是不能在机器中做直接的计算的。（用补码计算）

---

正数，它的原反补三码相同；
负数，它的反码为：符号位不变，其余位按位取反（1变0，0变1）；它的补码为：在原码的基础上，符号位不变，在剩下的位中，从低位开始找到第一个为1的那一位，从这个1开始的右边所有位都不变，左边所有位按位取反即可 （就是它的反码加1得到结果为补码）。

---

移码一般在特定的场合才会用到，比如浮点数运算中的阶码。而移码的求解方法，其实就是在补码的基础上，对于符号位进行取反即可。

• 机器字长为n时各种码制表示的带符号数的范围：

码制	定点整数	定点小数
原码	- (2^(n-1)-1) ~ + (2^(n-1)-1)	- (1-2^-(n-1)) ~ +(1-2^-(n-1))
反码	- (2^(n-1)-1) ~