

总结


注:这里的两个应该为同阶无穷大

注:这里的两个为同阶无穷小!总结为:同阶同敛散
拓展:瑕点
反常积分中的瑕点的含义: 如果函数f(x)在点a的一个邻域内无界,那么点a称为函数f(x)的瑕点(也称无界间断点)。无界函数的反常积分又称为瑕积分。 如果函数在点a的任一临域内都无界的意思是被积函数的第二类间断点,即在这点的被积函数不存在。 临域无界即这点的邻域是没有边界的,即不存在。判断反常函数的瑕点,不仅仅只是看分母为0的点,是所有使被积函数无意义的点。

反常积分的类型及于瑕点之间的关系: 1、无穷区间反常积分。 每个被积函数只能有一个无穷限,若上下限均为无穷限,则分区间积分。 2、无界函数反常积分。 即瑕积分,每个被积函数只能有一个瑕点,多个瑕点则分区间积分。 3、混合反常积分








 本文探讨了反常积分中的瑕点概念,指出瑕点是函数在某点无界的间断点,导致反常积分成为瑕积分。同阶无穷大与无穷小的关系在积分收敛性中起关键作用。反常积分主要分为三种类型:无穷区间反常积分、无界函数反常积分和混合反常积分。理解瑕点对于正确处理反常积分问题至关重要。
本文探讨了反常积分中的瑕点概念,指出瑕点是函数在某点无界的间断点,导致反常积分成为瑕积分。同阶无穷大与无穷小的关系在积分收敛性中起关键作用。反常积分主要分为三种类型:无穷区间反常积分、无界函数反常积分和混合反常积分。理解瑕点对于正确处理反常积分问题至关重要。




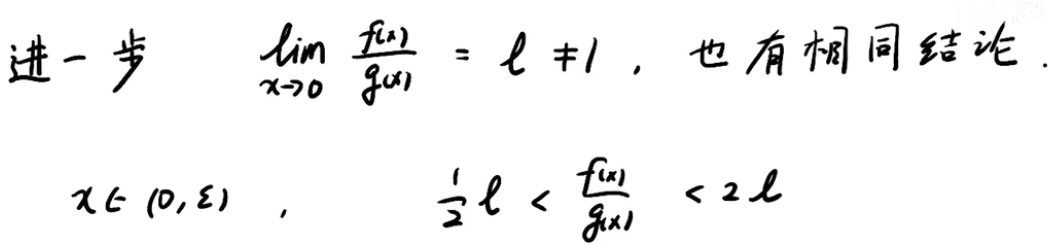


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










