高数 | 【多元函数微分学 计算篇】链式求导法、隐函数求导法、全微分形式不变性、多元函数求极值

一、多元函数微分法

1、链式求导法

 

 

 

 

 

 

 

 

---

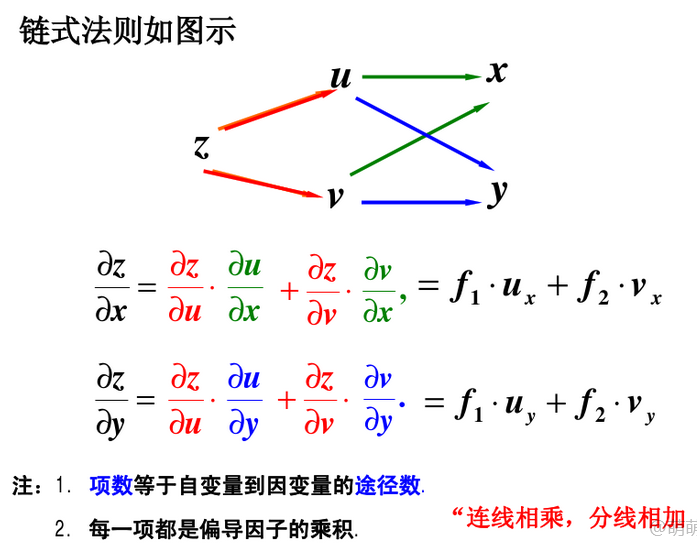
 2、全微分形式不变性

 全微分运算的四则运算性质

---

 3、隐函数微分法

3.1 一个方程的情形

•  经典例题

 

 

 

奇数个负1 偶数个正1

 3.2 方程组的情形

 

个人总结：（仅供参考）

1、方程组法（最简单，考试无脑用这个）
直接分析自由变量个数，每个方程两边同时直接对x求导，解方程组

2、链式求导法
第一种 分析变量之间关系：①根据题目中所给函数关系，画出树状关系图，注意叶子结点必须是自变量，且不能循环，然后按照复合函数求导来做
第二种 确定自由变量个数后，全部代成一个变量来做，使用公式法若有函数关系注意要将函数代入到最简 

3、全微分形式不变性

---

三、多元函数的极值与最值

1、无约束极值

 2、条件极值与拉格朗日乘数法

 3、最大最小值

---

四、常考题型与经典例题

1、连续、偏导数、全微分的概念及其之间的关系

可导但不连续的反例

 

 

 

2.复合函数的偏导数与全微分

 

 求导后的f1,f2,仍然是复合！

 

3.隐函数的偏导数与全微分

 4.求极值(无条件)

 

 解出原函数的两种方法：①偏积分  ②凑微分

 5.求连续函数f(x,y)在有界闭区域D上的最大最小值

 

 6.最大最小值应用题.

 

---

更新一道很多人都可能搞不清的题：

 

【答疑】

这里求 dz/dx 有些小机灵鬼想用隐函数存在定理即公式法。我们说了，公式法不就是把什么什么都看成常数吗，那y也看成常数，这题就显然不对了。

为什么呢？

你想用的隐函数存在定理 是 二元函数 z=f(x,y) 由 隐函数F(x,y,z)=0 所确定，这个时候才看成常数，而本题中，是 z=f(x) 是一元函数，就该用一元函数背景下的隐函数存在定理。

运算过程中y是x函数。