LeetCode 热题 100 - 回溯 - 单词搜索 - javascript

题目

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

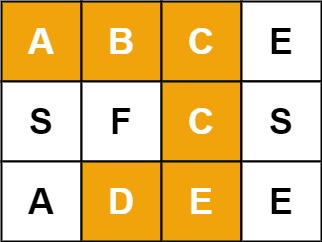
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2：

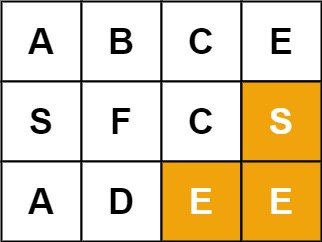
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出：true

示例 3：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出：false

解答

算法核心思想

这个算法采用了回溯法与深度优先搜索（DFS）相结合的策略：

1. 从每个单元格出发：尝试以矩阵中的每一个单元格作为单词的起点

2. 递归探索四个方向：对于每个匹配的字符，继续向上下左右四个方向探索

3. 标记已访问：避免重复使用同一个单元格

4. 回溯恢复状态：当一条路径不匹配时，回退并尝试其他路径

---

DFS 的详细执行流程：

1. 终止条件检查：

   • 如果当前字符匹配且是单词的最后一个字符，返回 true（找到完整匹配）

   • 如果当前字符不匹配，返回 false（这条路径无效）

2. 标记已访问：

   • 保存当前单元格的值到 temp

   • 将当前单元格标记为 undefined（表示已访问，防止重复使用）

3. 递归搜索四个方向：

   • 检查每个方向是否越界

   • 如果没有越界，则递归调用 dfs，index + 1 表示处理单词的下一个字符

   • 如果任一方向返回 true，则立即返回 true（找到匹配）

4. 回溯恢复：

   • 如果四个方向都没有找到匹配，恢复当前单元格的原始值

   • 返回 false 表示这条路径无效

var exist = function (board, word) {
    // 获取矩阵的行数和列数
    let row = board.length
    let col = board[0].length
    
    // 辅助函数：检查坐标是否越界
    const crossBorder = (x, y) => {
        return x < 0 || x >= row || y < 0 || y >= col
    }

    // 深度优先搜索函数
    const dfs = (i, j, index) => {
        // 基本情况1：找到完整匹配（当前字符匹配且是单词最后一个字符）
        if (board[i][j] === word[index] && index === word.length - 1) {
            return true
        }
        // 基本情况2：当前字符不匹配
        if (board[i][j] !== word[index]) {
            return false
        }

        // 保存当前字符值并标记为已访问（设置为undefined）
        let temp = board[i][j]
        board[i][j] = undefined
        
        // 向四个方向递归搜索：
        // 1. 检查是否越界
        // 2. 递归调用dfs，index+1表示处理下一个字符
        if (!crossBorder(i - 1, j) && dfs(i - 1, j, index + 1)) return true  // 上
        if (!crossBorder(i + 1, j) && dfs(i + 1, j, index + 1)) return true  // 下
        if (!crossBorder(i, j - 1) && dfs(i, j - 1, index + 1)) return true  // 左
        if (!crossBorder(i, j + 1) && dfs(i, j + 1, index + 1)) return true  // 右

        // 回溯：如果四个方向都没有找到匹配，恢复当前单元格的原始值
        board[i][j] = temp
        // 返回 false 表示这条路径无效
        return false
    }

    // 遍历矩阵中的每个单元格作为起点
    for (let i = 0; i < row; i++) {
        for (let j = 0; j < col; j++) {
            if (dfs(i, j, 0)) {  // 从单词的第一个字符开始搜索
                return true
            }
        }
    }
    return false
};