LeetCode 热题 100 - 二分查找 - 搜索二维矩阵 - javascript

题目

给你一个满足下述两条属性的 m x n 整数矩阵：

• 每行中的整数从左到右按非严格递增顺序排列。
• 每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

示例 1：

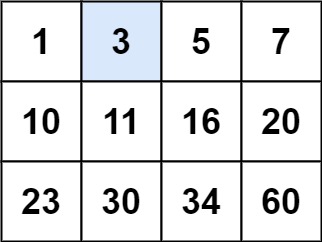
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

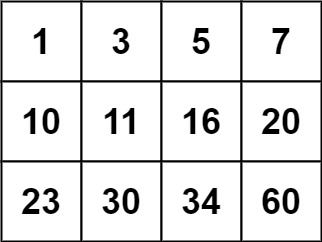
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

解答

算法思路详解：

1. 边界处理：

   • 首先检查矩阵是否为空或矩阵行是否为空，直接返回false

2. 二分查找确定行：

   • 通过比较每行最后一个元素与目标值，使用二分法缩小搜索范围

   • 如果目标值 > 当前行最后一个元素，搜索下方行

   • 如果目标值 < 当前行最后一个元素，搜索上方行

   • 如果正好等于，直接返回true

3. 行内线性搜索：

   • 确定目标行后，在该行内从左到右线性搜索目标值

   • 因为该行的最后一个元素≥target，且前一行的最后一个元素<target，所以目标值只可能在该行中

4. 边界条件处理：

   • 检查left是否超出矩阵范围（当目标值大于所有元素时），确保不会访问不存在的行

var searchMatrix = function (matrix, target) {
    // 边界检查：处理空矩阵或空行的情况
    if (!matrix.length || !matrix[0].length) return false;

    // 初始化二分查找的左右指针
    let left = 0;                   // 左指针初始化为第一行
    let right = matrix.length - 1;   // 右指针初始化为最后一行
    let len = matrix[0].length;      // 获取每行的长度（列数）

    // 第一步：二分查找确定目标值可能所在的行
    // 通过比较每行最后一个元素与目标值来确定搜索范围
    while (left <= right) {
        // 计算中间行
        let mid = Math.floor((left + right) / 2);
        
        // 比较中间行最后一个元素与目标值
        if (matrix[mid][len - 1] < target) {
            // 如果目标值大于该行最后一个元素，说明目标值可能在下方行
            left = mid + 1;
        } else if (matrix[mid][len - 1] === target) {
            // 如果正好等于该行最后一个元素，直接返回true
            return true;
        } else {
            // 如果目标值小于该行最后一个元素，说明目标值可能在该行或上方行
            right = mid - 1;
        }
    }
    // 循环结束后的left即为目标值所在行
    // 因为该行的最后一个元素≥target，且前一行的最后一个元素<target
    // 所以目标值只可能在该行中
    // 检查left是否有效（可能所有行都小于target，此时left会超出矩阵范围）
    if (left >= matrix.length) return false;
    
    // 第二步：在确定的行中线性搜索目标值
    for (let i = 0; i < len; i++) {
        if (matrix[left][i] === target) {
            return true;
        }
    }
    
    // 遍历完该行仍未找到目标值
    return false;
};