前言:
算法训练系列是做《代码随想录》一刷,个人的学习笔记和详细的解题思路,总共会有60篇博客来记录,计划用60天的时间刷完。
内容包括了面试常见的10类题目,分别是:数组,链表,哈希表,字符串,栈与队列,二叉树,回溯算法,贪心算法,动态规划,单调栈。
博客记录结构上分为 思路,代码实现,复杂度分析,思考和收获,四个方面。
目录
LeetCode300.最长递增子序列
链接:300. 最长递增子序列 - 力扣(LeetCode)
1. 思路
首先通过本题大家要明确什么是子序列,“子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序”。
本题也是代码随想录中子序列问题的第一题,如果没接触过这种题目的话,本题还是很难的,甚至想暴力去搜索也不知道怎么搜。 子序列问题是动态规划解决的经典问题,当前下标i的递增子序列长度,其实和i之前的下表j的子序列长度有关系,那又是什么样的关系呢。
接下来,我们依然用动规五部曲来分析详细一波:
1.1 dp[i]的定义
本题中,正确定义dp数组的含义十分重要。
dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度
为什么一定表示 “以nums[i]结尾的最长递增子序” ,因为我们在 做 递增比较的时候,如果比较 nums[j] 和 nums[i] 的大小,那么两个递增子序列一定分别以nums[j]为结尾 和 nums[i]为结尾, 要不然这个比较就没有意义了,不是尾部元素的比较那么 如何算递增呢。
1.2 递推公式
位置i的最长升序子序列 等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。
所以:if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
注意这里不是要dp[i] 与 dp[j] + 1进行比较,而是我们要取dp[j] + 1的最大值。
1.3 dp[i]的初始化
每一个i,对应的dp[i](即最长递增子序列)起始大小至少都是1,所以可以全部初始为1;
1.4 确定遍历顺序
dp[i] 是有0到i-1各个位置的最长递增子序列 推导而来,那么遍历i一定是从前向后遍历。
j其实就是遍历0到i-1,那么是从前到后,还是从后到前遍历都无所谓,只要吧 0 到 i-1 的元素都遍历了就行了。 所以默认习惯 从前向后遍历。
1.5 举例推导dp数组
输入:[0,1,0,3,2],dp数组的变化如下:
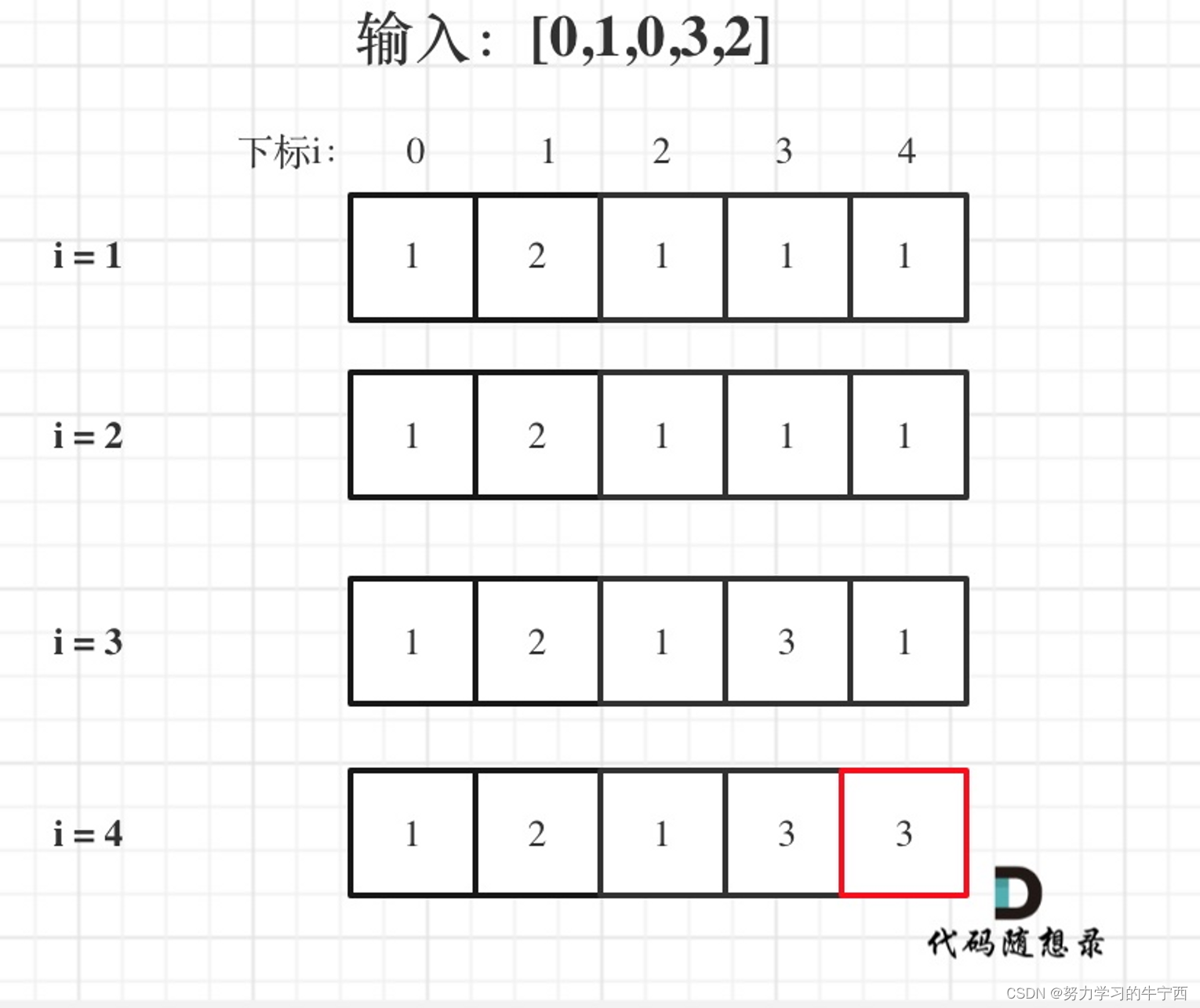
2. 代码实现
# 动态规划-子序列系列
# dp[i]: 以nums[i]为结尾的序列中,最长递增子序列的长度
class Solution(object):
def lengthOfLIS(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
dp = [1]*len(nums)
for i in range(1,len(nums)):
for j in range(0,i):
if nums[i] > nums[j]:
dp[i] = max(dp[i],dp[j]+1)
return max(dp)
C++代码实现
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
if (nums.size() <= 1) return nums.size();
vector<int> dp(nums.size(), 1);
int result = 0;
for (int i = 1; i < nums.size(); i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
}
if (dp[i] > result) result = dp[i]; // 取长的子序列
}
return result;
}
};
3. 复杂度分析
-
时间复杂度:O(n^2)
-
其中 n 为数组 nums 的长度;动态规划的状态数为 n,计算状态 dp[i]时,需要 O(n) 的时间遍历 dp[0…i−1] 的所有状态,所以总时间复杂度为 O(n^2);
-
空间复杂度:O(n)
其中 n 为数组 nums 的长度;需要额外使用长度为 n 的 dp数组。
4. 思考与收获
- 本题最关键的是要想到dp[i]由哪些状态可以推出来,并取最大值,那么很自然就能想到递推公式:dp[i] = max(dp[i], dp[j] + 1)
- 子序列问题是动态规划的一个重要系列,本题算是入门题目,好戏刚刚开始





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 600
600

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








