带你领略拼多多2020校招笔试题，这样的难度你可以搞定吗？

本文链接：https://blog.csdn.net/weixin_47340771/article/details/109459013

本文介绍了拼多多2020年校招笔试中的一道算法题，涉及动态规划和数据结构。题目要求找到最少操作次数将所有盒子的球清空，分析过程揭示了在大数范围下避免遍历的思考方式，以及通过递推公式解决问题的思路。适合面试准备和算法训练。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

大家好，本来今天想写一篇算法和数据结构的。但是看了一眼计划，发现基本上大部分基础的内容都已经讲过了。接下去就是一些竞赛相关的算法了，刚好最近是校招季，所以写一点笔试题的题解，也许对大家的招聘有点用。

这一次选了拼多多的校招笔试题其中的一题，在写文章的时候还看到了小马智行的。也就是那个楼教主创办的著名的pony.ai，但是我点进去看了一眼，发现大部分都是acm竞赛题的风格，难度对于普通学生而言有些高了。所以没有采纳，改选了拼多多的试题。

题意

给定一个整数N，代表N个盒子。第i个盒子当中有i个球。

我们可以选定一个N以内的自然数X，多多鸡会把所有盒中小球数量大于X的盒子减少X个球。现在想要用最少的步骤将所有盒子的球清空，请问最少需要多少次操作？

样例

第一行输入一个整数t，表示测试组数。

对于每一行都输入一个整数N（）

要求对于每组数据输出一个整数作为结果。

分析

我们仔细分析一下，会发现这题的难点有两个。第一个是这个N的范围太大了，对我们的复杂度限制得很高。第二点是盒子当中球的数量是动态的，在如此苛刻的复杂度要求下，我们很难掌握所有盒子的动态。

但如果你有足够多经验的话，会发现N的范围其实并不是限制而是提示。N的范围达到1e9，在这个量级下我们连的计算都是会超时的，也就是说所有需要遍历盒子的算法都可以放弃了，看似苛刻，其实会节省我们很多时间。如果N的范围给个1e6，那才是真的恶心。估计很多同学要被骗了，苦苦思考怎么样通过模拟的方法来计算。

既然范围是1e9，那么没地说，这题一定是通过一些巧妙的方法来计算的。但是究竟是什么巧妙的方法，我们干想是想不出来的，要想知道也不难，尝试着去做一下就可以找到门道了。

我们假设我们第一次选择了k，也就是序号大于等于k的盒子里球的数量都减少了k。那么减少之后的情况变成什么样了呢？我们列出来看看：。

有些同学看到这个可能会想第二个数字选什么，如果你这么想了，可能你做的题目还不够多，不够敏感。其实看到这个已经可以发现，当我们选择了k之后，数组被拆分成了两个部分，左边是0到k-1，右边是1到N-k，中间0是分割线。

这一点发现有什么用呢？其实很有用，我们首先来做一个假设，假设k-1 > N-k，也就是左边部分的元素比右边更多。那么不管我们接下来如何操作，其实只要我们的操作能够消除掉左边的部分，右边的自然也会跟着消除。同理，如果k-1 < N-k，也是一样的。所以我们通过选择了k之后，数组拆分成了两个部分，答案只和其中的一个部分有关，并且是和其中元素最多的部分有关。

那么根据这一点，我们可以直接写出表达式来表示N时的答案：

这个式子看起来很复杂不知道如何解，但其实也很简单，我们还有一个条件没有用上。就是f必然是一个递增函数，这个其实不需要严格证明，我们直观上就可以感受出来。既然f是递增函数，那么上面式子当中很多元素的大小关系就都明显了。

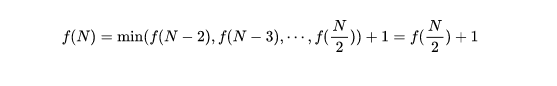
这样递推式就出来了，我们接下来要做的就是根据这个递推式写出它的通项。

我们把上面的式子全部累加在一起，右边带有f的项会被全部消掉，最终得到：。这个表达式有了，那么代码自然手到擒来。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <vector>
#include <cmath>
#include <cstdlib>
#include <string>
#include <map>
#include <set>
#include <algorithm>
#include "time.h"
#include <functional>
#define rep(i,a,b) for (int i=a;i<b;i++)
#define Rep(i,a,b) for (int i=a;i>=b;i--)
#define foreach(e,x) for (__typeof(x.begin()) e=x.begin();e!=x.end();e++)
#define mid ((l+r)>>1)
#define lson (k<<1)
#define rson (k<<1|1)
#define MEM(a,x) memset(a,x,sizeof a)
#define L ch[r][0]
#define R ch[r][1]
using namespace std;
const int N=1000050;
const long long Mod=1000000007;
int t, x;
int main() {
scanf("%d", &t);
rep(z, 0, t) {
scanf("%d", &x);
printf("%dn", int(log(x)/log(2)) + 1);
}
return 0;
}