捕食者-被捕食者方程组分析

捕食者-被捕食者方程组研究

《python数学实验与建模》中课后习题与代码解读2。

捕食者与被捕食者属于经典生态动力学问题，本次建模问题也是传统模型，并没有进行扩展。

一、问题描述

        假设封闭草原环境下，以兔子x(t)和狐狸y(t)的数量变化作为基本研究对象，x(0)=60,y(0)=60，并且假设只有这两种生物相互影响，没有其它外界影响。通过为期一定时间的观察，兔子与狐狸的基本观测值如下表所示：

        并且已知基本传统模型如下所示，要求根据观测值拟合求出a,b,c,d的值。

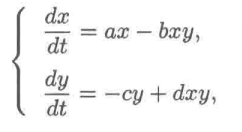
二、问题求解

        微分模型对于连续型数据具有意义，但是通过给出的表格数据，可以看出观测值属于离散量。所以可以将微分方程改为差分方程的形式。最终可将方程改写为Ax=b的形式（具体解析可查看司守奎老师的《python数学建模算法与应用》一书）。

求解过程python实现如下所示：

#利用线性最小二乘方法，估算整体的最小值
import numpy as np
t0 = np.