经典检测理论——极小极大值准则

1、基础前提——贝叶斯准则

• 贝叶斯准则的本质：使平均代价最小化，即$\underset{R_1}{\min }\overline{C}$
• 在已知先验分布的情况下，贝叶斯准则给出的平均错误代价为$$\overline{C}=\xi [c_{00}(1-P_F)+c_{10}{P}_F]+(1-\xi )[c_{01}{P}_M+c_{11}(1-P_M)]$$

注意：
1、$P_F$：虚报概率，且$P_F={\int }_{R1}{p}_0(x)dx$；
2、$P_M$：漏报概率，且$P_M={\int }_{R0}{p}_1(x)dx$；
3、$c_{ij}$：发生事件$H_j$，判决器判为$D_i$的代价因子，在二元数字通信系统中， i , j ∈ { 0 , 1 } i,j \in \lbrace{0,1\rbrace} i,j∈{0,1}

• 判决门限：${\lambda }_0=\frac{\xi (c_{10}-c_{00})}{(1-\xi )(c_{01}-c_{11})}$
• 判决准则：
  • 依据：似然比函数$\lambda (x)=\frac{p_1(x)}{p_0(x)}$
    ①当$\lambda (x)>{\lambda }_0$，接收端的判决器判为$D_1$，即判断发送端发送的是1（事件：$H_1$）；
    ②当$\lambda (x)<{\lambda }_0$，接收端的判决器判为$D_0$，即判断发送端发送的是0（事件：$H_0$）；

2、极小极大值准则

2.1 分析

1、贝叶斯准则是在已知先验分布的概率下得到的最小代价，即已知$p(H_1)=1-\xi ，p(H_0)=\xi$
2、如果先验分布未知，即$\xi$是未知量时，最小化代价是多少?（代价因子$c$已知）

2.2 先验概率未知下，最小代价的处理方法

• 1、先验概率未知，无法采用贝叶斯准则处理
• 2、如果假定先验概率并采用贝叶斯准则处理，则实际风险存在偏差，会导致风险增大，即代价会增加
• 3、两种策略：
  • 使最差情况下的风险极小化（极小极大风险）
  • 使偏差最小化（极小极大风险偏差）

2.3 以二元数字通信系统为例说明

例1：（二元数字通信系统）在时间间隔 T s内，要么发送一个幅度为d的脉冲，即有$s(t)=d$，代表“1”；要么在该时间间隔内不发送信号，即为$s(t)=0$，代表“0”。
在接收机处，接收信号由发送信号和信道噪声($n(t)$)组成，即有$r(t)=s(t)+n(t)$。依据对接收信号$r(t)$的一次抽样检测（单样本检测）来判断是否发送的信号是否为$s(t)=d$。

我们仍然以二元数字通信系统的例子为例，发送端发0或者1的概率密度函数如下图所示：

  
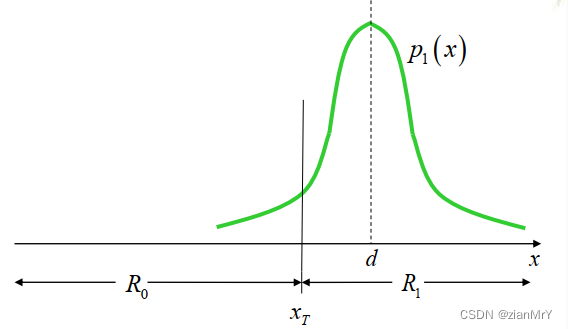
发送0                          发送1

根据贝叶斯准则计算，最小代价为：
$$\begin{gathered} {\overline{C}}_{min}=\xi [c_{00}{\int }_{-\infty }^{x_T}{p}_0(x)dx+c_{10}{\int }_{x_T}^{\infty }{p}_0(x)dx] \\ +(1-\xi )[c_{01}{\int }_{-\infty }^{x_T}{p}_1(x)dx+c_{11}{\int }_{x_T}^{\infty }{p}_1(x)dx] \end{gathered}$$
判决门限为：$${\lambda }_0=\lambda (x_T)=\frac{p_1(x)}{p_0(x)}=\frac{\xi (c_{10}-c_{00})}{(1-\xi )(c_{01}-c_{11})}$$

当我们将判决域划分为：$R_0$和$R_1$，且$R_0$和$R_1$为互备完斥集，则最小代价可以写成：$$\begin{gathered} {\overline{C}}_{min}=\xi [c_{00}{\int }_{R_0}{p}_0(x)dx+c_{10}{\int }_{R_1}{p}_0(x)dx] \\ +(1-\xi )[c_{01}{\int }_{R_0}{p}_1(x)dx+c_{11}{\int }_{R_1}{p}_1(x)dx] \end{gathered}$$

其中，虚报概率：$P_F={\int }_{R_1}{p}_0(x)dx=1-{\int }_{R_0}{p}_0(x)dx$;
漏报概率：$P_M={\int }_{R_0}{p}_1(x)dx=1-{\int }_{R_1}{p}_1(x)dx$
检测概率：$P_D={\int }_{R_1}{p}_1(x)dx$

• 由先验概率$\xi$，可以确定判决域$R_1$，从而可以确定判决门限${\lambda }_0$，也就是说，判决域和判决门限均由先验概率所确定；
• 在先验分布未知的情况下，将判决域视为关于先验概率$\xi$的函数，从而虚报概率、漏报概率也为关于$\xi$的函数，进而可以得到最小代价也是$\xi$的函数，表示如下：$$\begin{gathered} {\overline{C}}_{min}(\xi )=\xi [c_{00}(1-P_F(\xi ))+c_{10}{P}_F(\xi )] \\ +(1-\xi )[c_{01}{P}_M(\xi )+c_{11}(1-P_M(\xi ))] \end{gathered}$$

2.4 贝叶斯准则曲线

我们将最小代价描述为关于先验概率$\xi$的函数，并用如下曲线表示函数：$\overline{C}={\overline{C}}_{min}(\xi )$

• 问题1：为什么$\xi =0$或$\xi =1$时，代价为0？

  • $\xi =0$时，即发送端发送信号0的概率为0
    判决门限$\xi =\frac{p_1(x)}{p_0(x)}=\frac{\xi (c_{10}-c_{00})}{(1-\xi )(c_{01}-c_{11})}=0$
    接收端判决器全部判决为$D_1$，从而代价$\overline{C}=0$

  • $\xi =1$时，即发送端发送信号0的概率为1
    判决门限$\xi =\frac{p_1(x)}{p_0(x)}=\frac{\xi (c_{10}-c_{00})}{(1-\xi )(c_{01}-c_{11})}=\infty$
    接收端判决器全部判决为$D_0$，从而代价$\overline{C}=0$

    注意：判决正确视为没有代价，只有判决错误才会有代价

• 问题2：贝叶斯准则曲线为什么是凹函数（concave函数）？

  • 数学中，判断函数凹凸性的办法主要有以下两个：
    ①根据二阶导函数判断，二阶导数小于0，则为凹函数；
    ②几何法：在函数曲线上任取两点，两点之间连成的线段总在曲线的下方
  • 任取${\xi }_1\in (0,1)$，由${\xi }_1$可以确定判决域和判决门限，从而可以得到确定的虚报概率$P_F$和漏报概率$P_M$。
    实际情况下，$\xi$是系统真实的发送概率，且未知，而${\xi }_1$只是我们猜测或者说假定的一个先验概率值
    在这种猜测下，代价函数可以表示为：
    $$\begin{gathered} {\overline{C}}_{guess}(\xi ,{\xi }_1)=\xi [c_{00}(1-P_F({\xi }_1))+c_{10}{P}_F({\xi }_1)] \\ +(1-\xi )[c_{01}{P}_M({\xi }_1)+c_{11}(1-P_M({\xi }_1))] \end{gathered}$$
    令$C_{H_0}=c_{00}(1-P_F({\xi }_1))+c_{10}{P}_F({\xi }_1)$，
     $C_{H_1}=c_{01}{P}_M({\xi }_1)+c_{11}(1-P_M({\xi }_1))$
    则代价函数可以表示成：
    $${\overline{C}}_{guess}(\xi ,{\xi }_1)=\xi C_{H_0}+(1-\xi )C_{H_1}=C_{H_1}+\xi (C_{H_0}-C_{H_1})$$
    上述函数为过点$({\xi }_1,\overline{C}({\xi }_1))$ 所做出的一条直线，当$\xi \ne {\xi }_1$时，采用的为非贝叶斯准则的判决方式，所造成的代价会增大，所以直线${\overline{C}}_{guess}(\xi ,{\xi }_1)$会始终在贝叶斯准则曲线的上方，即曲线始终在直线的一侧。
    

    注意：
      如果我们采用的不是似然比检测器$\lambda (x)=\frac{p_1(x)}{p_0(x)}$，采用的是其它类型的检测器，猜测的先验概率下的代价函数${\overline{C}}_{guess}(\xi ,{\xi }_1)=\xi C_{H_0}+(1-\xi )C_{H_1}=C_{H_1}+\xi (C_{H_0}-C_{H_1})$在$\xi -\overline{C}$坐标轴上该如何画？
    解答：
      若采用的贝叶斯准则，则直线与贝叶斯准则曲线有交点；若采用的不是贝叶斯准则，则直线一定在贝叶斯准则曲线的上方。
    原因：
      一方面，似然比检测器是将接收到的实际变量一对一的映射为似然比；另一方面，贝叶斯准则是最小代价准则，其他准则所产生的代价不可能比贝叶斯准则下检测器所产生的代价小

2.5 猜测先验分布下，代价随$\xi$的变化趋势。

• 当猜测代价函数的斜率不为0时，具体如下图：
  
  当$\xi ={\xi }_1$时，该点的代价刚好对应贝叶斯准则曲线上的一点，在所有准则中代价最小；
  当$\xi :{\xi }_1\to 0$，$\overline{C}={\overline{C}}_{guess}(\xi ,{\xi }_1)$曲线与$\overline{C}={\overline{C}}_{min}(\xi )$曲线代价偏差逐渐增大，当$\xi =0$时，达到极大偏差；
  当$\xi :{\xi }_1\to 1$，$\overline{C}={\overline{C}}_{guess}(\xi ,{\xi }_1)$曲线与$\overline{C}={\overline{C}}_{min}(\xi )$曲线代价偏差逐渐增大，当$\xi =1$时，达到最大偏差；
• 当猜测函数斜率为0时，即无论$\xi$如何变换，猜测的先验分布下代价均不变，如下图所示：
  
  猜测先验分布下的代价函数：
  $${\overline{C}}_{guess}(\xi ,{\xi }_1)=\xi C_{H_0}+(1-\xi )C_{H_1}=C_{H_1}+\xi (C_{H_0}-C_{H_1})$$
  其中，$C_{H_0}=c_{00}(1-P_F({\xi }_1))+c_{10}{P}_F({\xi }_1)$，
     $C_{H_1}=c_{01}{P}_M({\xi }_1)+c_{11}(1-P_M({\xi }_1))$
  此时，$\xi =0$或$\xi =1$时所产生的代价相等，即：
  $$C_{H_0}=C_{H_1}$$
  根据上述式子，可以解出对应的${\xi }_1$，且满足${\xi }_1={\xi }_0$，此时代价函数简化为$${\overline{C}}_{guess}(\xi ,{\xi }_1)=C_{H_1}$$
  该情况对应的准则又叫等风险准则

注意：极小极大准则不是概率意义上的偏差最小，因此不是概率意义上的最优
$\Delta C(\xi ,{\xi }_1)=C_{min}(\xi )-C_{min}(\xi ,{\xi }_1)$
$\int p(\xi )\Delta C(\xi ,{\xi }_1)d\xi \to min$

3、极小极大风险准则面对的几种情况

注意：贝叶斯准则下的最小代价为：$$\begin{gathered} {\overline{C}}_{min}(\xi )=\xi [c_{00}(1-P_F(\xi ))+c_{10}{P}_F(\xi )] \\ +(1-\xi )[c_{01}{P}_M(\xi )+c_{11}(1-P_M(\xi ))] \end{gathered}$$
   当$\xi =0$，$P_M(\xi )=0\Rightarrow {\overline{C}}_{min}(\xi )=c_{11}$；
   当$\xi =1$，$P_F(\xi ))=0\Rightarrow {\overline{C}}_{min}(\xi )=c_{00}$

3.1 代价：$c_{00}=c_{11}=0$

$C_{H_0}=c_{00}(1-P_F({\xi }_1))+c_{10}{P}_F({\xi }_1)=c_{10}{P}_F({\xi }_1)$
$C_{H_1}=c_{01}{P}_M({\xi }_1)+c_{11}(1-P_M({\xi }_1))=c_{01}{P}_M({\xi }_1)$

3.2 代价：$c_{00}=c_{11}\ne 0$

3.3 代价：$c_{00}\ne c_{11}$

此时，当$\xi =0$与$\xi =1$时，偏差不相同。我们转动猜测代价函数所表示的直线，改变其斜率，使其斜率为：$$k=\frac{c_{00}-c_{11}}{1-0}$$
改变后的猜测代价函数直线与贝叶斯准则曲线的交点在${\xi }_1\ne {\xi }_0$处，且最大偏差比原来小，具体如下图所示：

• 如何确定该直线的斜率？
  猜测代价函数：
  $$\begin{gathered} {\overline{C}}_{guess}(\xi ,{\xi }_1)=\xi [c_{00}(1-P_F({\xi }_1))+c_{10}{P}_F({\xi }_1)] \\ +(1-\xi )[c_{01}{P}_M({\xi }_1)+c_{11}(1-P_M({\xi }_1))] \\ =c_{01}{P}_M({\xi }_1)+c_{11}(1-P_M({\xi }_1)) \\ +\xi [c_{00}(1-P_F({\xi }_1))+c_{10}{P}_F({\xi }_1)-[c_{01}{P}_M({\xi }_1)+c_{11}(1-P_M({\xi }_1))]] \end{gathered}$$
  从函数中可以得到，直线的斜率：
  $$\begin{gathered} k=c_{00}(1-P_F({\xi }_1))+c_{10}{P}_F({\xi }_1)-[c_{01}{P}_M({\xi }_1)+c_{11}(1-P_M({\xi }_1))] \\ =虚线斜率 \\ =\frac{c_{00}-c_{11}}{1-0} \end{gathered}$$
• 由上述有关斜率的关系式可以得到：
  等风险偏差策略：
  $$c_{00}(1-P_F({\xi }_1))+c_{10}{P}_F({\xi }_1)-c_{00}=c_{01}{P}_M({\xi }_1)+c_{11}(1-P_M({\xi }_1))-c_{11}$$

4、极小极大准则总结

准则	对应的策略
极小极大偏差	等风险偏差策略
极小极大代价	等风险策略

注意：当$c_{00}=c_{11}$时，极小极大代价$⟺$极小极大偏差，即二者等价

例1：二元数字通信系统（一次观测）

根据一次观测，用极小极大准则对下面两个假设做出判断：
$$\begin{gathered} H_1：r(t)=1+n(t) \\ {H}_0：r(t)=n(t) \end{gathered}$$
其中，$n(t)$为零均值，方差为${\sigma }^2$的高斯过程，且$c_{00}=c_{11}$，$c_{10}=c_{01}=1$。根据观测结果定出的判决门限是多少？给出的判决门限猜测的先验概率${\xi }_1$是多少？

• 答：根据极小极大准则，可以得出：$$c_{00}(1-P_F({\xi }_1))+c_{10}{P}_F({\xi }_1)-c_{00}=c_{01}{P}_M({\xi }_1)+c_{11}(1-P_M({\xi }_1))-c_{11}$$

  由于$c_{00}=c_{11}$，$c_{10}=c_{01}=1$，可以得到：$P_F({\xi }_1)=P_M({\xi }_1)$

  其中，$P_F=P(D_1|H_0)={\int }_{R_1}{p}_0(x)dx={\int }_{x_T}^{\infty }{p}_0(x)dx$
     $P_M=P(D_0|H_1)={\int }_{R_0}{p}_1(x)dx={\int }_{-\infty }^{x_T}{p}_1(x)dx$
  将$p_0(x)=\frac{1}{(2\pi {)}^{1/2}\sigma }{e}^{-\frac{x^2}{2{\sigma }^2}}$，$p_1(x)=\frac{1}{(2\pi {)}^{1/2}\sigma }{e}^{-\frac{（x-1{）}^2}{2{\sigma }^2}}$代入，根据正态分布的对称性，可以解得判决门限：$$x_T=\frac{1}{2}$$
  进一步，可以得到：$\lambda (x_T)=\frac{p_1(x_T)}{p_0(x_T)}=\frac{\xi (c_{10}-c_{00})}{(1-\xi )(c_{01}-c_{11})}=\frac{\xi }{1-\xi }=1$
  解得，对应的先验概率为：$\xi =\frac{1}{2}$

例2：在例1基础上，假定$c_{10}=3，c_{01}=6$

问题1：每个假设的先验概率为何值时达到最大的可能代价？
问题2：根据一次观测的判决域如何？

• 答：平均代价：$\overline{C}=c_{10}{P}_F+c_{01}{P}_M$
  根据等风险准则，得到：$c_{10}{P}_F=c_{01}{P}_M$，即：$P_F=2P_M$，可以得到关系式：

    ${\int }_{x_T}^{\infty }{p}_0(x)dx=2\ast {\int }_{-\infty }^{x_T}{p}_1(x)dx$

  $\Rightarrow$ ${\int }_{x_T}^{\infty }\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{x^2}{2{\sigma }^2}}dx=2\ast {\int }_{-\infty }^{x_T}\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{（x-1{）}^2}{2{\sigma }^2}}dx$

  $\Rightarrow$ ${\int }_{\frac{x_T}{\sigma }}^{\infty }\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x^2}{2}}dx=2\ast {\int }_{-\infty }^{\frac{x_T-1}{\sigma }}\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x^2}{2}}dx$
  当${\sigma }^2=1$，可以解得：$x_T=0.196937\approx 0.2$
  进一步可得到：$\lambda (x_T)=\frac{p_1(x_T)}{p_0(x_T)}=0.738553=\frac{\xi (c_{10}-c_{00})}{(1-\xi )(c_{01}-c_{11})}=\frac{\xi }{2(1-\xi )}$
  解得：$\xi \approx 0.5963$，即$p(H_0)=0.5963$