2025年4月14日：239，76, 53-CSDN博客

本文链接：https://blog.csdn.net/weixin_49442949/article/details/147232474

239：滑动窗口最大值

1.暴力求-双重循环-时间复杂度O(n*k)----超时

2.队列方法

队列中保存滑动过程中任意时刻的窗口最大值，里面的数据记录数组索引，索引对应的数组值从大到小排序。

遍历数组：

移除不在当前窗口内的元素索引。
// 队列不为空才能移出数据
// 队列的数组元素存储的索引值  <= i-k  说明窗口往右移动时，应该清除左边的不在窗口内的索引值（==也可以）
if (!deque.isEmpty() && deque.peekFirst() <= i - k) {
                deque.pollFirst();
            }
从队列尾部移除所有小于当前元素的元素索引，保证队列单调递减。
// 从队列尾部开始，移除所有小于当前元素的元素索引，保证队列递减，首个元素是窗口最大值的索引
//因此当前值最大时，队列数据会被全部删光
            while (!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {
                deque.pollLast();
            }
将当前元素的索引加入队列尾部。
 deque.offerLast(i);
当遍历到的元素个数达到窗口大小 k 及以上时，记录当前窗口的最大值到结果数组中

总结：队列存储索引值，是因为索引值才能更好地表明位置信息。先移除不属于当前窗口的索引值（第一步），然后对列表排序（第二步，第三部），记录结果（第四步）


class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums == null || nums.length == 0 || k <= 0) {
            return new int[0];
        }
        int n = nums.length;
        int[] result = new int[n - k + 1];
        // 双端队列，存储数组元素的索引
        Deque<Integer> deque = new LinkedList<>();
        

        for (int i = 0; i < n; i++) {
            // 如果队列头部的元素已经不在当前滑动窗口内，移除它
            if (!deque.isEmpty() && deque.peekFirst() == i - k) {
                deque.pollFirst();
            }
            // 从队列尾部开始，移除所有小于当前元素的元素索引
            while (!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {
                deque.pollLast();
            }
            // 将当前元素的索引加入队列尾部
            deque.offerLast(i);
            // 当滑动窗口的大小达到 k 时，记录当前窗口的最大值
            if (i >= k - 1) {
                result[i - k + 1] = nums[deque.peekFirst()];
            }
        }
        return result;
    }
}

76：放弃

class Solution {
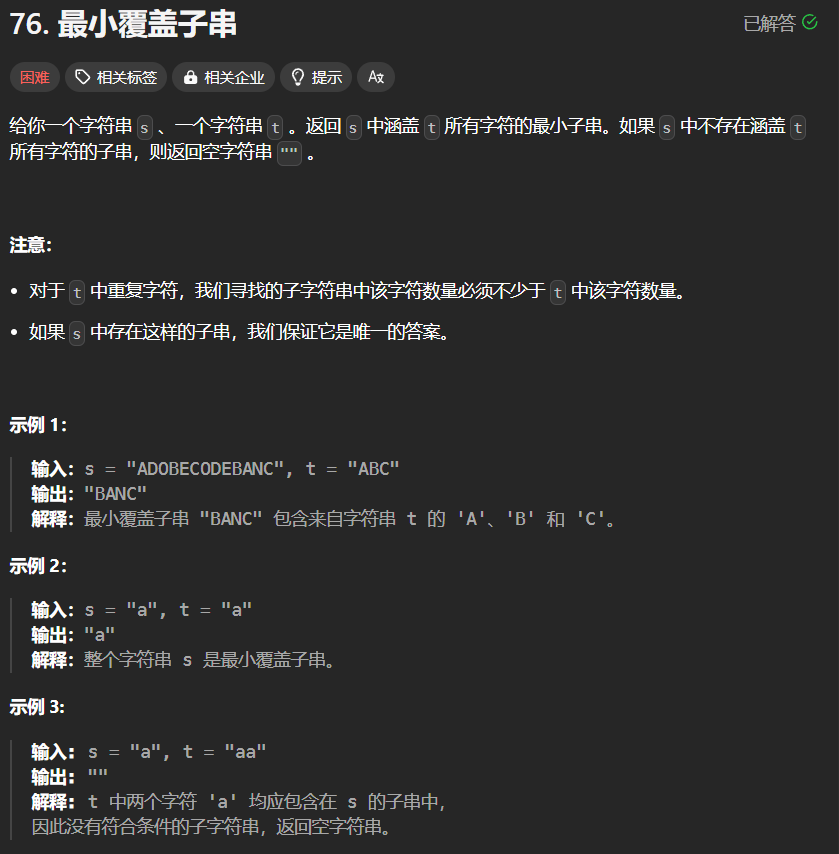
    public String minWindow(String s, String t) {
          if (s == null || s.length() == 0 || t == null || t.length() == 0) {
            return "";
        }
        // 统计 t 中每个字符的出现次数
        Map<Character, Integer> target = new HashMap<>();
        for (char c : t.toCharArray()) {
            target.put(c, target.getOrDefault(c, 0) + 1);
        }

        int left = 0, right = 0;
        int minLen = Integer.MAX_VALUE;
        int start = 0;
        int required = target.size();
        int formed = 0;
        Map<Character, Integer> window = new HashMap<>();

        while (right < s.length()) {
            char c = s.charAt(right);
            window.put(c, window.getOrDefault(c, 0) + 1);

            if (target.containsKey(c) && window.get(c).intValue() == target.get(c).intValue()) {
                formed++;
            }

            while (left <= right && formed == required) {
                c = s.charAt(left);

                if (right - left + 1 < minLen) {
                    minLen = right - left + 1;
                    start = left;
                }

                window.put(c, window.get(c) - 1);
                if (target.containsKey(c) && window.get(c).intValue() < target.get(c).intValue()) {
                    formed--;
                }
                left++;
            }
            right++;
        }
        return minLen == Integer.MAX_VALUE ? "" : s.substring(start, start + minLen);
    }
}

53. 最大子数和

方法一：使用之前的前缀和方法 -----但有7个测试用例超时

// 前缀和
class Solution {
    public int maxSubArray(int[] nums) {
    int max = nums[0];
     int[] presum = new int[nums.length+1];
     presum[0]=0;

//计算前缀和
     for(int i=0;i<nums.length; i++){
        presum[i+1]=presum[i]+nums[i]; 
     }  

     for(int i=0;i<nums.length; i++){  //i<nums.length,防止内循环越界，presum[nums.length]-presum[nums.length-1]就代表单独最后一个元素
        for(int j=i+1;j<nums.length+1; j++){
        int temp = presum[j]-presum[i];
        max = Math.max(temp,max);
     }
     }  
     return max;
    }
}

方法2：动态规划

// dp
class Solution {
    public int maxSubArray(int[] nums) {

    // 在动态规划中，dp 数组用于保存 子问题 的解。这里 dp[i] 表示以 nums[i] 结尾的连续子数组的最大和。
     int[] dp = new int[nums.length];
     dp[0] = nums[0];
     int  res = dp[0];

    //  从数组的第二个元素（索引为 1）开始遍历到数组的最后一个元素。这个循环的目的是依次计算以每个元素结尾的连续子数组的最大和。
     for(int i=1;i<nums.length; i++){
        dp[i] = Math.max(dp[i-1]+nums[i],nums[i]);  // 状态转移公式
        if(dp[i]>res) res = dp[i];
     }  
     return res;
    }
}

//12行代码：dp的核心--状态转移公式
// 对于 dp[i]，有两种选择：
// 一种是将当前元素 nums[i] 加入到 以nums[i - 1] 结尾的连续子数组中，此时和为 dp[i - 1] + nums[i]。
// 另一种是从当前元素 nums[i] 开始一个新的连续子数组，此时和为 nums[i]。
// 使用 Math.max 函数取这两种情况的最大值作为 dp[i] 的值，即 dp[i] 是以 nums[i] 结尾的连续子数组的最大和。