零基础入门转录组数据分析——列线图模型（诊断）

零基础入门转录组数据分析——列线图模型（诊断）

---

---

• 目录部分跳转链接： 零基础入门生信数据分析——导读

注：可根据自己的需求从总体目录中跳转到所需的分析点

---

1. 列线图模型的基础知识

1.1 什么是列线图？
列线图模型（Nomogram模型），又称诺莫图或诺模图，是一种基于多因素回归分析，将多个预测指标整合后，然后采用带有刻度的线段，按照一定的比例绘制在同一平面上，从而用以表达预测模型中各个变量之间的相互关系

1.2 列线图的基本原理是什么？
通过构建多因素回归模型（常用的回归模型，例如Cox回归、Logistic回归等），根据模型中各个影响因素对结局变量的贡献程度（回归系数的大小），给每个影响因素的取值水平进行赋分，然后再将各个评分相加得到总评分，最后通过总评分与结局事件发生概率之间的函数转换关系，从而计算出该个体结局事件发生的概率。（注：在预后的列线图模型里个体结局事件就是生存/死亡）

1.3 列线图的特点是什么？

• 直观性： 列线图通过图形化的方式展示预测模型中各变量的关系，使得非专业人士也能直观理解预测结果。
• 综合性： 能够综合考虑多个预测指标，提高预测的准确性。

1.4 构建列线图的注意事项

• 模型验证： 在构建列线图模型后，必须进行充分的模型验证，以确保预测结果的准确性和可靠性。
• 变量选择： 应基于科学研究和统计分析结果，合理选择对预测目标有显著影响的变量，通常是在前面经过层层筛选之后，将那些相对来说重要的变量用于构建列线图。

综上所述： 列线图就是将一些重要的变量用数值型刻度线段来表示，从而预测某种结局（例如：疾病）发生的概率。

---

配套资源领取链接：资源

注意：配套资源包含输入数据 + R脚本 + 输出结果

R脚本已经测试过可一键运行，搭配教程使用可复现结果，学习效果更佳

---

2. 列线图模型（诊断）（Rstudio）——代码实操

本项目以TCGA——肺腺癌为例展开分析
物种：人类（Homo sapiens）
R版本：4.2.2
R包：tidyverse, rms, pROC

废话不多说，代码如下：

2. 1 数据处理

设置工作空间：

rm(list = ls()) # 删除工作空间中所有的对象
setwd('/XX/XX/XX') # 设置工作路径
if(!dir.exists('./21_Nomogram_model_diagnosis')){
  dir.create('./21_Nomogram_model_diagnosis')
} 
setwd('./21_Nomogram_model_diagnosis/') 

加载包：

library(tidyverse)
library(rms) 
library(pROC)

导入要分析的表达矩阵TrainRawData，并对TrainRawData的列名进行处理（这是因为在读入的时候系统会默认把样本id中的“-”替换成“.”，所以要给替换回去）

注：关于TrainRawData的获取和处理见之前的章节：

零基础入门转录组下游分析——数据处理（TCGA数据库）

零基础入门转录组下游分析——数据处理（GEO数据库——芯片数据）

零基础入门转录组下游分析——数据处理（GEO数据库——高通量测序数据）

零基础入门转录组下游分析——数据处理（自测序数据）

TrainRawData <- read.csv("./data_fpkm.csv", row.names = 1, check.names = F)  # 行名为全部基因名，每列为样本名
colnames(TrainRawData) <- gsub('.', '-', colnames(TrainRawData), fixed = T)

TrainRawData如下图所示，行为基因名（symbol），列为样本名

导入分组信息表TrainGroup

TrainGroup <- read.csv("./data_group.csv", row.names = 1) # 为每个样本的分组信息（tumor和control）
colnames(TrainGroup) <- c('sample', 'group')

TrainGroup 如下图所示，第一列sample为样本名，第二列为样本对应的分组 （分组为二分类变量：disease和control）

导入要用于分析的基因HubGene (5个基因，这里用5个基因作为展示)

HubGene <- data.frame(symbol = c('VPS13D', 'MFF', 'ACSL1', 'VDAC1', 'PRELID1'))

HubGene 如下图所示，只有一列：5个基因的基因名

从TrainRawData中取出5个基因对应的表达矩阵，并且与之前准备的分组信息表TrainGroup进行合并

TrainData <- TrainRawData[HubGene$symbol, ] %>% t() %>% as.data.frame()
TrainData <- merge(TrainGroup, TrainData, by.x = "sample", by.y = 'row.names')

TrainData 如下图所示，第一列为样本名，第二列为分组情况，后面的都是基因表达量。

2. 2 构建列线图模型

创建数据分布对象，并设置为全局选项

在回归分析中，有时需要对连续变量进行标准化处理，以消除量纲差异对模型估计的影响，datadist 函数会计算数据集中每个连续变量的统计量，如均值、标准差、中位数、四分位数等，可以用于后续步骤中的变量标准化。

为什么要用datadist函数创建一个对象？

• 方便性： 将分布统计量保存在一个对象中，可以在后续的模型拟合过程中重复使用，而无需每次都重新计算.
• 一致性： 在多个模型拟合过程中使用相同的分布统计量，可以确保模型之间的一致性和可比性
• 自动化： rms 包中的许多函数（如 lrm、cph 等）都支持直接使用 datadist 对象来自动处理连续变量的标准化问题，从而简化了建模过程

创建数据分布对象后，通过options函数，设置为全局变量，以便在后续模型拟合中使用。（注意：这里如果不将datadist对象设置为全局变量，后续构建模型时会报错）

dd <- datadist(TrainData)
options(datadist = 'dd')

通过as.formula函数将要进行分析的分组以及基因转换为R的公式对象

## 准备拟合模型的公式
LrmFormula <- as.formula(paste0('group ~ ',
                  paste(HubGene$symbol,
                        sep = '',
                        collapse = '+')))

LrmFormula 如下图所示，group代表分组，波浪线后面的都是基因名称

根据公式拟合逻辑回归模型，formula参数指定了模型的公式，data 参数指定的整理好的数据框，maxit参数设置迭代算法的最大迭代次数，防止算法因无法收敛而无限循环。

## 准备拟合模型的公式
LrmModel <- lrm(formula = LrmFormula, # 回归模型的参数，指定自变量和因变量
                data = TrainData,  # 整理好的数据框
                maxit = 1000,
                y = TRUE,
                x = TRUE)

使用rms包中的nomogram函数来构建列线图

• fit = LrmModel —— 表示使用的是上一步拟合好的逻辑回归模型
• fun = plogis —— 这个参数指定了plogis函数（即exp(x) / (1 + exp(x))），它将log-odds转换为概率。这意味着诺莫图上的分数将直接对应于预测的疾病风险概率。
• funlabel = “Risk of disease” —— 这个参数用于指定列线图底部的标签
• lp = F —— 这个参数表示不显示线性预测值
• fun.at=c(0,.001,.5,.999,1) —— 这个参数指定了概率轴上的刻度位置

NomographModel <- nomogram(fit = LrmModel,  # 最佳模型
                    fun = plogis, # 进行logit转换
                    funlabel = "Risk of disease",
                    lp = F , # 不显示线性预测值
                    fun.at=c(0,.001,.5,.999,1)  # 概率坐标轴的范围和刻度
)

2. 3 列线图模型简单可视化

接下来一步就是要对列线图结果进行简单可视化，毕竟文字的展示效果不如图片更加直观。

plot(NomographModel, 
     xfrac = .35, # 变量与模型的占比（调整变量与坐标轴的距离）
     cex.var = 1.6,  # 变量字体加粗
     cex.axis = 1.4,  # 数轴：字体的大小
     tcl = -0.5, # 数轴：刻度的长度
     lmgp = 0.3, # 数轴：文字与刻度的距离
     label.every = 1,  # 数轴：刻度下的文字，1表示连续显示，2表示隔一个显示一个
     col.grid = gray(c(0.8, 0.95)))

列线图模型如下图所示， 图中最上方的单项得分Points，表示每个基因在不同取值下所对应的单项分数。图中图中下方的总得分Total Points，表示所有基因取值后对应的单项分数加起来合计的总得分。图中最下方的Risk of disease，表示样本患病的风险。

举个栗子：现在来了一个人，检测了这几个基因的表达水平，VPS13D基因表达水平为3左右，对应的单项得分往上对应的Points就是10左右；MFF基因表达水平为2.5左右，对应的单项得分同样往上拉一条线对应的单项Points也是10左右；依此类推，最后把每个基因对应的单项得分加起来，假如说是最后的Total Points是60，从60往下拉一条直线，对应的该受试者患病概率就是50%左右。

2. 4 列线图模型验证——校准曲线

构建完列线图模型之后，需要验证下构建出来的列线图预测效果是否准确，其中检验方式之一就是用校准曲线

先计算模型拟合优度（Goodness of Fit, GoF）的残差并提取分析结果对应的p值

• 模型拟合优度（Goodness of Fit, GoF） 是衡量统计模型对数据拟合程度的一个指标。它评估了模型预测值与实际观测值之间的接近程度。一个拟合优度高的模型意味着其预测值与实际观测值之间的差异较小，即模型能够很好地捕捉数据中的模式和关系。
• 残差（Residuals） 是观测值与模型预测值之间的差异。在回归分析中，残差是实际观测的响应变量值与模型根据自变量预测的响应变量值之间的差值，残差越大说明拟合出来的模型预测的准确性越差。

GofResidual <- stats::resid(LrmModel, "gof")
GofResidualPvalue <- signif(GofResidual[5], 3)

对前面构建的逻辑回归模型进行校准

• fit = LrmModel —— 表明对前面构建LrmModel模型进行校准评估
• method = “boot” —— 表明使用的是Bootstrap方法，这是一种通过重复从原始数据集中随机抽样（有放回）来估计统计量不确定性的技术。
• B = 1000 —— 指定了Bootstrap重复的次数，即1000次，为了确保校准结果准确

set.seed(888) # 用于设置随机数生成器的种子，以确保结果的可重复性
cal <- calibrate(LrmModel, method = "boot", B = 1000) # 使用calibrate函数对模型进行校准，使用方法是bootstrap， 重复次数为1000

2. 5 列线图模型验证——校准曲线（简单可视化）

plot(cal, lwd=2, lty=1, 
     cex.lab=1.4, cex.axis=1.4, cex.main=1.8, cex.sub=1.4, 
     xlim=c(0, 1), ylim= c(0, 1), 
     xlab="Nomogram-Predicted Probability", 
     ylab="Actual Probability", 
     col=c("#00468BFF", "#ED0000FF", "#42B540FF"),
     legend=FALSE)
lines(cal[, c(1:3)], type ="l", lwd=2, pch=16, col=c("#00468BFF"))
abline(0, 1, lty=3, lwd=2) 
legend(x=.6, y=.4, legend=c("Apparent", "Bias-corrected", "Ideal"), cex=1.2,
       lty=c(1, 1, 2), lwd = 2, col=c("#00468BFF", "black", "black"), bty="n")
text(x = 0.2, y = 0.8, paste0("Gof - Residual"),cex=1.0)
text(x = 0.4, y = 0.8, paste0("p = ", GofResidualPvalue),cex=1.0)

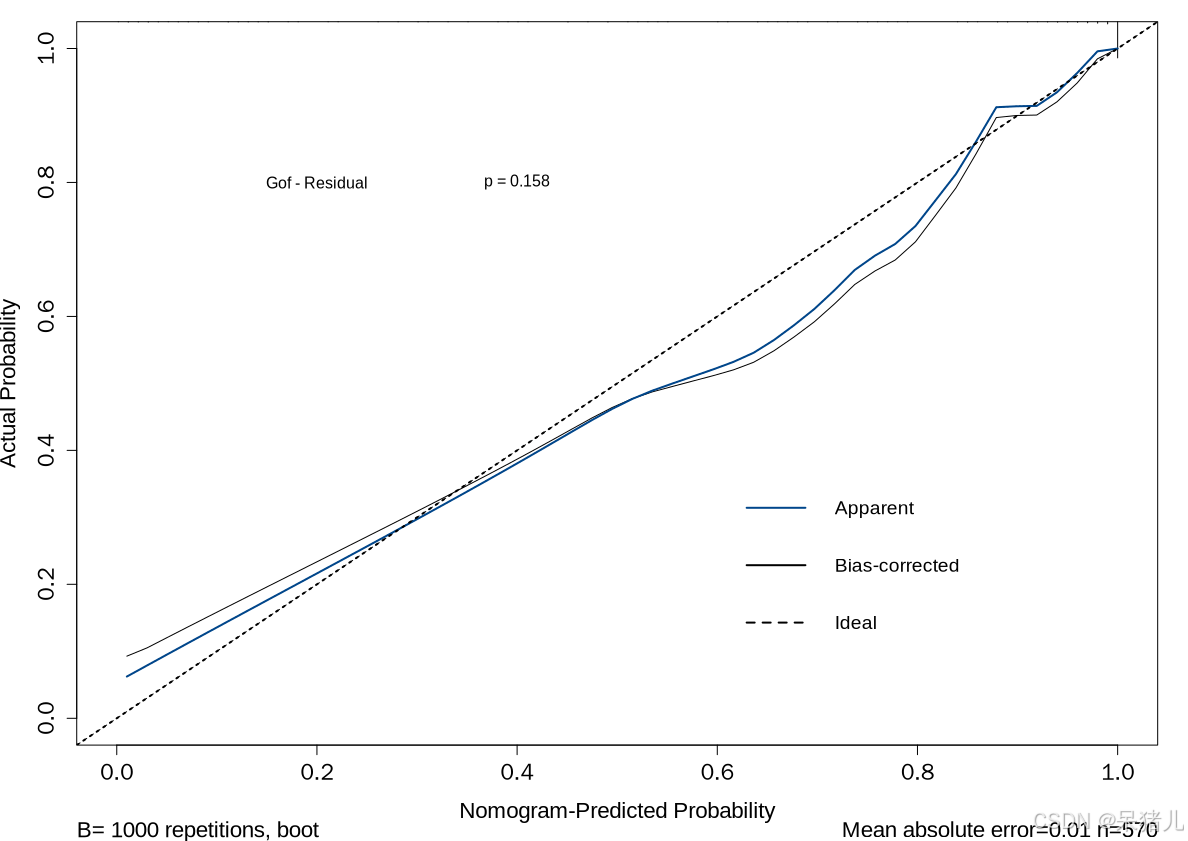
校准曲线如下图所示，Gof - Residual为计算的模型拟合优度残差，其原理在前面也介绍了，大致就是用于判断预测值与真实值之间的离散情况，如果p值大于0.05，则说明预测值与真实值之间并无非常明显的差异，模型拟合度较好。反之如果p值小于0.05，则说明预测值与真实值之间有着明显的差异，即说明模型拟合度较差。

横坐标表示列线图预测患病的概率，纵坐标表示患病的实际概率。黑色虚线表示完美预测。蓝色实线表示整个队列，黑色实线通过Bootstrapping（1000次重复）进行偏差校正，表示观察到的列线图性能，从结果中可以看到蓝色实现和黑色实线围绕黑色虚线，上下波动不大，说明虽然在预测过程中存在误差，但不是显著误差。

2. 6 列线图模型验证——ROC曲线

ROC（Receiver Operating Characteristic）分析是通过一系列不同的二分类方式（临界值或决定阈），计算诊断结果的真阳性率和假阳性率，以真阳性率（灵敏度）为纵坐标，假阳性率（1-特异度）为横坐标绘制的曲线，用曲线下面积（AUC）作为衡量预测准确性的指标。

在这里同样是使用ROC曲线来验证列线图模型预测准确性，先使用拟合的模型对原始数据或新数据进行预测

TrainData$predvalue <- predict(LrmModel, type="fitted")

之后用预测的值和分组信息计算AUC和95%CI

• response = TrainData$group —— 这个参数指定了真实的目标变量或类别标签，简单说就是想要预测的分组
• predictor = TrainData$predvalue —— 这个参数指定了要参与预测的变量，这里是上一步用拟合的模型与原始数据的预测值
• levels = c(‘control’, ‘disease’) —— 这个参数指定了response变量中类别的顺序，用于ROC曲线的计算。在这里，它告诉roc函数’control’是负类（或参考类），而’disease’是正类。（注意：这个levels非常重要，设置参考类如果反了，那么相应的结果也会是反的）

ModelROC <- roc(response = TrainData$group,
                predictor = TrainData$predvalue,
                levels = c('control', 'disease'))
ModelROC$auc

ModelROC$auc如下图所示，表明曲线下面积（Area under the curve, AUC）为0.9852（AUC越接近于1表明预测准确性越高）。

2. 7 列线图模型验证——ROC曲线（简单可视化）

接下来一步就是要对ROC分析结果进行简单可视化，毕竟文字的展示效果不如图片更加直观。

plot(ModelROC, 
     main = paste0("ROC Curve for Disease Prediction of ", colnames(TrainData)[1]), # 设置主标题
     col = "#DD7123", # 设置曲线颜色
     lwd = 2,  # 线条宽度
     print.auc = T, # 打印AUC的值
     print.auc.x = 0.4, # AUC值得位置（x轴）
     print.auc.y = 0.5, # AUC值得位置（y轴）
     print.auc.pattern = 'AUC=%.3f', # AUC值得格式，表明保留三位小数
     print.auc.cex = 1.2,  # AUC值字体大小
     grid = c(0.5,0.2), # 网格线设置
     grid.col = "gray", # 网格线颜色
     xlab = "False Positive Rate (1 - Specificity)",  # x轴标签  
     ylab = "True Positive Rate (Sensitivity)",  # y轴标签 
     font.lab = 2,  # 轴标签字体样式  
     cex.axis = 1.2,  # 轴标签字体大小  
     cex.main = 1.5  # 主标题字体大小  
)

ROC曲线如下图所示

• 横坐标 —— 假阳性率（False Positive Rate, FPR），也称为1-特异性或误报率。它表示在所有实际为阴性的样本中，被错误地判断为阳性的比例。FPR的值越接近0，说明模型的误报率越低，即模型在判断为阳性的样本中，真正为阴性的样本占比越少。
• 纵坐标 —— 真阳性率（True Positive Rate, TPR）：也称为敏感度或真正率。它表示在所有实际为阳性的样本中，被正确地判断为阳性的比例。TPR的值越接近1，说明模型的敏感度越高，即模型能够准确地识别出更多的真正阳性样本。
• 曲线位置 —— ROC曲线越靠近左上角（FPR越小，TPR越大），说明模型的预测准确率越高，这是因为左上角的点代表了最低的误报率和最高的真正率。
• 曲线下面积（AUC） —— AUC值用于量化地表示模型的预测准确性。AUC值越高，说明模型的预测性能越好。当AUC值等于0.5时，表示模型没有预测价值（即随机猜测）；当AUC值大于0.7时，通常认为具有较高的诊断价值。

通常构建的列线图模型都要经过校准曲线和ROC曲线分析才能验证模型预测的准确性，如果单独使用列线图模型可信度不高。

---

---

3. 结语

以上就是零基础入门转录组数据分析——列线图模型（诊断）的所有过程，如果有什么需要补充或不懂的地方，大家可以私聊我或者在下方评论。

如果觉得本教程对你有所帮助，希望广大学习者能够点赞，收藏，加关注

关于我们： 我们的团队是领航生信，如果大家想要系统学习常规SCI生信套路和流程或者了解更多生信相关知识，可以在下方公众号链接找到我们~~~

祝大家能够开心学习，轻松学习，在学习的路上少一些坎坷~~~

---

• 目录部分跳转链接：零基础入门生信转录组数据分析——导读