计算方法（）

第一节：

非线性方程和方程组的数值解法

求根步骤：

二分法：

 

迭代法： 

收敛性、收敛速度：

计算效率：

 收敛阶，即一次计算能收敛到上一次的p次方。 

---

单点迭代法：

单点迭代法的收敛阶： 

注意：这里P至少是2，因此不可以通过这个定理的出“至少是线性收敛”之类的结论。 

---

牛顿迭代法：

牛顿法的局部收敛性：

牛顿法的改进：

牛顿下山法：

---

多点迭代法：

局部收敛性和收敛速度：

---

重根迭代法：

---

---

第二节：

线性方程组解法

基本解法：

向量范数：

常用的向量范数：

---

矩阵范数：

 常用的矩阵范数：

 谱半径：

---

 高斯消元法： 

 类似的消元法：Gauss-Jordan消元法

列选主元（素）消元法：

全主元素消元法：

---

---

第三节：

P为进行行变换的单位阵。

---

Doolittle分解：

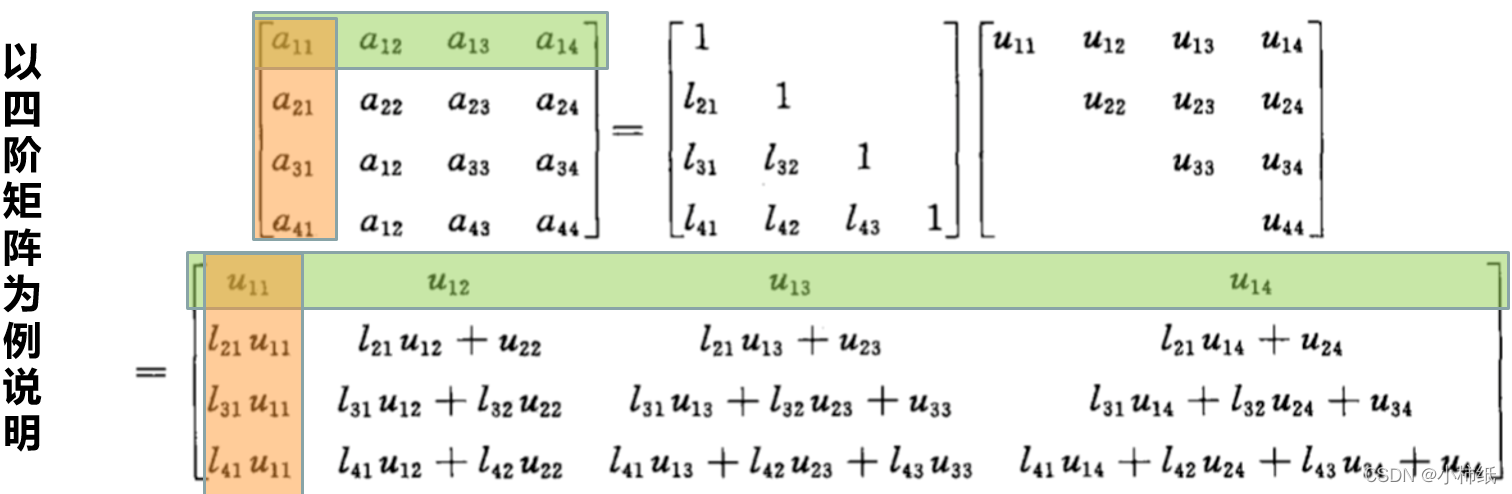
推导公式：

注意：先求U行，再求L列。

求解实例：

---

 Crout分解：（与Doolittle分解对称）

求解实例：

---

Cholesky分解（平方根法）：

 推导过程：

 改进的Cholesky分解方法： 

---

追赶法：

使用追赶法的条件：

即中间元素大于两边元素绝对值和。

过程：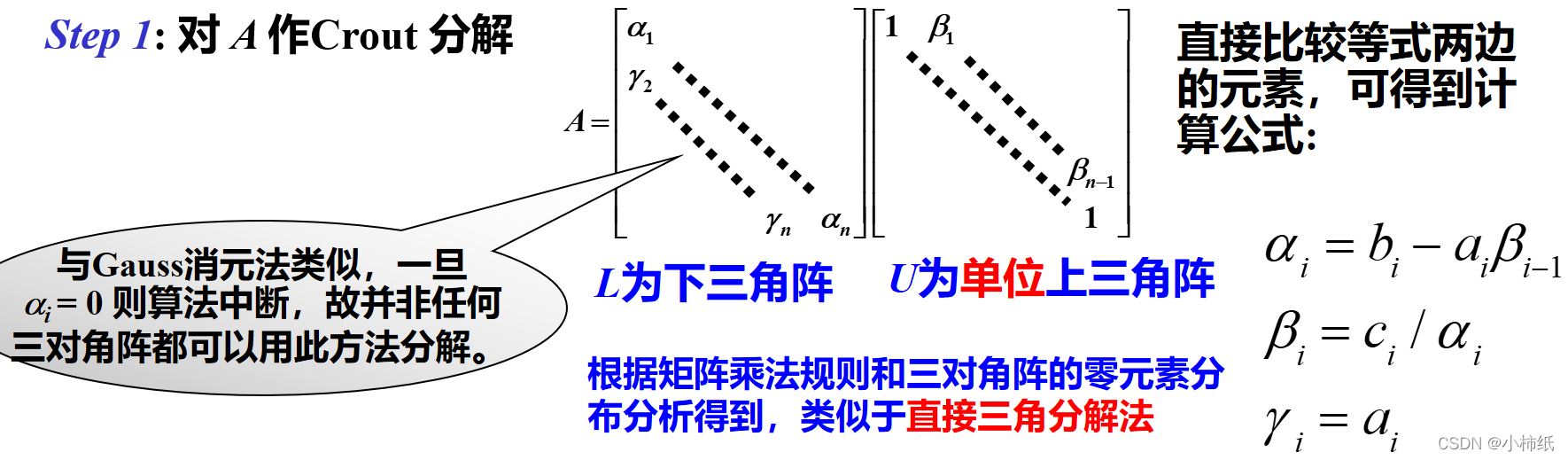

 实质是高斯消去法应用于三对角方程。

---

误差分析：

A的条件数 cond(A) :

判断矩阵是否病态：

---

---

第四节：

线性方程组的迭代解法：

迭代公式有效条件：

（1）收敛性：

（2）相容性：

---

Jacobi迭代：

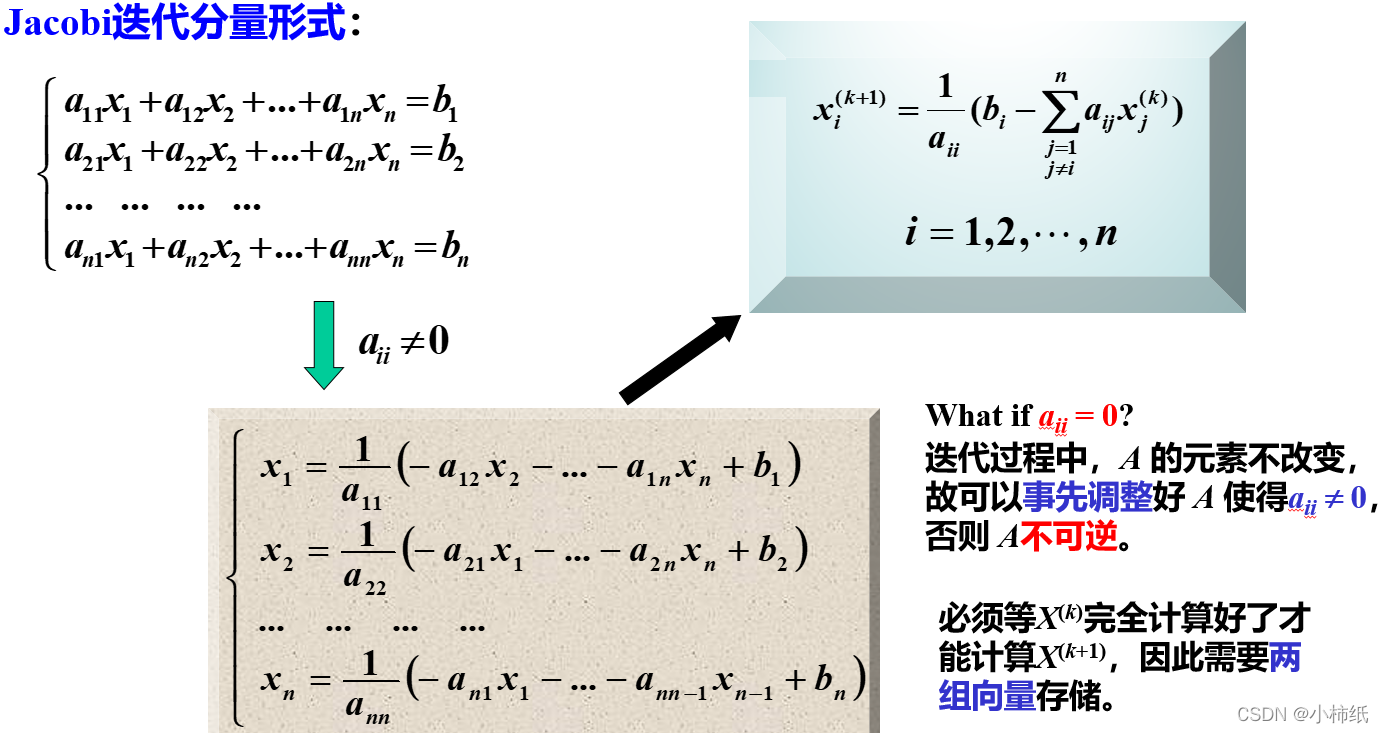
Gauss - Seidel迭代：

注意：以上两种方法存在收敛性问题：

超松弛迭代法（SOR方法）： 

---

迭代收敛的其他判别方法：

---

---

第五节：

插值法：

---

Lagrange插值公式： 

 常用公式：

 截断误差：

---

等距节点公式：

性质：

差分在牛顿公式中的引用：

---

由于单一公式带来的不稳定性，引入分段插值：

---

---

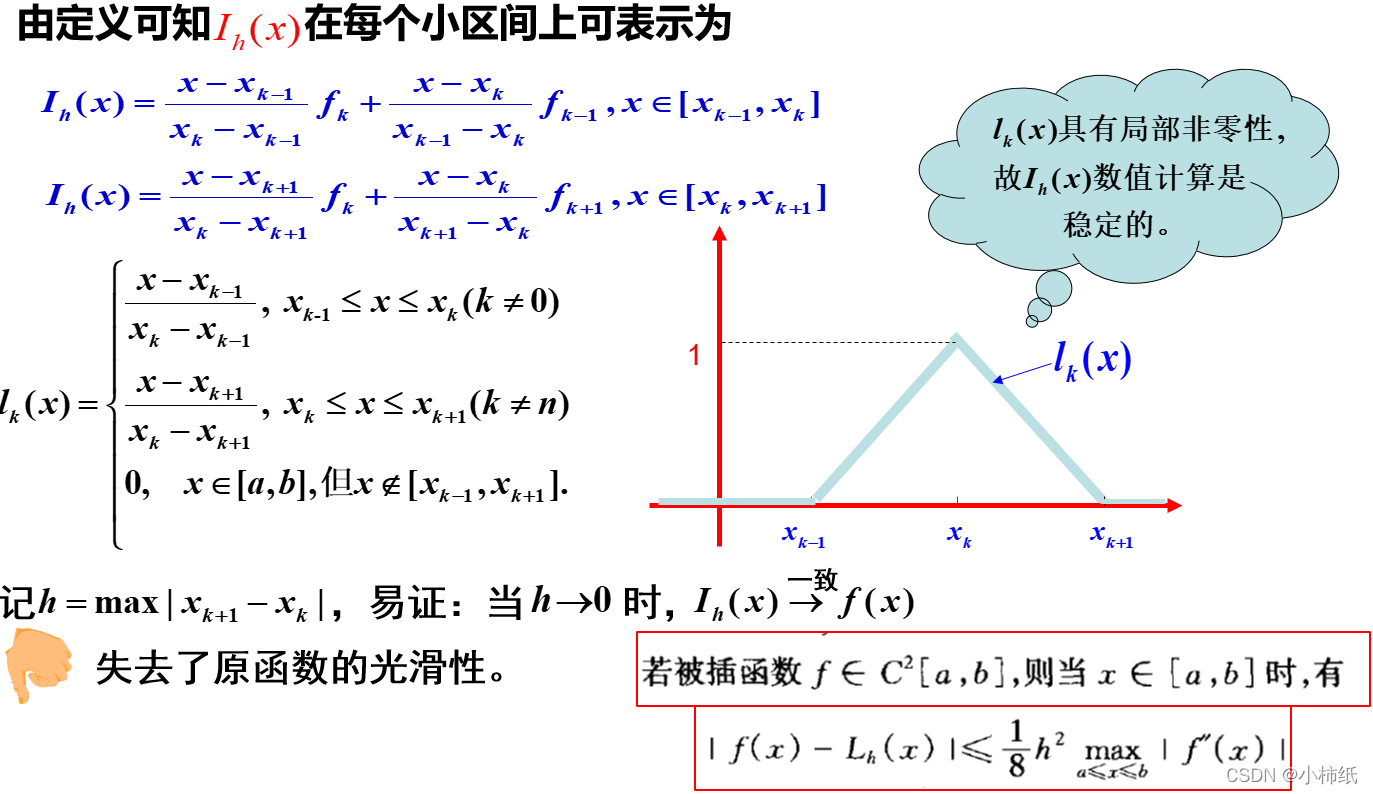
 第六节：

最佳平方逼近：

---

常见的正交多项式：

勒让德（Legendre）多项式：

切比雪夫（Chebyshev）多项式：

判断函数族线性无关：

---

最佳平方逼近问题解法：

法方程组：

---

正交基底的用途——正交多项式族做平方逼近：

当区间为[-1, 1]时：

---

曲线拟合的最小二乘逼近：

最小二乘拟合多项式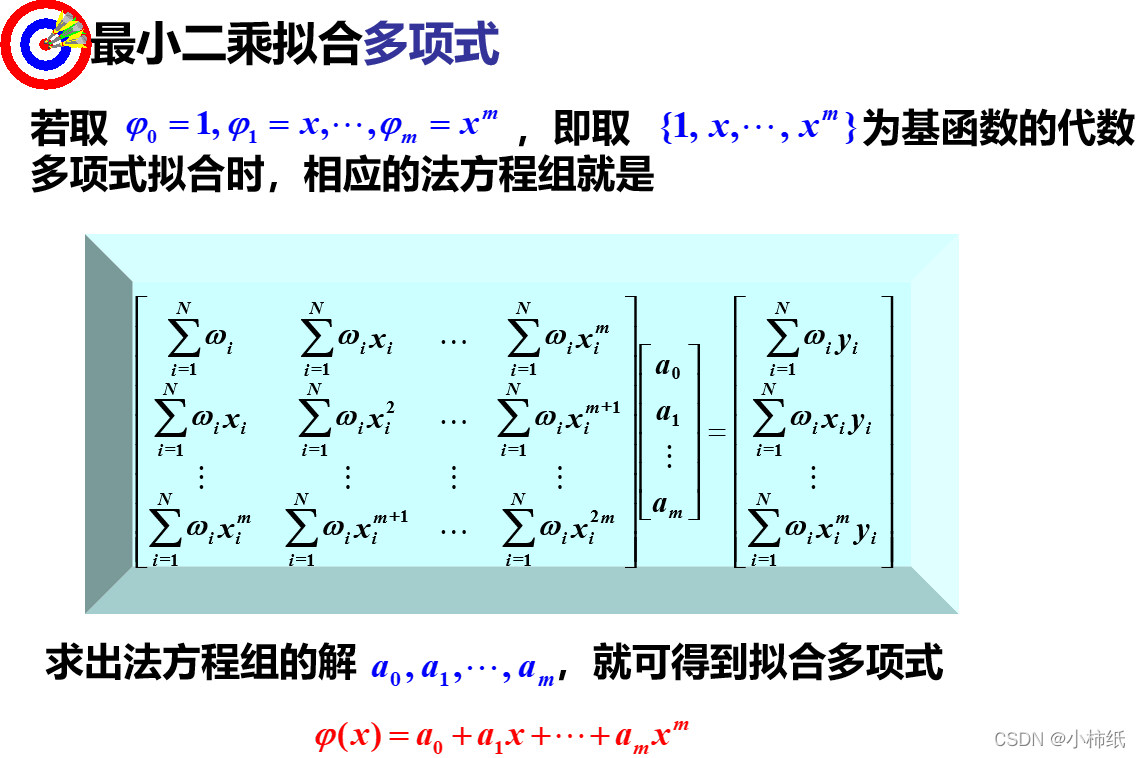： 使用实例：

---

---

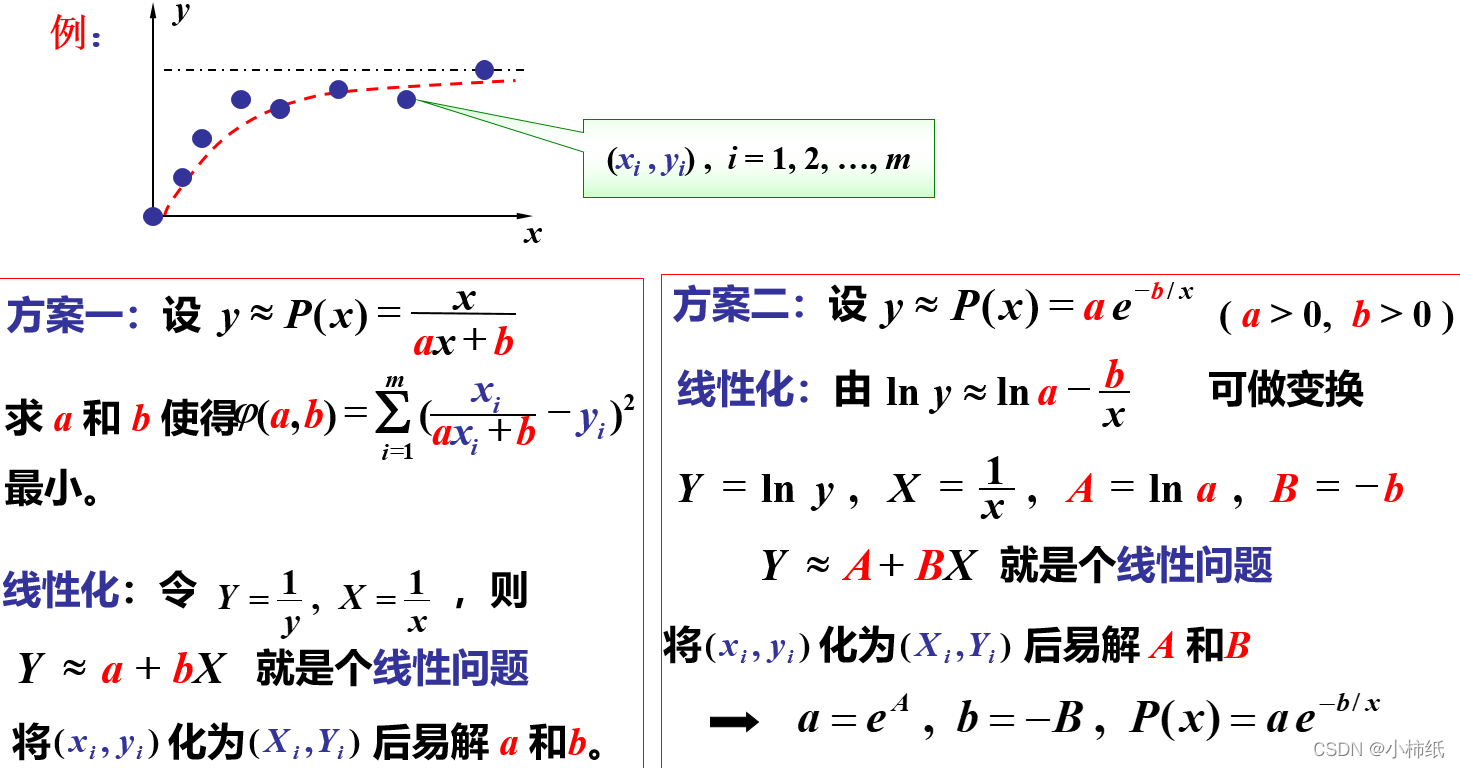
第七节：

数值积分求法思想：

代数精度与插值型求积公式：

求积公式的构造：

余项（误差）：

求法实例：

---

等距节点的Newton-Cotes公式：

求法与余项（误差）：

求法实例：

稳定性：余项求法：

复化的Newton-Cotes 公式：

---

---

第八节：

常微分方程初值问题：

---

常用解法：

离散化方法：

 实质：

 相当于泰勒展开只展开了一项，简便的同时误差会扩大。

---

线性多步法：

泰勒展开思路：

相容：

待定系数法：r(也就是你要通过这个方法计算多高次数的方程)会影响到底有没有解。超过2p+2了就没有，等于2p+2就有一个，小于2p+2就可以有多个解，系数更加自由。

---

线性多步法的收敛性：

特征多项式：

根条件：