特殊规划问题——运输问题

运输问题

运输问题，一类具有特殊结构的线性规划问题。由于运输问题约束方程组的系数矩阵是完全幺模的，即所有的子行列式为0或±1，存在着比单纯形法更简单的特殊解法。

现已发现的运输型问题有以下6类：
一般运输问题，又称希契科克运输问题，简称H问题。
网络运输问题，又称图上运输问题，简称T问题。
最大流量问题,简称F问题。
最短路径问题，简称S问题。
任务分配问题，又称指派问题,简称A问题。
生产计划问题，又称日程计划问题，简称CPS问题。
如把产地称为源（发点），销地称为汇(收点)，则任务分配问题、生产计划问题等运输型问题的模型也可以归纳成类似上述形式。

〇、 前言（问题提出）

运输问题的典型情况是研究单一品种物质的运输调度问题：设某种物品有$m$个产地$A1，A2，\cdot \cdot \cdot ，Am$，各产地的产量分别是$a1，a2，\cdot \cdot \cdot ，am$；有$n$个销地$B1，B2，\cdot \cdot \cdot ，Bn$，各个销地的销量分别为$b1，b2，\cdot \cdot \cdot ，bn$。假定从产地$Ai(i=1,2,\cdot \cdot \cdot ,m)$向销地$Bj(j=1,2,\cdot \cdot \cdot ,n)$运输单位物品的运价为$c_{ij}$，问怎么调运这些物品才能使总运费最小？

一、 运输问题及其数学模型

·运输问题的数学模型

产销平衡运输问题的数学模型可表示如下：

式中min表示求极小值，因为目标函数表示运输总费用，要求其极小化，S.T.表示“约束条件为”。约束条件中前m行的意义是由某一个产地$A_i$运往各个销地的物品数量$x_{ij}$之和等于该产地的产量$a_i$，后n行的意义是由某一个产地Bj运往各个销地的物品数量$x_{ij}$之和等于该销地的销量$b_i$，最后一行表示变量非负约束，因为物品为负数无意义。
如果运输问题的总产量等于总销量，即有当${ɑ}_i$，$b_j$满足此条件时称为产销平衡的运输问题，否则称为产销不平衡的运输问题。产销不平衡的运输问题可以通过增加假想产地或假想销地，化成产销平衡的运输问题。
以上模型是一种线性规划模型，单纯形法师求解线性规划问题十分有效的一般方法，因而单纯形法也可以求解运输问题。但是采用线性规划的单纯形法求解运输问题时，先得在每个约束条件中引入一个人工变量，即使求解3个产地，4个销地$(m=3,n=4)$这样的简单运输问题，在不考虑去掉多余约束条件的情况下，变量数目也会达到19个之多，因而需要寻求更简便的解法。

·产销平衡运输问题数学模型的特点

由于运输问题的结构和性质，使其具有以下几个特点：

1. 运输问题有有限最优解

对产销平衡的运输问题，可以找到一个可行解：其变量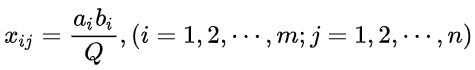
是运输问题的一个可行解，其中，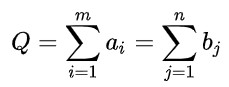
目标函数有下界0，目标函数值不会趋于负无穷 。由此可知，运输问题必存在有限最优解。

2. 运输问题约束条件的系数矩阵

将约束条件的结构加以整理，可知运输模型约束方程组的系数矩阵具有下述比较松散且特殊的形式：

其系数列向量的结构式：$A_{ij}=(0,\cdot \cdot \cdot ,0,1（第i个）,0,\cdot \cdot \cdot ,0,1（第m+j个）,0,\cdot \cdot \cdot ,0{)}^T$，即除第i个和第$(m+j)$个分量为1外，其他分量全等于0。这是$(m+n)\times mn$的矩阵，每一列的元素中只有2个1，其余均为0。可以证明$A的秩=(m+n－1)$，所以运输问题的任一基本可行解都有$(m+n-1)$个基变量，这$(m+n-1)$个基变量的值就对应一个调运方案。

由此可知，运输问题的约束条件具有下述特点：
（1）运输问题的有$m\times n$个变量，$(m+n)$个约束方程，$(m+n-1)$个基变量。
（2）约束条件系数矩阵的元素等于0或1。
（3）约束条件系数矩阵的每一列有两个非零元素，这对应于每一个变量在（4）前m个约束方程出现一次，在后n个方程中也出现一次。
对产销平衡运输问题，除上述两个特点外，还有以下特点：
（1）所有结构约束条件都是等式约束。
（2）各产地产量之和等于各销地销量之和。

3. 约束条件系数矩阵的每一列有两个非零元素，这对应于每一个变量在前m个约束方程中出现一次，在后n个约束方程中也只出现一次。

二、 用表上作业法求解运输问题

可以参考这篇博客的图解过程：
CSDN博主「健康平安的活着」的原创文章
原文链接：https://blog.csdn.net/u011066470/article/details/103929824

三、 运输问题的进一步讨论

其实表上作业法的收敛速度是不快的，而且初始化对迭代速度的影响是比较大的。那么有一种表上作业法的优化方法：$Vogel$法，利用罚数来加快迭代速度，可以得到更快的最优解。
可以参考：
CSDN博主「奥伊米亚慷」的原创文章
原文链接：https://blog.csdn.net/m0_46927406/article/details/109903843

如果遇到产销不平衡问题，我们又应该如何解决呢？
其实也很好办，如单纯性法的思想，用我自己的话来说就是“缺啥补啥”！
产量大于销量，那么销量不够，我幻想有一个销售商，可以销售这些剩余产品；销量大于产量，那么产量不够，我幻想有一个产商，可以生产补足销售的产品。
所以，如单纯形法的解题思路一样，需要我们自行添加人工变量，再进行表上作业法即可。

四、 应用（代码实现）

欢迎参考后期发出的《线性规划的实例赏析》中的例题【二】。
链接：https://blog.csdn.net/weixin_51128278/article/details/117999175

五、 总结

由于运输问题在数学建模中出现的情况很少见，而且算是一类比较简单的问题，那么在此就多参考了一些优秀博主的文章，做一个总结和分享。对博主表示相当感谢！

六、 参考

《运筹学教程》胡运权