Map和Set/二分搜索树

map和set概念

Map:存储Key-value键值对，存储的数据是映射关系，需要根据不重复的key对应value.
Set:存储不重复元素的线性表，只判定元素是否存在，或者过滤重复元素.
Map和Set是一种专门用来进行搜索的数据结构，是一种适合动态查找的集合容器；用它来进行遍历操作效率极低。

• Key-Value键值对
  Key:搜索的数据(关键字）
  Value:和关键字相对应（值）
  Map中存储的是键值对，而Set中只存储Key.

Map的使用

迭代器：用于遍历集合，有了for-each循环，在不需改原集合的前提下，直接用for-each循环即可。只有需要修改原集合的内容，才会用到迭代器。

关于Map的说明

Map是一个接口类，该类没有继承自Collection，该类中存储的是<Key,Value>结构的键值对，并且Key一定是唯一的，不能重复。
Map集合内部元素之间的先后顺序与插入顺序关系不大。

关于Map集合的常用操作

操作	方法
添加元素	put( Key,Value)
根据Key取得Value	get(Key)
根据Key取得Value	getOrDefault(Object key, V defaultValue)
删除操作	remove(Object key)
遍历Key的不重复集合	Set KeySet()
遍历Value的不重复集合	Collection Values()
返回所有Key-Value的映射关系	Set<Map.Entry<K, V>> entrySet()
查询是否包含Key	boolean containsKey(Object key)
查询是否包含Value	boolean containsValue(Object Value)

代码示例：

public static void main(String[] args) {
        Map<String, String> map = new HashMap<>();
        //添加元素
        map.put("周杰伦", "告白气球");
        map.put("陈奕迅", "富士山下");
        map.put("林俊杰", "她说");
        map.put("沈以诚", "告白");
        System.out.println(map.put("林俊杰","手心的蔷薇"));
        System.out.println(map);
        //查找成功
        System.out.println(map.get("林俊杰"));

        //查找不成功返回null
        System.out.println(map.get("彭于晏"));
        //删除元素
       System.out.println(map.remove("周杰伦","告白气球"));
        System.out.println(map);

运行结果：

遍历操作 （遍历Key的不重复集合/遍历Value的不重复集合 ）
有遍历Map集合，就需要把Map集合转为Set集合，然后进行遍历操作，

 public static void main(String[] args) {
        Map<String, String> map = new HashMap<>();
        //添加元素
        map.put("周杰伦", "告白气球");
        map.put("陈奕迅", "富士山下");
        map.put("林俊杰", "她说");
        map.put("沈以诚", "告白");
         //获取map中所有key值
        //快捷生成临时变量 ，接收返回值 Alt+Enter
        Set<String> strings = map.keySet();
        //获取map中所有的value值
        Collection<String> values = map.values();
        System.out.println(strings);
        System.out.println(values);
    }

二分搜索树

向BST中添加元素——add(int value）

1.若该二分搜索树为空树，则返回null；
2.若该二分搜索树不为空，则按照逻辑确定插入元素的位置，在此插入新节点。

 //向BST中添加一个新元素
    public void add(int value) {
        root = add(root, value);
    }

    //向以root为很节点得的BST中添加一个新元素value，返回添加元素后的根节点
    private Node add(Node root, int value) {
        //当root为空时，此时走到叶子节点，创建新节点并插入值
        if (root == null) {
            root = new Node(value);
            size++;
            return root;
        }
        //比较根节点和value的大小
        if (value < root.val) {
            //连接
            root.left = add(root.left, value);

            return root;
        }
        //连接
        root.right = add(root.right, value);
        return root;
    }
        //打印
    public String toString() {
        StringBuilder sb = new StringBuilder();
        generateBSTString (root,0,sb);
       return sb.toString();
    }
    //先序遍历二分搜索树，将根节点，树的深度，
    private void generateBSTString(Node root,int depth,StringBuilder sb){
        if(root == null){
            sb.append(generateBSTDepth(depth)).append("null\n");
            return;
        }
        //先访问根节点
        sb.append(generateBSTDepth(depth)).append(root.val).append("\n");
        //递归访问左子树
         generateBSTString(root.left,depth+1,sb);
        //递归访问右子树
         generateBSTString(root.right, depth+1, sb);
    }

    //打印当前BST的深度，每进入下一层就多两个--
    private String  generateBSTDepth(int depth){
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < depth; i++) {
            sb.append("--");
        }
        return sb.toString();
    }

测试

 public static void main(String[] args) {
        BST bst = new BST();
        int[] data={5,10,7,3,6,2,8};
        for (int i = 0; i < data.length; i++) {
            bst.add(data[i]);
        }
        bst.add();
        System.out.println(bst);
        }

向BST中查找元素——boolean contains(int val)

返回BST的最小值(在左树）：root.left = null;
返回BST的最大值（在右树）：root.right= null;

查找指定元素

//查找操作，判断以root为根节点的二叉搜索树是否存在指定元素
    
  public boolean contains(int val){
        return contains(root,val);
  }
    
    private boolean contains(Node root, int val) {
    if(root == null){
        return false;
        //根节点就是待查找元素
    }else if(root.val == val)return true;
       //在左树中查找
    else if(val<root.val)return contains(root.left,val);
      //在右树中查找
    return contains(root.right, val);
    }

测试

 public static void main(String[] args) {
        BST bst = new BST();
        int[] data={5,10,7,3,6,2,8};
        for (int i = 0; i < data.length; i++) {
            bst.add(data[i]);
        }
            bst.add(1);
       System.out.println(bst.contains(7));
       System.out.println(bst.contains(4));
       System.out.println(bst.contains(11));
    }

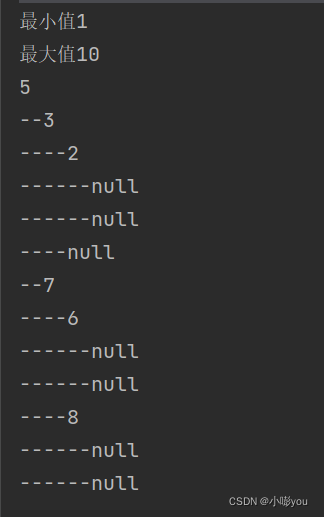
测试结果

查找bst中的最大最小值

public int maximum() {
        if (size == 0) {
            throw new NoSuchElementException("bst is empty!");
        }

        Node maxNode = maximum(root);
        return maxNode.val;
    }

    //找到以root为根节点的BST中的最大值
    private Node maximum(Node root) {
        if (root.right == null) {
            return root;
        }
        return maximum(root.right);
    }
    //找到以root为根节点的BST中的最小值

    public int minimum() {
        if (size == 0) {
            throw new NoSuchElementException("bst is empty!");
        }
        Node minNode = minimum(root);
        return minNode.val;
    }

private Node minimum(Node root){
        if(root.left == null){
            return root;
        }
        return minimum(root.left);
}

测试结果

删除元素

删除最大值
最大值的右孩子为空，则只需要把最大值的左子树连接就好
删除最小值
最小值的左子树为空，则只需要把最小值的右孩子连接就好

    //删除最小值节点，并返回其val
    public int removeMin() {
        int min = minimum();
        root = removeMin(root);
        return min;
    }

    //删除当前以root为根节点的bst中的最小值,返回删除后的根节点
    private Node removeMin(Node root) {
        if (root.left == null) {
            //说明此时root为当前bst的最小值
            //将右树连接即可
            Node right = root.right;
            //断开原来的连接
            root.right = null;
            size--;
            return root.right;
        }
        //连接
        root.left = removeMin(root.left);
        return root;
    }

    //删除最大值节点，返回其val
    public int removeMax() {
        int max = maximum();
        root = removeMax(root);
        return max;
    }

    //删除当前以root为根节点的bst中的最大值
    private Node removeMax(Node root) {
        if (root.right == null) {
            //说明此时root为当前bst的最大值，将左树连接即可
            Node left = root.left;
            //断开原来的连接
            root.left = null;
            size--;
            return left;
        }
        //连接
        root.right = removeMax(root.right);
        return root;
    }

删除任意节点
1.待删除节点为空
2.待删除节点只有一个孩子（类似于删除最大或最小值）
3.待删除结点有左右孩子
找到待删除节点的前驱节点或者后继节点，让它来代替带删除元素，做删除后的原位置的树根，这个前驱或者后继节点Node一定满足：所有左树节点值<Node<所有右树节点值

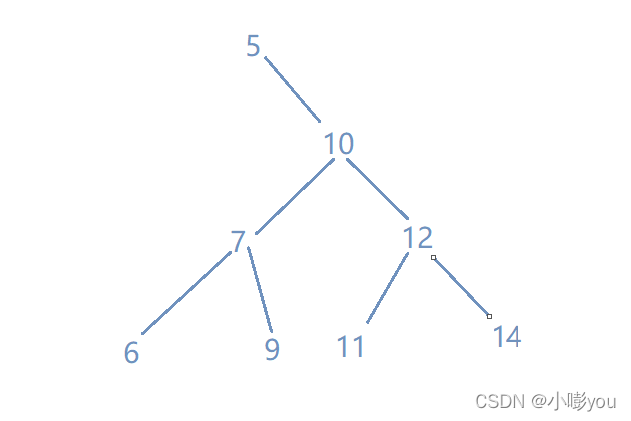
1.先找到10的后继节点11；
2.在右子树中删除最小值11；
3.将10的左子树连接到11的左孩子，11的右子树连接删除后右子树中的最小值；
4.将原来10所有的指向关系断开，返回删除后的新的树根11.
此时11是右子树的最小值，则它小于右子树的所有结点，因为它在右子树，所以它的值大于左子树的所有值。因此选它作为新树根。
删除10之后的BST如图：