2、 带权图的最小生成树(设计实验【必做】)
以lab5_2.cpp为基础,参考课本189页-191页的内容,以邻接矩阵为存储结构,实现的无向带权图的最小生成树算法Prim。请把答案代码直接补充在源文件中。以课本190页图6-16为例,其输入和输出样张如下图所示。
我模仿前辈的,其中源文件里面的源代码有些更改了,而且,prim算法和课本上的也有些不一样,懵懵懂懂的
#include <iostream>
using namespace std;
const int MaxSize = 10; //图中最多顶点个数
int visited[MaxSize]={0}; //初始化所有的点都为0,表示未访问
const int MAX = 1000;
struct element //用结构体数组来表示lowcost数组(权值)、adjvex数组(最短边邻接点)
{
int lowcost, adjvex;
};
int MinEdge(element *e, int vertexNum);//声明函数,e:传进lowcost数组
template <class DataType>
class MGraph
{
public:
MGraph(DataType a[ ], int n, int e); //构造函数,建立具有n个顶点e条边的图
~MGraph( ) { } //析构函数为空
void DFSTraverse(int v); //深度优先遍历图
void BFSTraverse(int v); //广度优先遍历图
void Prim(int v);
private:
DataType vertex[MaxSize]; //存放图中顶点的数组
int arc[MaxSize][MaxSize]; //存放图中边的数组
int vertexNum, arcNum; //图的顶点数和边数
};
template <class DataType>
MGraph<DataType>::MGraph(DataType a[ ], int n, int e)
{
int i, j, w;
vertexNum=n; arcNum=e;
for (i=0; i<vertexNum; i++)
vertex[i]=a[i];//输入每个点表示的字母,即ABCDEF等等
for (i=0; i<vertexNum; i++)
for (j=0; j<vertexNum; j++)
arc[i][j]=MAX;//初始化每个边的权值
for (int k=0; k<arcNum; k++)
{
cout<<"请输入边的两个顶点的序号:";
cin>>i;
cin>>j;//输入边依附的两个顶点的编号
cout<< "请输入边的权值:";
cin>>w;
arc[i][j]=w; arc[j][i]=w;
}
}
template <class DataType>
void MGraph<DataType>::DFSTraverse(int v)
{
cout << vertex[v]; visited[v] = 1;//表示已访问
for (int j = 0; j < vertexNum; j++)
if (arc[v][j] != MAX && visited[j]==0)//如果与v相连的j点未被访问,则访问遍历j点
DFSTraverse(j);
}
//广度优先遍历
template <class DataType>
void MGraph<DataType>::BFSTraverse(int v)
{
int w,Q[MaxSize];
int front = -1, rear = -1; //初始化队列,假设队列采用顺序存储且不会发生溢出
cout << vertex[v]; visited[v] = 1; Q[++rear] = v; //被访问顶点入队
while (front != rear) //当队列非空时
{
w = Q[++front]; //将队头元素出队并送到v中
for (int j = 0; j < vertexNum; j++)
{
if (arc[w][j] != MAX && visited[j] == 0 ) {
//存在与w点相连的j点且j点未被访问过 则输出j点值 然后标记j点将j点入队
cout << vertex[j];
visited[j] = 1;
Q[++rear] = j;
}
}
}
}
//算法输入
template <class DataType>
void MGraph<DataType>::Prim(int v)
{
int i, j, k;
element e[MaxSize];//定义结构体,里面是所有邻接点的权值
for(i=0; i<vertexNum;i++)
{
e[i].adjvex = v;
e[i].lowcost = arc[v][i];//把边的权值赋值上去
}
e[v].lowcost = 0;//访问到的该边权值就取消,记为0,不再访问
// int adjvex[MaxSize], lowcost[MaxSize];
// lowcost[0]=0,adjvex[0]=0;
//初始化辅助数组
// for(i = 1; i < vertexNum; i++)
// {
// lowcost[i] = arc[0][i];
// adjvex[i] = 0;
// }
// lowcost[0] = 0;//将顶点v加入集合U
for(k = 1; k <vertexNum; k++)
{
j = MinEdge(e, vertexNum); //寻找最短边的领接点j
cout<< "<" <<e[j].adjvex << "," << j << ">" << e[j].lowcost <<endl;
e[j].lowcost = 0;//将顶点j加入集合U
//调整辅助数组
for(i = 0; i <vertexNum; i++)
{
if(arc[i][j] < e[i].lowcost)
{
e[i].lowcost = arc[i][j];
e[i].adjvex = j;
}
}
}
}
int MinEdge(element *e, int vertexNum)
{
int min = 10000;
int k = 0;
for(int i = 0; i <vertexNum; i++)
{
if((min > e[i].lowcost) && (e[i].lowcost!=0))//如果邻边权值小,而且没被访问过
{
k = i;
min = e[i].lowcost;
}
}
return k;
}
int main( )
{
char ch[]={'A','B','C','D','E','F'};
MGraph<char> MG(ch, 6, 9);
for (int i=0; i<MaxSize; i++)
visited[i]=0;
cout<<"深度优先遍历序列是:";
MG.DFSTraverse(0);
cout<<endl;
for (int i=0; i<MaxSize; i++)
visited[i]=0;
cout<<"广度优先遍历序列是:";
MG.BFSTraverse(0);
cout<<endl;
cout<<"最小生成树的生成过程为:"<<endl;
MG.Prim(0);
cout<<endl;
system("pause");
}
成果如下:
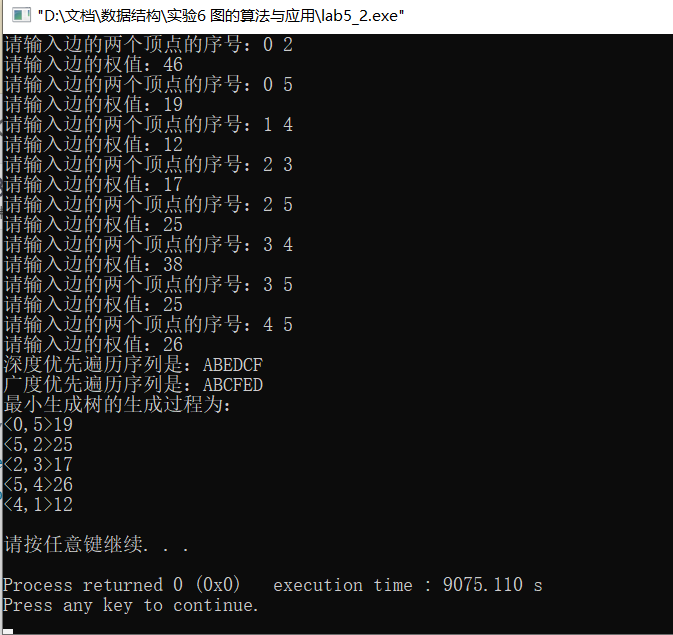








 这篇博客介绍了一种基于邻接矩阵的无向带权图最小生成树算法Prim的实现。作者使用C++编程语言,以lab5_2.cpp为起点,参照教材中的内容,创建了一个MGraph类模板,包含了构造函数、深度优先遍历、广度优先遍历和Prim算法。在Prim算法中,作者通过维护一个结构体数组来表示边的权值和邻接点,并实现了寻找最小边的辅助函数MinEdge。博客提供了输入输出示例,展示了算法如何找到图的最小生成树。
这篇博客介绍了一种基于邻接矩阵的无向带权图最小生成树算法Prim的实现。作者使用C++编程语言,以lab5_2.cpp为起点,参照教材中的内容,创建了一个MGraph类模板,包含了构造函数、深度优先遍历、广度优先遍历和Prim算法。在Prim算法中,作者通过维护一个结构体数组来表示边的权值和邻接点,并实现了寻找最小边的辅助函数MinEdge。博客提供了输入输出示例,展示了算法如何找到图的最小生成树。

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








