字符串和多维数组学习笔记(21.10.20)

简单的就不写了，以下只总结重点内容。

---

字符串

一、模式匹配

1.定义：给定主串S="s1s2…sn"和T=“t1t2…tm”，在主串S中寻找T的过程称为模式匹配，T称为模式。如果匹配成功，返回T在S中的位置，否则返回0。
2.方法：BF算法和KMP算法。

BF算法

从主串S的第0个字符开始和T的第0个字符进行比较，若相等，继续比较两者后续字符；否则，主串S下一个字符和T第0个字符比较。
若T中的字符全部比较完毕，匹配成功，S的字符全部比较完，匹配失败。
过程如下：

int BF(char S[],char T[])
{
    int start=0;
    int i=0,j=0;
    while((S[i]!='\0')&&(T[j]!='\0'))
    {
        if(S[i]==T[j])
        {
            i++;
            j++;
        }
        else
        {
            start++;
            i=start;
            j=0;
        }
    }
    if(T[i]=='\0')
        return start+1;
    else return 0;
}

BF算法匹配不成功时存在大量回溯，时间性能低。

设串S长度为n，串T长度为m，在匹配成功的情况下，考虑两种极端情况：

• 最好：不成功的匹配都发生在串T的第一个字符。
  ${\sum }_{i=1}^{n-m+1}{P}_i(i-1+m)$=$\frac{(n+m)}{2}$=O(n+m)
  ( P_i 表示在第i个位置上匹配成功的概率，P_i=$\frac{1}{n-m+1}$）
  第i-1趟不成功比较了i-1次，第i趟成功比较了m次
• 最坏情况：不成功的匹配都发生在串T的最后一个字符。
  ${\sum }_{i=1}^{n-m+1}{P}_i(i\ast m)$=$\frac{m(n-m+2)}{2}$=O(n*m)
  在i-1趟不成功的匹配中比较了(i-1)×m次，第i趟成功的匹配共比较了m次，所以总共比较了i×m次。

KMP算法

对BF算法改进，主串不进行回溯，T向右滑动到新比较起点k。
k怎么找？举个例子：假设主串当前位置为i，子串为j。
S：a b a b c a b c a c b a b
T：a b a b b
T的最后一个b与S中的c不匹配，此时i=4,j=4，T需要向右滑动到比较的新起点。发现k与T串有关。从T中不匹配的位置向前看，abab，很容易看出把T移动到第二个a的位置下，即：
S：a b a b c a b c a c b a b
T：_ _ a b a b b (努力对齐)
找规律：abab,标个序号(0)(1)(2)(3)，发现(0)!=(3)即a!=b，(0)(1)=(2)(3)即ab=ab，(0)(1)(2)!=(1)(2)(3)即aba!=bab，所以有两个元素可以不用重新匹配了，又因为j的下标从0开始，所以k=2，j改成k也就是T的第3个字母与S的i位置的字母比较。
用next[j]表示这个k如下：

next[j]表征着模式T中最大相同前缀子串和左子串（真子串）的长度。

void Next_(char t[],int next[])
{
    int j=1,k;
    next[0]=-1;
    while(t[j]!='\0')
    {
        k=next[j-1];
        while(k!=-1&&t[k]!=t[j-1])//这里的循环怎么理解，看下图
            k=next[k];
        next[j]=++k;
        j++;
    }
}
void KMP(char *s,char *p,int *next)
{
    int i=0,j=0,k;
    while(s[i]!='\0'&&t[i]!='\0')
    {
        if(j==-1||s[i]==t[j])
        {
            i++;
            j++;
        }
        else j=next[j];
    }
    if(t[j]=='\0')
        return i-j;
    else return 0;
}

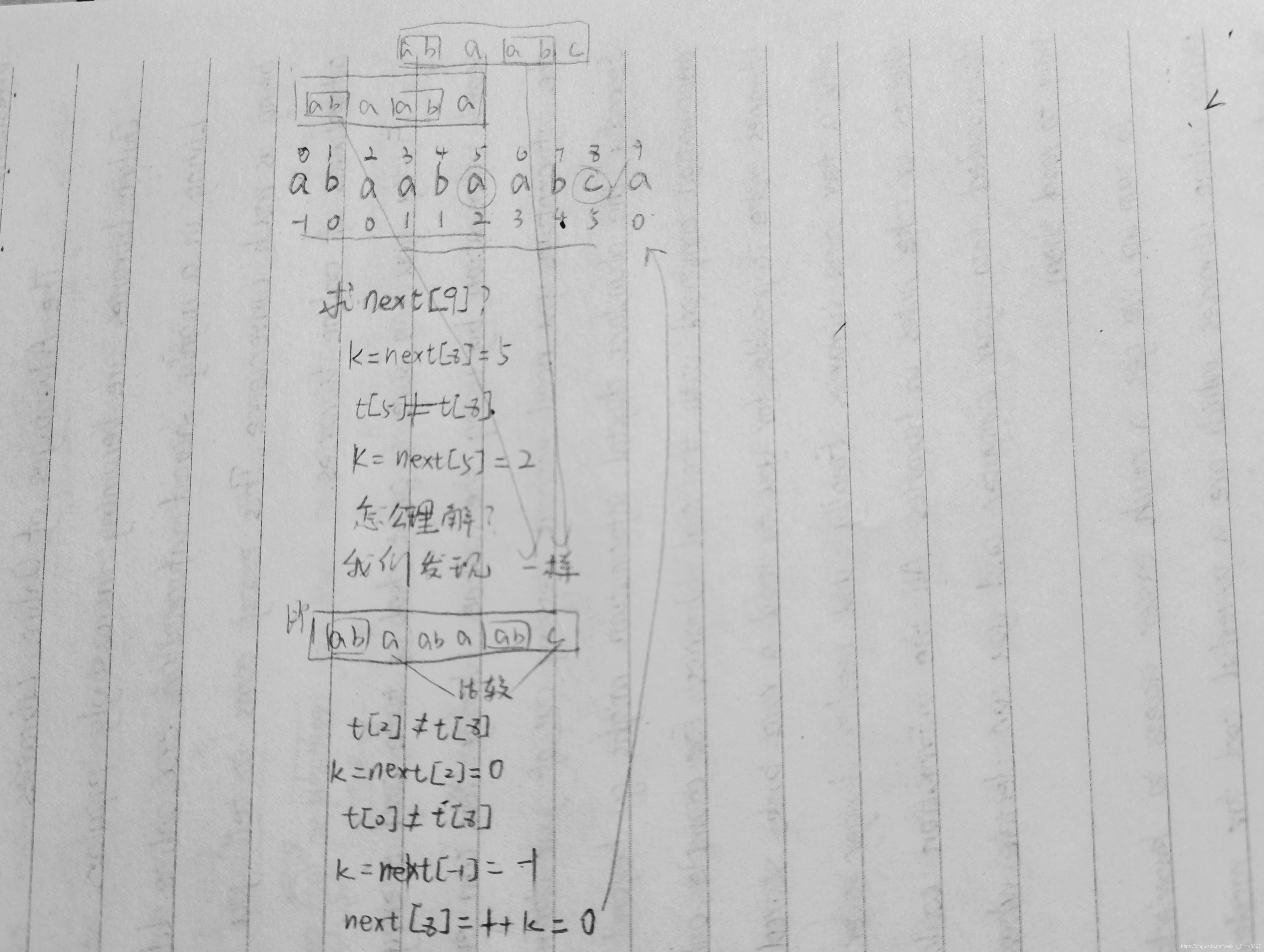
如果t[k] = = t[j-1]或 k = = -1（不存在长度相同的前缀子串和左子串 ）
则t₀t₁…t_k-1t_k= t_j-k…t_j-3t_j-2t_j-1，因此next[j]=k+1，next[j]计算结束
否则， 查找t₀t₁…t_k的最长左子串k=next[k]，转 1 继续执行
最后放个例子：

时间复杂性：O(n+m)

多维数组

一、矩阵的压缩存储

对称矩阵的压缩存储

对于下三角：

• 矩阵行列标从1开始：
  aij在一维数组中的序号= i×(i-1)/2+ j
  ∵一维数组下标从0开始
  ∴aij在一维数组中的下标：k= i×(i-1)/2+ j-1
• 矩阵行列标从0开始：
  aij在一维数组中的序号= i×(i+1)/2+ j+1
  ∵一维数组下标从0开始
  ∴aij在一维数组中的下标：k= i×(i+1)/2+ j

三角矩阵的压缩存储

上三角矩阵的压缩存储：

对角矩阵的压缩存储

二、稀疏矩阵的压缩存储

三元组顺序表

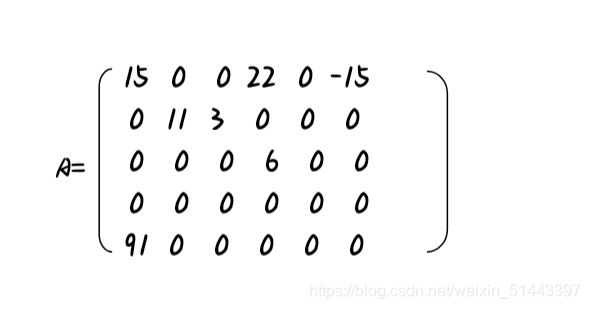
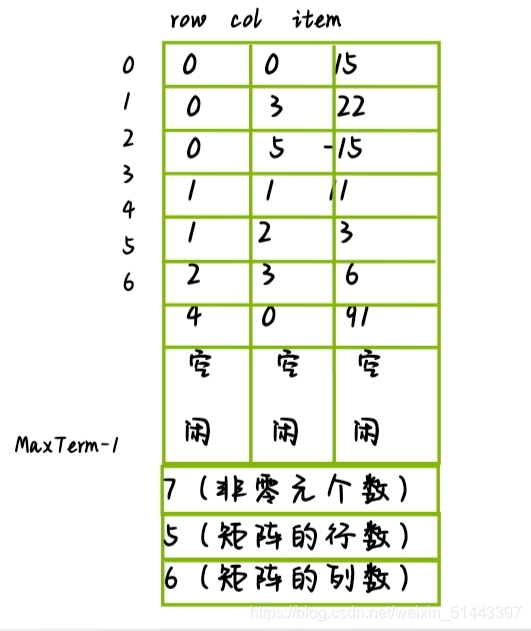
十字链表

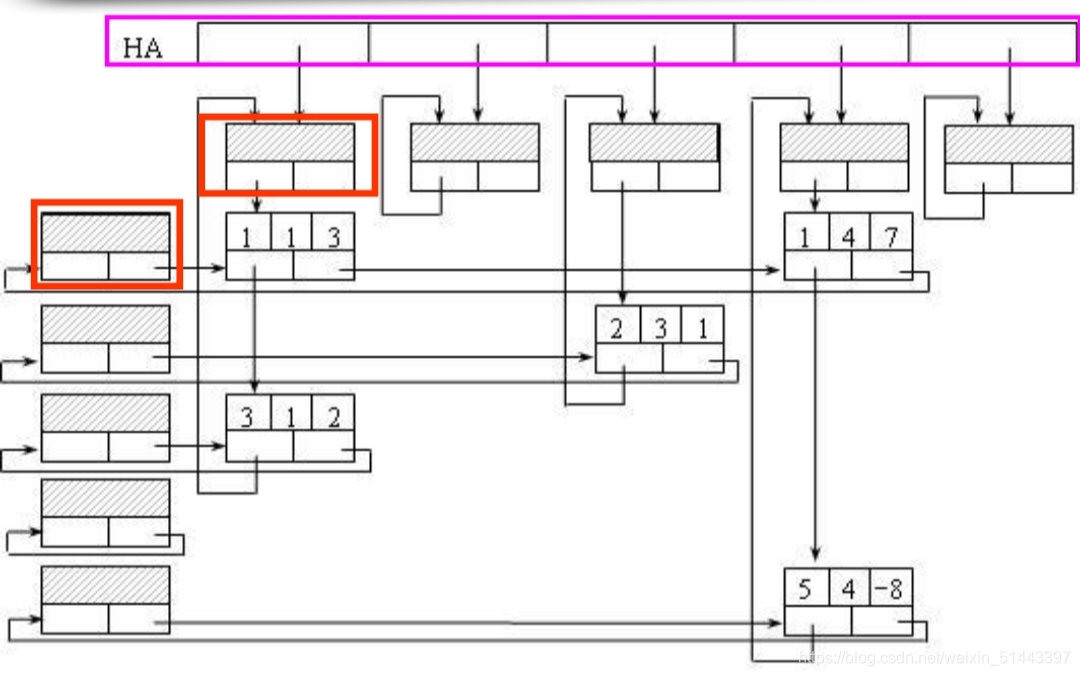
三、二维数组的存储

·两种存储方式：
按行优先：先行后列，先存储行号较小的元素，行号相同者先存储列号较小的元素。
按列优先：先列后行，先存储列号较小的元素，列号相同者先存储行号较小的元素。

按行优先存储的寻址

a_ij前面的元素个数=整行数 * 每个元素个数+ 本行中a_ij前面的元素个数=(i-l₁) * (h₂-l₂+1)+(j-l₂)

列优先存储的寻址

同理；
设数组开始存放位置 LOC( 0, 0 ) = a，每个元素占用 l 个存储单元， 则a[i][j]的存储地址：
LOC ( i, j ) = a + ( j *n +i ) * l

例题：

例：1.将数组称为随机存取结构是因为对数组任一元素的存取时间是相等的
2.数组属于广义线性表，数组被创建以后，其维数和每维中的元素个数是确定的，所以，数组通常没有插入和删除操作
3.从各层元素各自具有的线性关系讲，广义表属于线性结构
4.使用三元组表存储稀疏矩阵的元素，有时并不能节省存储空间，因为三元组表除了存储非零元素值外，还需要存储其行号和列号。
5.稀疏矩阵压缩存储后，必会失去随机存取功能。因为压缩存储后，非零元素的存储位置和行号、列号之间失去了确定的关系
6.线性表可以看成是广义表的特例，如果广义表中的每个元素都是单元素，则广义表便成为线性表。
7.若一个广义表的表头为空表，则此广义表亦为空表。
【解答】错。如广义表 L=(( )，(a，b))的表头为空表，但 L 不是空表。