文章目录
一: 线段树算法分析
1. 基本分析
a.线段树——处理区间查询 / 维护 / 状态更新问题
例如下图:
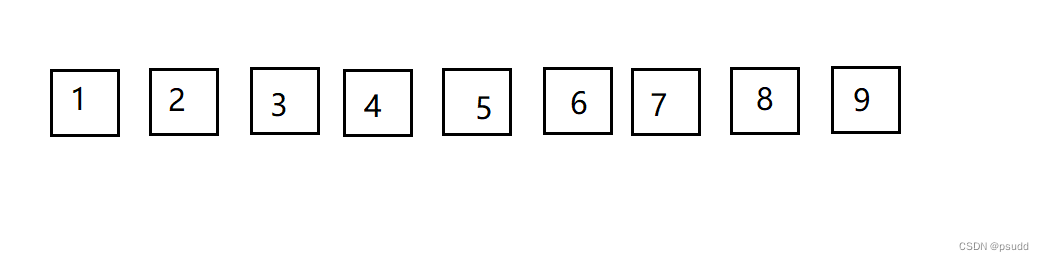
假如我们提出多次的区间修改和查询要求,如果修改是找到指定位置的小方块例如( 4-6方块 + 2 操作),查询也是查询一个区间的和这个样子的操作,如果我们直接对指定区间去逐个修改查询的话这样子的时间复杂度毫无疑问是非常大的。
例如下图:

所以:我们选择一个高效的算法—线段树,去动态储存一段区间的信息,当我们需要再次查找修改信息的时候我们就可以不需要每次再对底层的单个区间进行修改。
这样子当我们再去需要查询 4 - 6 方块的信息的时候起始我们只要按顺序从上到下处理,查询 4 - 5的时候并不需要走到底层查询, 而可以直接查询4 - 5方块信息就可以了。
2. lazy标记
2.1 lazy标记——帮助优化区间的修改
现在重要的问题就在于我们应该什么时候可以去不走到底层修改,什么时候需要走到底层修改, 例如区间 4 - 6 我们分开走走到 4 - 5是不需要再向下走了, 而走到 6 是必须要继续向下走的去修改单独的 6 模块。
并且关键的是我们修改了 4 - 5 区间模块,是没有修改底层 4 和 5 模块的,假如下次我们需要修改 4 模块,我们也是必须走到底层 4 模块 并且需要把上一次对 4 模块的修改一起带到 4 模块去。
例如 :
第一次: 4 - 5 模块 + 2 ,实际 4 模块 = 0.
第二次: 4 模块 + 3 ,实际4模块修改的结果应该是 之前需要修改的+2 和这次需要修改的 +3,所以 实际 4模块 = 5.
2.2 lazy标记——分析和实现
分析过程:
a. 利用lazy[ ]标记我们可以走到这个区间后本来需要向下修改但被我们省略了向下修改的步骤
b. 只有当下次需要继续向下修改的时候我们再一起把lazy[ ]标记下放
实现过程:
a. 什么时候可以省略向下继续修改?
——当我们需要修改的区间[l, r] 可以包括住当前所代表的区区间[st ,ed] 的时候,例如 [l = 4, r = 6 ], [st = 4, ed = 5] 此时我们就可以不需要再继续向下修改了,只要修改这个 4 - 5模块,并将 lazy[ ]标记相应修改,只有当再次需要下放的时候再下放。
if(st >= l && ed <= r ){ // l 和 r 可以完全包裹住这个区间
lazy[node] = solve();
tree[node] = solve();
}
b. 什么时候要将lazy[ ]标记下放
——和省略向下修改步骤原理相反,当你不能再完全将需要修改的模块完全包住的时候就需要下放了,例如你想修改[l = 5, r = 7], [st = 4, ed = 5]这时候你需要修改5但不要修改4,你需要继续向下修改就要先把之前所欠的没有修改的lazy标记进行下放操作
/*
rt : 区间标号 st , ed 此区间包括范围
l, r : 需要修改的区间
k : 需要修改的值
*/
void update(LL rt, LL st, LL ed, LL l, LL r, LL k){
/*
不能完全包裹时 : push_down() 需要下放标记
下放lazy[]标记 ———— 更新下面区间 ————利用已更新好小区间更新这个区间
*/
push_down(rt, st, ed);
LL mid = (st + ed) >> 1;
if(l <= mid) update1(lrt, st, mid, l, r, k);
if(r > mid ) update1(rrt, mid + 1, ed, l, r, k);
push_up(rt, st, ed);
}
3. 动态灵活增加更多标记
a. 为什么需要其他标记?
——很简单因为题目需要,当我们不再是对一个模块单纯求和而需要求其最大值,最小值,等等其他限定条件的时候,我们可以同时在一个模块当中塞入其他标记帮助我们更好解题
例如下图:

二: 线段树基本代码
// rt, st, ed : 区间号码 + 区间左边界 + 区间右边界
// l, r : 需要查询的左右区间
// lrt = rt >> 1, rrt = rt >> 1 | 1
1. 标记下放 + 向上修改区间信息代码
下放标记 —— 需要清空lazy[ ]标记
void push_down(int rt, int st, int ed ){
if(lazy[rt]){
int mid = (st + ed) >> 1;
tree[lrt] += (mid - st +1) * lazy[rt];
lazy[lrt] += lazy[rt];
tree[rrt] += (ed - mid) * lazy[rt];
lazy[rrt] += lazy[rt];
lazy[rt] = 0;
}
}
向上整合区间信息
void push_up(int rt, int st, int ed ){
tree[rt] = tree[lrt] + tree[rrt];
}
2. 建树代码
先建立子树 —— 利用子树信息更新父树
//数组地址,建树的地址,树的起始结点,数的起始和结束位置.
void build_tree(int arr[], int tree[], int rt, int st, int ed){
if(sta == end){
tree[rt] = arr[sta];
return;
}
int mid = (st + ed) >> 1;
build_tree(arr, tree, lrt, st, mid);
build_tree(arr, tree, rrt, mid+1, ed);
push_up(rt, st, ed);
}
3. 区间修改代码
区间修改2个步骤
a. 可以直接修改大区间 —— 修改区间
b. 需要继续向下修改 —— 下放标记 + 修改子区间 + 信息整合
void update(int rt, int st,int ed, int l, int r, int k){ // k是需要操作的大小
if(st >= l && ed <= r){
tree[rt] += (ed - st +1) * k;
lazy[rt] += k;
mx[rt] += k ,mn[rt] += k;
return ;
}
push_down(rt, st, ed);
LL mid = (st + ed) >> 1;
if(l <= mid) update(lrt, st, mid, l, r, k);
if(r > mid ) update(rrt, mid + 1, ed, l, r, k);
push_up(rt, st, ed);
}
4. 区间查询代码
区间查询2个步骤
a. 可以直接查询大区间 —— 返回区间结果
b. 需要继续向下查询 —— 下放标记 + 查询子区间 + 信息整合
int query(int rt, int st, int ed, int l, int r){
if(st >= l && ed <= r) return tree[rt];
push_down(rt, st, ed);
LL mid = (st + ed) >> 1;
LL sum = 0;
if(l <= mid)sum += query(lrt, st, mid, l, r);
if(r > mid)sum += query(rrt, mid+1, ed, l, r);
return sum;
}
三: 例题 分析+细节+代码
a. 例题
2022年江西省大学生程序设计竞赛K题

b. 分析
此题涉及一些限制条件,数最小不能小于0,所以我们可以设置一些额外标记mn[ ], mx[ ]等,正常数值加直接update,数值如果为负则需要利用mx[ ],mn[ ]等进行判断能否对这个区间进行一个区间的操作等,并且设置额外cl[ ]标记看是否需要将下面区间进行清空等等。
c. 细节注意
查询和修改操作:两个大步骤分类
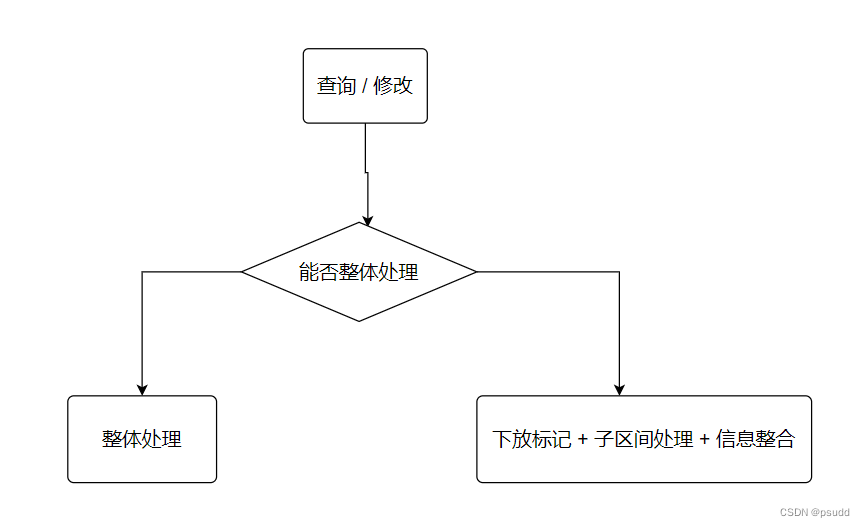
lazy标记,cl标记 :都是判断是否需要对子区间进行处理,本身这个区间已经处理好了
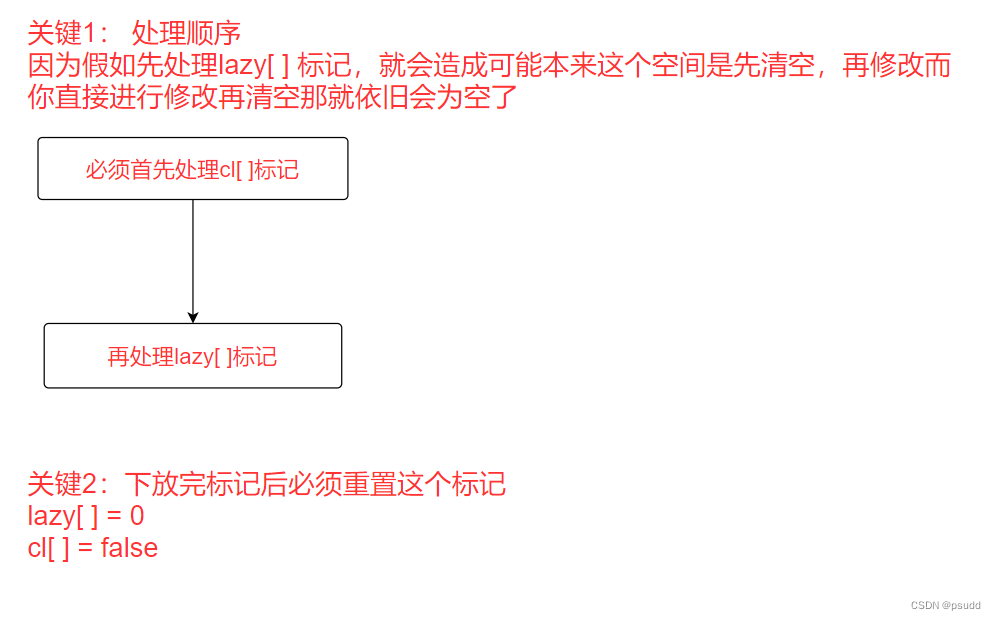
d. 完整代码
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<map>
#define lrt rt << 1
#define rrt rt << 1 | 1
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL tree[N << 2], lazy[N << 2], mx[N << 2], mn[N << 2], n, q;
bool cl[N << 2];
void push_down(LL rt, LL st, LL ed ){
if(cl[rt]){
tree[lrt] = lazy[lrt] = mx[lrt] = mn[lrt] = 0;
tree[rrt] = lazy[rrt] = mx[rrt] = mn[rrt] = 0;
cl[lrt] = cl[rrt] = true ;
cl[rt] = false;
}
if(lazy[rt]){
LL mid = (st + ed) >> 1;
tree[lrt] += (mid - st +1) * lazy[rt];
lazy[lrt] += lazy[rt];
mx[lrt] += lazy[rt], mn[lrt] += lazy[rt];
tree[rrt] += (ed - mid) * lazy[rt];
lazy[rrt] += lazy[rt];
mx[rrt] += lazy[rt], mn[rrt] += lazy[rt];
lazy[rt] = 0;
}
}
void push_up(LL rt, LL st, LL ed ){
tree[rt] = tree[lrt] + tree[rrt];
mx[rt] = max(mx[lrt], mx[rrt] );
mn[rt] = min(mn[lrt], mn[rrt] );
}
LL query(LL rt, LL st, LL ed, LL l, LL r){
if(st >= l && ed <= r) return tree[rt];
push_down(rt, st, ed);
LL mid = (st + ed) >> 1;
LL sum = 0;
if(l <= mid)sum += query(lrt, st, mid, l, r);
if(r > mid)sum += query(rrt, mid+1, ed, l, r);
return sum;
}
void update1(LL rt, LL st, LL ed, LL l, LL r, LL k){ // 更新正值
if(st >= l && ed <= r){
tree[rt] += (ed - st +1) * k;
lazy[rt] += k;
mx[rt] += k ,mn[rt] += k;
return ;
}
push_down(rt, st, ed);
LL mid = (st + ed) >> 1;
if(l <= mid) update1(lrt, st, mid, l, r, k);
if(r > mid ) update1(rrt, mid + 1, ed, l, r, k);
push_up(rt, st, ed);
}
void update2(LL rt, LL st, LL ed, LL l, LL r, LL k){
if(st == ed){
tree[rt] = max( (LL)0, tree[rt] - k );
mn[rt] = mx[rt] = tree[rt];
return ;
}
if(st >= l && ed <= r){
if(k >= mx[rt]){
tree[rt] = lazy[rt] = mn[rt] = mx[rt] = 0;
cl[rt] = true;
return ;
}
else if(k <= mn[rt]){
tree[rt] -= (ed - st +1) * k;
lazy[rt] -= k;
mn[rt] -= k, mx[rt] -= k;
return ;
}
}
push_down(rt, st, ed);
LL mid = (st + ed) >> 1;
if(l <= mid) update2(lrt, st, mid, l, r, k);
if(r > mid ) update2(rrt, mid + 1, ed, l, r, k);
push_up(rt, st, ed);
}
int main(){
ios::sync_with_stdio(false); cin.tie(0);
cin >> n >> q;
while(q -- ){
LL m, a, b, res=0;
cin >> m >> a >> b;
if(m == 0){
LL res = query(1, 1, n, a, b);
cout << res << endl;
}
else if(m > 0){
update1(1, 1, n, a, b, m);
}
else{
update2(1, 1, n, a, b, -m);
}
}
}























 1947
1947











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










