蓝桥杯备赛之动态规划篇——背包问题

💎蓝桥杯系列文章

2023第十四届蓝桥杯模拟赛第二期个人题解（Java实现）
2023第十四届蓝桥杯模拟赛第三期个人题解（Java实现）

蓝桥杯真题——单词分析（Java实现）

💎前言

😘😘哈喽，大家好！这里是蓝桥杯系列文章的动态规划章节🔥🔥，今天要讲解的是动态规划的经典问题——背包问题🍄包括01背包和完全背包。

🙊🙊如果我写的内容有误，欢迎大家在评论区指正👏希望这篇文章对你有帮助❤❤同时欢迎关注我呦👇👇

💎闫氏DP分析法

   前段时间在B站刷到了一个up主——大雪菜自创的动态规划分析方法🔥闫氏DP分析法🔥，个人觉得很不错👍👍后来才知道这个大佬y总就是AcWing的创始人😍y总牛逼！！！
   有时间的小伙伴推荐去看视频👇，讲解会更详细！
  【闫氏DP分析法，从此再也不怕DP问题！】

核心思想
  将问题的所有解看成一个集合，将动态规划问题抽象成集合的划分问题！
核心方法
  从两个角度思考问题：状态表示和状态计算
状态表示(化零为整)
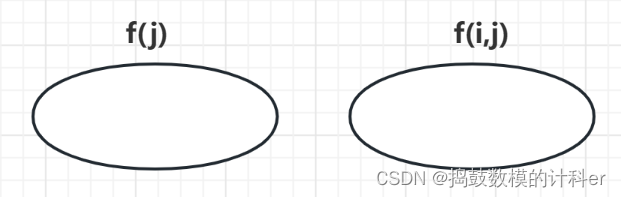
  即问题具体是几维的，一维可以用f(j)表示，二维用f(i,j)表示，从以下两个角度思考：
  问题所代表的集合是什么？即所有满足某个条件下所有解的集合。

  集合的属性是什么？一般是最大值、最小值或数量。一般情况下，问题问的是什么，属性就是什么。
状态计算(化整为零)
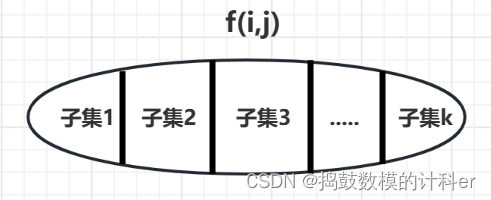
  即集合是如何划分的？
  要求：不重不漏，即一个解应该属于一个集合（如果是最大最小值问题可以忽略）,并且不能有遗漏的解。
  划分依据：找到最后一个不同点。

💎背包问题

🎯0-1背包

问题描述
　　有 N件物品和一个容量是 V 的背包。每件物品只能使用一次。第 i 件物品的体积是 vi，价值是 wi。
　　求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。
输入格式
　　第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。
　　接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。
输出格式
　　输出一个整数，表示最大价值。
样例输入
　　4 5
　　1 2
　　2 4
　　3 4
　　4 5
样例输出
　　8
评测用例规模与约定
　　0<N,V≤1000
　　0<vi,wi≤1000

🌞问题分析

📢📢 这道题用闫氏DP分析法该如何思考呢？
🐾🐾 状态表示：
  0-1背包问题可以看做一个二维的问题，用f(i,j)表示
  集合定义： 所有只考虑前 i 个物品，且总体积不超过j时方案的集合。
  集合属性： 每个方案的最大价值
🐾🐾 状态计算：
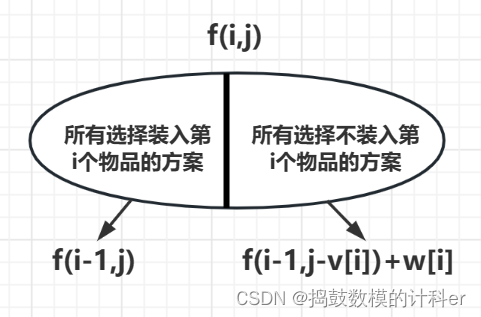
  集合划分： 寻找最后一个不同点，即考虑第 i 个物品时做的决策不同：装入第 i 个物品、不装入第 i 个物品。
  对于所有选择装入第 i 个物品的方案：背包所装物品总价值等于前i-1个所装物品的总价值+第 i 个物品的价值，即
  $f(i-1,j-v[i])+w[i]$
  对于所有选择不装入第 i 个物品的方案：背包所装物品总价值等于前i-1个所装物品的总价值，即
  $f(i-1,j)$
  最大价值只需取两种方案中的最大值:
f ( i , j ) = m a x { f ( i − 1 , j ) , f ( i − 1 , j − v [ i ] ) + w [ i ] } f(i,j) = max\{f(i-1,j),f(i-1,j-v[i])+w[i] \} f(i,j)=max{f(i−1,j),f(i−1,j−v[i])+w[i]}

最后f(N,V)即装入N个物品时背包的最大价值。

💡 Java代码

🍓朴素写法🍓

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
			Scanner sc=new Scanner(System.in);
			int N=sc.nextInt();	//物品数量
			int V=sc.nextInt();	//背包容量
			int[] v=new int[N+1];	//物品重量
			int[] w=new int[N+1];	//物品价值
			for(int i=1;i<=N;i++) {
				v[i]=sc.nextInt();	
				w[i]=sc.nextInt();
			}
			int[][] dp=new int[N+1][V+1];//装入i个物品，且容量不超过V时背包的最大价值
			for(int i=1;i<=N;i++)	//遍历每一个物品
				for(int j=0;j<=V;j++) {	//遍历每一个容量
					dp[i][j]=dp[i-1][j];
					if(j>=v[i])
						dp[i][j]=Math.max(dp[i][j], dp[i-1][j-v[i]]+w[i]);
				}
			System.out.println(dp[N][V]);
		}
}

🍒改进写法🍒
  只需用到一维数组，将背包容量从大到小遍历即可：
$dp[i][j]=Math.max(dp[i][j],dp[i-1][j-v[i]]+w[i])$
  当$j$ 从小到大遍历，$j-v[i]$比$j$先算出来，因此到第i层时，$j-v[i]$就是第i层算出来的$j-v[i]$,而式子中的$j-v[i]$是$i-1$层的，因此不可以；
  反之，若$j$ 从大到小遍历，到第i-1层时，$j-v[i]$算出来恰好就是i-1层的$j-v[i]$，说明 j 应该从大到小遍历。

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
			Scanner sc=new Scanner(System.in);
			int N=sc.nextInt();	//物品数量
			int V=sc.nextInt();	//背包容量
			int[] v=new int[N+1];	//物品重量
			int[] w=new int[N+1];	//物品价值
			for(int i=1;i<=N;i++) {
				v[i]=sc.nextInt();	
				w[i]=sc.nextInt();
			}
			int[] dp=new int[V+1];//装入i个物品，且容量不超过V时背包的最大价值
			for(int i=1;i<=N;i++)//遍历每一个物品
				for(int j=V;j>=v[i];j--) {//遍历每一个容量，从大到小遍历
					dp[j]=Math.max(dp[j], dp[j-v[i]]+w[i]);
				}
			System.out.println(dp[V]);
		}
}

🎯完全背包

问题描述
　　有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。第 i 种物品的体积是 vi ，价值是 wi 。
　　求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。
输入格式
　　第一行两个整数，N，V ，用空格隔开，分别表示物品种数和背包容积。
　　接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 种物品的体积和价值。
输出格式
　　输出一个整数，表示最大价值。
样例输入
　　4 5
　　1 2
　　2 4
　　3 4
　　4 5
样例输出
　　10
评测用例规模与约定
　　0<N,V≤1000
　　0<vi,wi≤1000

🌞问题分析

📢📢 完全背包问题与01背包的区别就在于：完全背包的每种物品可以无限次使用，而01背包每种物品只能使用一次。接下来还是用闫氏DP分析法：
🐾🐾 状态表示：
  完全背包问题可以看做一个二维的问题，用f(i,j)表示
  集合定义： 所有只考虑前 i 个物品，且总体积不超过j时方案的集合。
  集合属性： 每个方案的最大价值
🐾🐾 状态计算：
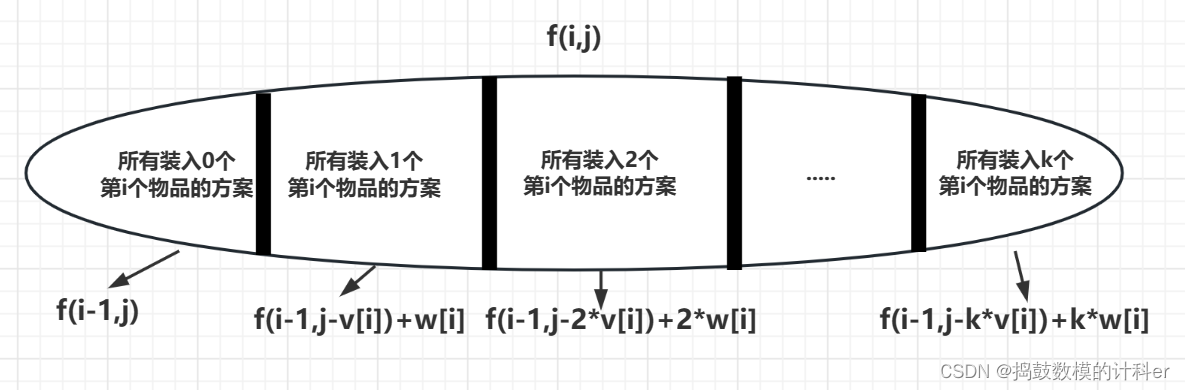
  集合划分： 寻找最后一个不同点，即考虑第 i 个物品时做的决策不同：装入 k 个第 i 个物品 （k≥0）
  对于所有选择装入 k 个第 i 个物品的方案：背包所装物品总价值等于前i-1个所装物品的总价值+ k个第 i 个物品的价值，即 $f\left(i-1,j-k\times v[i]\right)+k\times w[i]$

最大价值只需取所有方案中的最大值:
f ( i , j ) = max ⁡ { f ( i − 1 , j ) , f ( i − 1 , j − v [ i ] ) + w [ i ] , … , f ( i − 1 , j − k × v [ i ] ) + k × w [ i ] } f(i,j)=\max \{f(i-1, j), f(i-1, j-v[i])+w[i], \ldots, f(i-1, j-k \times v[i])+k \times w[i]\} f(i,j)=max{f(i−1,j),f(i−1,j−v[i])+w[i],…,f(i−1,j−k×v[i])+k×w[i]}
上面这个式子可不可以化简呢？

不妨将j替换成i-v[i]试试：
f ( i , j − v [ i ] ) = max ⁡ { f ( i − 1 , j − v [ i ] ) + w [ i ] , f ( i − 1 , j − 2 × v [ i ] ) + 2 × w [ i ] , … , f ( i − 1 , j − k × v [ i ] ) + k × w [ i ] } f(i,j-v[i])=\max \{f(i-1, j-v[i])+w[i], f(i-1, j-2\times v[i])+2\times w[i], \ldots, f(i-1, j-k \times v[i])+k \times w[i]\} f(i,j−v[i])=max{f(i−1,j−v[i])+w[i],f(i−1,j−2×v[i])+2×w[i],…,f(i−1,j−k×v[i])+k×w[i]}
然后上式–下式，得
f ( i , j ) = max ⁡ { f ( i − 1 , j ) , f ( i , j − v [ i ] ) } f(i,j)=\max\{f(i-1,j),f(i,j-v[i])\} f(i,j)=max{f(i−1,j),f(i,j−v[i])}

最后f(N,V)即装入N个物品时背包的最大价值。

💡 Java代码

🍓朴素写法🍓

import java.util.Scanner;

public class Main {
		//朴素写法
		public static void main(String[] args) {
			Scanner sc=new Scanner(System.in);
			int N=sc.nextInt();	//物品数量
			int V=sc.nextInt();	//背包容量
			int[] v=new int[N+1];	//物品重量
			int[] w=new int[N+1];	//物品价值
			for(int i=1;i<=N;i++) {
				v[i]=sc.nextInt();	
				w[i]=sc.nextInt();
			}
			int[][] dp=new int[N+1][V+1];//装入i个物品，且容量不超过V时背包的最大价值
			for(int i=1;i<=N;i++)
				for(int j=0;j<=V;j++) {
					dp[i][j]=dp[i-1][j];
					if(j>=v[i])
						dp[i][j]=Math.max(dp[i][j], dp[i][j-v[i]]+w[i]);
				}
			System.out.println(dp[N][V]);
		}
}

🍒改进写法🍒
  和01背包的改进方法类似，只需用到一维数组，但是要将背包容量从小到大遍历：
$dp[i][j]=Math.max(dp[i][j],dp[i][j-v[i]]+w[i])$
  当$j$ 从小到大遍历，$j-v[i]$比$j$先算出来，因此到第i层时，$j-v[i]$就是第i层算出来的$j-v[i]$；
  反之，若$j$ 从大到小遍历，到第i层时，$j-v[i]$还没算出来，此时的$j-v[i]$就是$i-1$层的,就会得到错误的结果,(其实就是01背包的结果）

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner sc=new Scanner(System.in);
		int N=sc.nextInt();	//物品数量
		int V=sc.nextInt();	//背包容量
		int[] v=new int[N+1];	//物品重量
		int[] w=new int[N+1];	//物品价值
		for(int i=1;i<=N;i++) {
			v[i]=sc.nextInt();	
			w[i]=sc.nextInt();
		}
		int[] dp=new int[V+1];//装入i个物品，且容量不超过V时背包的最大价值
		for(int i=1;i<=N;i++)
			for(int j=v[i];j<=V;j++) {
				dp[j]=Math.max(dp[j], dp[j-v[i]]+w[i]);
			}
		System.out.println(dp[V]);

	}
}

💎总结

💥💥看到这里，你搞清楚01背包和完全背包的的差别了吗？

🔥🔥如果你觉得这篇文章对你有帮助，欢迎点赞评论收藏，或者关注我呦！！！爱你们😘