2021 ICPC区域赛（上海）H-Life is a Game（kruskal重构树、LCA）(Hack数据 + 真正解)

游戏人生

题目大意

• 给你一个图，图上有点权和边权。以及q个查询：每个查询给你一个初始位置x和初始能量k；
• 你每到一个新点上即可获得该点的能量（即点权），但是如果想通过一条边，你的能量总数需要大于边权（可以来回走）
• 求可以获取的最大能量数。

引用 lwz_159的题解博客

首先贪心地想，能走到最多的点肯定能获得更多能量，但边权会是限制，在可以来回走的前提下，我们显然可以保留限制最小的边让这个图变成一颗树（最小生成树）

但仅仅有 最小生成树 并不能很好地处理 q 次询问的时间复杂度，这里我们再次引入 Kruskal重构树 来解决

什么是kruskal重构树？

类型题：洛谷：P2245 星际导航

在一颗 kruskal重构树 上，我们拥有神奇的性质：

• 这颗树上叶子节点都代表原图中的点，其余结点都是代表原图中的边
• 任意原最小生成树中的两点之间路径上 最大 的边权是他们在重构树上 最近公共祖先 lca 这个点的权值（这个点必定代表边）
• 这颗树有权值的点都代表边，他们会构成一个二叉堆，即一个子树的根节点权值必定大于他内部所有结点的权值（这里的权值是针对边的）

拥有了这样一颗重构树，我们就能用倍增的方式每次处理查询

每次询问我们都会得到一个起始点（根据原则必定是叶子节点）和起始值，假设为图中的 a 点；在这颗重构树上我们每次尽可能往根节点跳，判断能不能跳过去就是判断 a点的值 是否大于等于 b点的值（边权限制）

一旦我们能跳到 b点，因为二叉堆的性质 b这条边 会是 b这个子树中最大的一条边，所以我们必定能得到 b子树中所有点的权值（最大的边都能走，其他小边肯定也能走过去）（这里的权值针对点）

跳的过程用倍增压缩，这样总时间就可以在 $O(qlogn)$ 内，一旦某次怎么都跳不上去我们就可以退出了（止步于此）

$Code:$

#include<bits/stdc++.h>
#include<unordered_map>
#define mem(a,b) memset(a,b,sizeof a)
#define cinios (ios::sync_with_stdio(false),cin.tie(0),cout.tie(0))
#define sca scanf
#define pri printf
#define forr(a,b,c) for(int a=b;a<=c;a++)
#define rfor(a,b,c) for(int a=b;a>=c;a--)
#define endl "\n"
//[博客地址]：https://blog.csdn.net/weixin_51797626?t=1
using namespace std;
inline void read(int& x) { x = 0; int f = 1; char ch = getchar(); while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); } while (ch >= '0' && ch <= '9') { x = x * 10 + (ch - '0'); ch = getchar(); } x *= f; }
void write(int x) { if (x < 0) putchar('-'), x = -x; if (x >= 10) write(x / 10); putchar(x % 10 + '0'); }

typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;

const int N = 200010, M = 100010, MM = N;
int INF = 0x3f3f3f3f, mod = 1e9 + 7;
ll LNF = 0x3f3f3f3f3f3f3f3f;
int n, m, k, T, S, D;
struct edge
{
	int a, b, w;
	bool operator <(const edge& ee)const { return w < ee.w; }
}ed[M];
vector<int> e[N];//重构树，重构树最多会比原最小生成树多一倍的点
int a[N], p[N], down[N];
ll d[N];
int fa[N][18];

int find(int x) {
	return p[x] == x ? p[x] : p[x] = find(p[x]);
}

int kruskal() { //先创建最小生成树
	sort(ed + 1, ed + 1 + m);
	forr(i, 1, 2 * n)p[i] = i;
	int cnt = n;
	forr(i, 1, m) {
		int a = find(ed[i].a), b = find(ed[i].b);
		if (a ^ b) {
			d[++cnt] = ed[i].w;//同时用并查集建重构树
			p[a] = p[b] = cnt;
			e[cnt].push_back(a);
			e[cnt].push_back(b);
		}
	}
	return cnt;
}

int build(int x) { //递归预处理倍增，队列也可，不容易爆栈
	int sum = a[x];
	for (auto j : e[x]) {
		fa[j][0] = x;
		for (int i = 1; i <= 17; i++)
			fa[j][i] = fa[fa[j][i - 1]][i - 1];
		sum += build(j);
	}
	down[x] = sum;//以及以某点为根的子树内所有点权和
	return sum;
}

int main() {
	cinios;

	cin >> n >> m >> k;
	forr(i, 1, n)cin >> a[i];

	forr(i, 1, m) {
		int a, b, x;
		cin >> a >> b >> x;
		ed[i] = { a,b,x };
	}

	n = kruskal();
	build(n);
	d[0] = 1e18;//边界要给个极值

	forr(i, 1, k) {
		int x, q;
		cin >> x >> q;

		ll ans = 1ll * a[x] + q;
		while (x != n)//跳到根节点为止
		{
			int x1 = x;
			for (int i = 17; i >= 0; i--)
				if (d[fa[x][i]] <= ans) {
					x = fa[x][i];//能跳我们就跳上去
					ans = 1ll * down[x] + q;
					//随时更新携带的能量
				}
			if (x == x1)break;//如果某轮怎么都跳不动就退出
		}
		cout << ans << '\n';
	}

	return 0;
}
/*
*/

Hack数据 + 真正解

• 感谢 @weixin_49667031 的评论，上面的代码实际上是能被以下极端数据卡掉的：

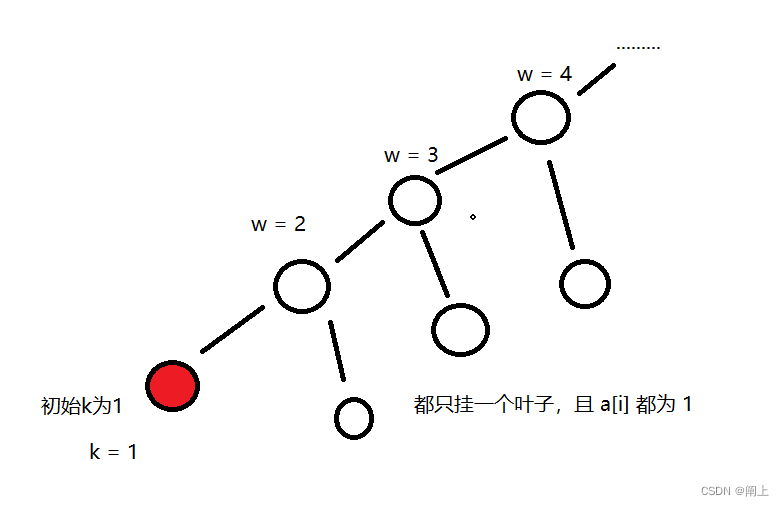
如果是上面的代码，在这一段

		ll ans = 1ll * a[x] + q;
		while (x != n)//跳到根节点为止
		{
			int x1 = x;
			for (int i = 17; i >= 0; i--)
				if (d[fa[x][i]] <= ans) {
					x = fa[x][i];//能跳我们就跳上去
					ans = 1ll * down[x] + q;
					//随时更新携带的能量
				}
			if (x == x1)break;//如果某轮怎么都跳不动就退出
		}
		cout << ans << '\n';

枚举向上跳跃的 $2^i$ 步数时，因为 ans 需要随时更新，我们最坏情况只能跳一步更新一下，用更新后变大的 ans 促使你之后继续上跳

在极端数据的情况下，叶子只有 n/2 个，则跳跃长度，枚举的次数也需要 n/2，此算法就退化成 $O(n^2)$ 了。

但这个数据是能过牛客的，可能是出题人只想考察 重构树算法，保证了数据随机。

• 那么我们要如何解决呢？显然 ans 是关键，正是因为它的不固定性退化了算法。

对于每个点，我们假设能跳到该点，自然能获得以该点为根的子树内所有的 $\sum a[i]$ ，如果想要突破到这个点的父亲，则需要一个最低初始能量：$need[i]=w[fa[i]]-\sum a[i]$。

每个点都维护一个从自身出发，往上跳 $2^j$ 步的路径中，所需要的 最大 最低初始能量，显然如果初始给的 K 能量能 大于等于 这个 最大 最低初始能量，就能跳到 $fa[i][j]$ 点。

预处理完这些，我们跳跃的时候就能摆脱 ans 的不固定性，让每次比较都与 固定的 初始能量 K 有关，这样算法的复杂度就真真正正做到了 $O(qlogn)$，空间比之前大了一倍，但绰绰有余。

上代码：

#include<bits/stdc++.h>
#include<unordered_map>
#define debug cout << "debug---  "
#define debug_ cout << "\n---debug---\n"
#define oper(a) operator<(const a& ee)const
#define forr(a,b,c) for(int a=b;a<=c;a++)
#define mem(a,b) memset(a,b,sizeof a)
#define cinios (ios::sync_with_stdio(false),cin.tie(0),cout.tie(0))
#define all(a) a.begin(),a.end()
#define sz(a) (int)a.size()
#define endl "\n"
#define ul (u << 1)
#define ur (u << 1 | 1)
using namespace std;

typedef unsigned long long ull;
typedef long long ll;
typedef pair<ll, int> PII;

const int N = 2e5 + 10, M = 2e6 + 10, mod = 1e9 + 7;
int INF = 0x3f3f3f3f; ll LNF = 0x3f3f3f3f3f3f3f3f;
int n, m, B = 10, ki;

struct edge
{
    int a, b, w;
    bool oper(edge) { return w < ee.w; }
}ed[M];
ll w[N], a[N];
int p[N];
int find(int x) {
    return p[x] == x ? p[x] : p[x] = find(p[x]);
}

vector<int> e[N];

//重构树
void kruskal() {
    for (int i = 0; i <= 2 * n + 2; i++)p[i] = i;
    sort(ed + 1, ed + 1 + m);
    int cnt = n;
    for (int i = 1; i <= m; i++) {
        auto [a, b, x] = ed[i];
        a = find(a), b = find(b);
        if (a ^ b) {
            w[++cnt] = x;
            p[a] = p[b] = cnt;
            e[cnt].push_back(a);
            e[cnt].push_back(b);
        }
    }
    n = cnt;
}

int fa[N][18];
ll mx[N][18], need[N];

void dfs(int x) {
    for (int to : e[x]) {
        fa[to][0] = x;
        for (int j = 1; j <= 17; j++)
            fa[to][j] = fa[fa[to][j - 1]][j - 1];
        
        dfs(to);

        a[x] += a[to];
    }
    //a 数组存储 若能抵达 x，获取的 x 子树内所有的 a 值（能量）

    need[x] = w[fa[x][0]] - a[x];
    //need 存储，x 点突破到父亲所需的 最少能量
}

//mx 数组维护 从 x 点往上跳 2^j 步的路径内 最大的 need 值
void dfs_up(int x) {
    for (int to : e[x]) {
        mx[to][0] = need[to]; //跳 1 步就是突破 to 本身 到 fa[to]

        //need[to] !!! 不是 need[x]
        for (int j = 1; j <= 17; j++)
            mx[to][j] = max(mx[to][j - 1], mx[fa[to][j - 1]][j - 1]);
        dfs_up(to);
    }
}

void solve() {
    int q;
    cin >> n >> m >> q;

    for (int i = 1; i <= n; i++)cin >> a[i];

    for (int i = 1; i <= m; i++) {
        auto& [a, b, w] = ed[i];
        cin >> a >> b >> w;
    }
   
    kruskal();

    dfs(n);
    a[0] = a[n];//有可能跳到根节点之上

    dfs_up(n);

    while (q--)
    {
        ll x, k;
        cin >> x >> k;

        //只要该路径满足 mx[x][j] <= k 就跳上去，这样就是稳定的 O(qlogn)
        for (int j = 17; j >= 0; j--)
            if (mx[x][j] <= k)
                x = fa[x][j];

        cout << a[x] + k << endl;
    }
}

signed main() {
    cinios;
    int T = 1;
    for (int t = 1; t <= T; t++) {
        solve();
    }
    return 0;
}
/*
*/
//板子

一年前写这博客时还没想那么多，参考了别人的写法，现在看看还是有蛮多收获(x)错误(√)的