数据结构与算法（空间复杂度）

回顾

O(1)

int i = 8;
int j = 6;
int sum = i + j;

只有代码的执行时间不随n的增大而增长，这样代码的时间复杂度我们都记作O(1)。或者说，一般情况下，只要算法中不存在循环语句、递归语句，即使有成千上万行代码，其时间复杂度也是O(1)。

O(log n)、O(n log n)

i = 1;
while (i <= n) {
	i = i + 2;
}

由于第三行是循环次数最多的，分析上面代码可以看出，变量i的值从1开始取，每循环一次就乘以2.当大于n时，循环结束。显然是个等比数列：

2^0 、 2^1 、 2^2 、 …… 、 2^k 、…… 、 2^x = n

所以，我们只需要知道x值是多少，就知道这行代码执行的次数了。通过2^x = n求解x这个问题。故 x = log 2 ^ (n)，所以这段代码的时间复杂度就是O(log 2 ^ (n))。

分析以下代码的时间复杂度：

i = 1;
while (i <= n) {
	i = i * 3;
}

通过以上的分析显然可以得出时间复杂度是O(log 3 ^ (n))。

综上可得，不管是以2为底还是3为底甚至还是10为底，我们都可以把所有的对数阶的时间复杂度都记为O(log n)。
因为对数之间是可以转换的，log 3 ^ (n) 等于 (log 3 ^ (2))*log 2 ^ (n)，所以O(log 3 ^ (n)) = O(C * log 2 ^ (n))，其中C = log 3 ^ (2) 为常量，忽略常量后就得O(C f(n)) = O(f(n))。所以，O(log 2 ^ (n)) = O(log 3 ^ (n))。因此，我们再忽略“底”，统一可得O(log n)。

O(m+n)、O(m * n)

直接上代码

int cal(int m, int n) {
	int sum_1 = 0;
	int i = 1;
	for(; i < m; ++i) {
		sum_1 = sum_1 + i;
	}
	int sum_2 = 0;
	int j = 1;
	for(; j < n; ++j) {
		sum_2 = sum_2 +j;
	}
	return sum_1 + sum_2;
}

我们可以看出，m和n是两个数据规模，我们无法看出谁的量级最大，因此时间复杂度分析时我们无法再用加法法则。因此，以上代码的时间复杂度为O(m + n)。
所以 加法法则改为： T1(m) + T2(n) = O1(f(m) + g(n))。但是乘法法则依然有效：T1(m) * T2(n) = O(f(m) * f(n))。

空间复杂度

分析以下代码的复杂度

void print(int n) {
	int i = 0;
	int[] a = new int[n];
	for ( i; i < n; ++i) {
		a[i] = i * i;
	}
	for( i = n - 1; i >= 0; --i) {
		print out a[i];
	}
}

跟时间复杂度分析一样，可以看出，第2行代码中，我们申请了一个空间存储变量i，但是常量阶的，与数据规模无关，忽略。第3行代码申请了一个大小为n的int数组 ，因此，整段代码的空间复杂度为O(n)。

我们常见的空间复杂度就是O(1)、O(n)、O(n²)。对数阶的复杂度平时用不到。

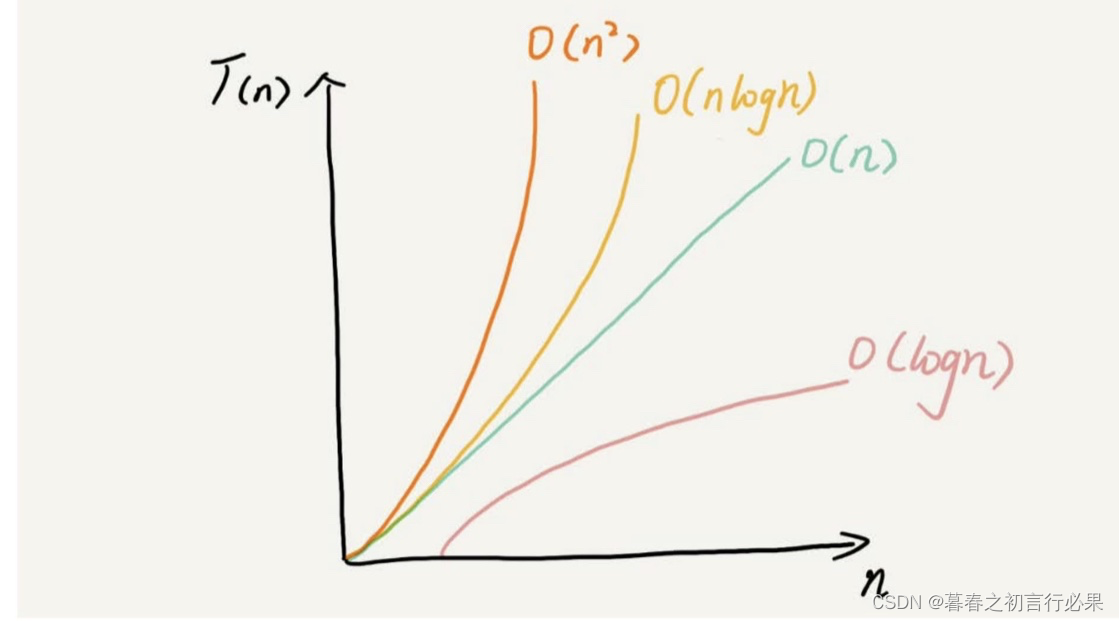
总结，从低阶到高阶依次为：O(1)、O(logn)、O(n)、O(nlogn)、O(n²)。如下图所示：