目录
写在前面
最近开始学C++,看了北大李戈教授的C语言程序设计课程,在学到了新的知识的同时也深深被其清晰的逻辑和通俗易懂的讲解所折服。最近正在看C++的递归调用部分,李老师举了三个比较典型的递归应用题,为了加深对递归的理解以及更加熟练地应用C++,我在此写下这篇文章,自己动手用C++代码将老师课上说的三个例子实现了一遍。
1. 递归的定义
首先,在说递归应用之前,我们先来回顾一下什么是递归。其实递归本身的定义不难理解,就是在定义的函数中直接或间接调用函数本身。
2. 递归的过程
但是对于初学者来说,很可能会对递归的过程感到困惑,递归到底是怎么样一个执行过程呢?下面用一个简单的例子也是李教授上课所讲到的例子来帮助大家理解递归的过程。
#include<iostream>
using namespace std;
int recur(){
char c;
c = cin.get();
if(c!='\n')
recur();
cout<<c;
return 0;
}
int main(){
recur();
return 0;
}
对于上面的代码,我们把abc (注意最后按回车键)作为输入,然后判断输出结果。
首先在main函数中调用recur()方法, abc将会被逐个读入,根据条件语句的判断会一直调用recur()方法,直到遇到最后\n,recur()方法不再被调用,然后继续执行打印\n,所以第一次输出的第一个字符为\n。但是需要注意的是由于输入的abc一直满足条件判断在执行recur()方法的调用,所以返回的值是返回到if条件语句下的recur()中的。由于输入的是abc, 所以recur()方法内部的recur()被调用了3次,所以后面还会再执行三次打印。首先被打印出来的是c,这也很好理解,因为在没遇到换行符之前,会一直读到c,因此先打印出来的就吃c。同理,接着b被打印出来,最后是a。因此输出为 cba。
由递归过程演示我们可以知道,递归其实是反向输出,即自下而上求解的思想。因此这也能解释为什么我们在后面递归问题例子求解第n个情况与(n-1)个情况的关系的时候,我们需要把关注点放在结果上,这样才能使程序按原顺序执行。
3. 递归的应用
说了递归的定义和过程,接下来我们就来举几个例子来说说递归的应用。以下例子都源自于李老师上课所解释的例子并且用C++代码一步步实现。
3.1 用递归解决递推问题
3.1.1 切饼问题
第一个例子是用于解决递推问题的切饼问题,用刀沿直线在饼上切n刀,求出切完后饼的最大块数。
首先我们对问题进行解析,如果想让一刀下去能切出最多的块数,我们首先要确保每新切的一刀都与原来的所有刀有交点,这样就能分出最大块数。因此我们画出了n=1,2,3,4的情况,如下图所示。
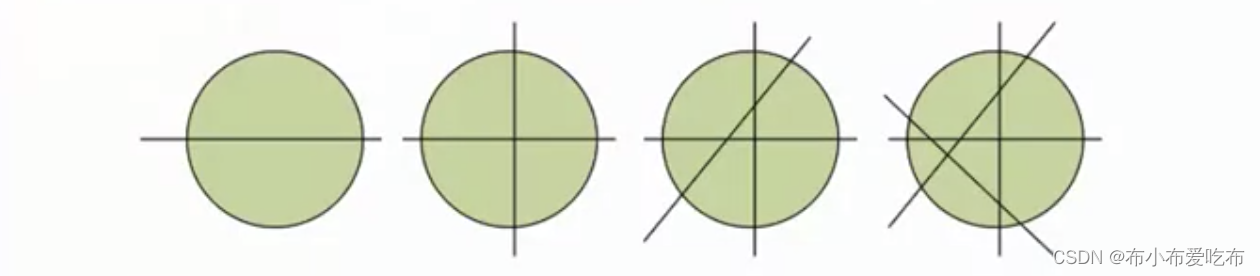
定义q(n)为求切n刀时,能分出饼的最大块数,则:
n = 0, q(0) = 1
n = 1, q(1) = q(0) + 1
n = 2, q(2) = 4 = q(1) + 2
n = 3, q(3) = 7 = q(2) + 3
n = 4, q(4) = 10 = q(3) + 4
...
因此,我们可以由上述关系可得出递推关系式:
q(n) = q(n-1) + n
如果我们不用递归的方法,我们可以写个循环语句求解该问题。这里不再具体展开详述。我们由递推关系得出的关系式可知,如果想要求第n刀能切取的最大块数q(n),我们需要知道第(n-1)刀能切出的最大块数q(n-1)。那第(n-1)刀的最大块数q(n-1)怎么求呢?我们需要知道第(n-2)刀的最大块数q(n-2)。以此向前推,最后我们发现,我们只需要知道第0刀即当n=0时能切出的最大q(0)即可。由前面的分析可知q(0) = 1,因此我们可以根据递推关系式和初始情况可以写出如下程序解决这个问题:
#include<iostream>
using namespace std;
int q(int n){
if(n==0)
return 1;
else
return q(n-1) + n;
}
int main(){
cout<<q(4)<<endl;
return 0;
}
输出的结果如下:
11
3.1.2 斐波那契数列
有如下一组数据,请根据前面的情况求第n个数的值。
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ..., n
定义f(n)为第n个数的值,则
n = 1, f(1) = 1
n = 2, f(2) = 1
n = 3, f(3) = 2 = f(2) + f(1)
n = 4, f(4) = 3 = f(3) + f(2)
n = 5, f(5) = 5 = f(4) + f(3)
n = 6, f(6) = 8 = f(5) + f(4)
n = 7, f(7) = 13 = f(6) + f(5)
...
我们可以由上述关系得出递推关系式:
f(n) = f(n-1) + f(n-2)
由前面的切饼问题分析可得,我们需要知道初始条件n=1和n=2时,f(1)和f(2)的值即可。我们可以根据分析写一段程序解决这个问题:
#include<iostream>
using namespace std;
int f(int n){
if(n==1||n==2)
return 1;
else
return f(n-1) + f(n-2);
}
int main(){
cout<<f(12)<<endl;
return 0;
}
输出的结果如下:
144
3.1.3 递推与递归
由上述的例题我们可以看出,递推由起始条件向后推,即根据 i = 0, 1, 2, ,3... 的情况推测 i = n 的情况。因此递推的关注点在起始条件上。而递归则相反,递归的关注点在目标求解上,更关注于 i = n 时的情况。两者的共同之处在于它们都体现了当前情况与前面的情况之间的关系。
递归程序的优点在可以简化复杂的循环语句程序。
实现递归的解决递推问题的方法很简单,将目标放在目标求解上
- 找到第n次与第n-1次执行的关系
- 确定初始状态时的返回结果
3.2 模拟连续发生的动作
3.2.1 进制转换
来看一个把十进制转二进制的例子:
将123转换为二进制数。
十进制转二进制采用除2取余法,具体计算过程如下:
除以2取商(整数) 余数
123 / 2 = 61 1
61 / 2 = 30 1
30 / 2 = 15 0
15 / 2 = 7 1
7 / 2 = 3 1
3 / 2 = 1 1
1 / 2 = 0 1
又上述过程我们可以看出,商不为0的时候,会一直执行除以2取余的操作。当商为0
的时候,我们会返回被除数的值,然后程序结束。最后自下而上收集余数得到的结果为十进制的二进制表达。
1111011
我们可以将上述问题转化为代码求解,具体实现过程如下:
#include<iostream>
using namespace std;
void deToBi(int n){
//如果商不为0则一直进行除2取余的操作
if(n/2!=0){
deToBi(n/2); // 除2
cout<<n%2; // 取余
}
else{
cout<<n;
}
}
int main(){
deToBi(123);
cout<<endl;
return 0;
}
输出结果如下
1111011
3.2.2 汉诺塔
汉诺塔问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。

我们可以用列举法观察有不同盘子数目的情况:
n = 1
1 1号盘 A -> C
(把1号盘放在C柱上)
n = 2
1 1号盘 A -> B
2 2号盘 A -> C
3 1号盘 B -> C
(把1和2号盘放在C柱上)
n = 3
1 1号盘 A -> C
2 2号盘 A -> B
3 1号盘 C -> B
4 3号盘 A -> C
5 1号盘 B -> A
6 2号盘 B -> C
7 1号盘 A -> C
(先把1和2号盘放在B柱上,3号盘放在C柱上,再把1和2号盘放在C柱上)
从上述分析不难看出,如果是4个盘子,那么就是先把1,2和3号盘子放在B柱子上,把4号盘放在C柱子上,最后再把1,2和3号盘子放在C柱子上。
因此这个问题可以简化为3个步骤:
- 把(n-1)个盘子由A借助C移动到B
- 把第n个盘子由A移动到C
- 把(n-1)个盘子由B借助A移动到C
因此我们如果想实现 move(n, A,B,C), 则需实现:
move(n-1,A,C,B)
move n from A to C
move(n-1,B,A,C)
用代码实现形式如下,这个是基于李老师给的例子进行的改进,打印出了第几次:
#include<iostream>
using namespace std;
int m = 0;
void printMove(int plate, char X, char Y){
cout<<"第"<< (++m) <<"次移动:把"<<plate<<"号圆盘从 " << X << "移到 " << Y<<endl;
}
void move(int n, char A, char B, char C){
if (n==1)
printMove(n,A,C);
else{
move(n-1,A,C,B);
printMove(n,A,C);
move(n-1,B,A,C);
}
}
int main(){
int n;
cin>>n;
move(n,'A','B','C');
return 0;
}
我们用 n=3 进行验证, 得到的结果如下:
第1次移动:把1号圆盘从A移到C
第2次移动:把2号圆盘从A移到B
第3次移动:把1号圆盘从C移到B
第4次移动:把3号圆盘从A移到C
第5次移动:把1号圆盘从B移到A
第6次移动:把2号圆盘从B移到C
第7次移动:把1号圆盘从A移到C
再用 n=4 进行验证,结果如下:
第1次移动:把1号圆盘从A移到B
第2次移动:把2号圆盘从A移到C
第3次移动:把1号圆盘从B移到C
第4次移动:把3号圆盘从A移到B
第5次移动:把1号圆盘从C移到A
第6次移动:把2号圆盘从C移到B
第7次移动:把1号圆盘从A移到B
第8次移动:把4号圆盘从A移到C
第9次移动:把1号圆盘从B移到C
第10次移动:把2号圆盘从B移到A
第11次移动:把1号圆盘从C移到A
第12次移动:把3号圆盘从B移到C
第13次移动:把1号圆盘从A移到B
第14次移动:把2号圆盘从A移到C
第15次移动:把1号圆盘从B移到C
因此对于此类问题的求解我们进行总结:
- 首先,解决问题需要理解问题,搞清楚连续发生的动作是什么
- 其次,要搞清楚不同次动作间的关系
- 最后,要搞清楚边界条件是什么
3.3 进行自动的分析
3.3.1 放苹果
有m个同样的苹果, 放入n个相同的盘子,允许有空的盘子,求共有多少种不同的放法k。
假设 f(m,n) = k, 首先我们对问题进行分析:
当n>m时,即盘子数量多于苹果数量时,那么无论怎么放置,都会有空盘的情况。那么问题就可以简化为求f(m,m)。
当n<m时,即盘子数量少于苹果数量时,我们此时又可以分为两种情况:
第一种情况是有空盘的情况。如果有空盘则至少有一个空盘子,那么我们又可以把问题等价为求==f(m,n-1)的问题。
第二种情况是没有空盘的情况,则每个盘子里至少会有一个苹果,因为每个盘子都会有至少一个苹果,所以这种情况我们可以把每个盘子都减去一个苹果,这个问题就会被转化为f(m-n,n)==的情况。
然后一直执行这个操作,直到最简单的情况即只剩下一个盘子和一个苹果的情况,即边界条件,程序停止自动分析。
具体的代码实现如下:
#include<iostream>
using namespace std;
int count(int m, int n){
if(m<=1||n<=1)
return 1;
if(m<n)
return count(m,m);
if(m>n)
return count(m, n-1) + count(m-n, n);
}
int main(){
int m, n;
int k = 0;
cout<<"请输入苹果的数量: ";
cin>>m;
cout<<"请输入盘子的数量: ";
cin>>n;
k = count(m,n);
cout<<"把"<<m<<"个苹果放入"<<n<<"个盘子中,一共有"<<k<<"种放法"<<endl;
return 0;
}
我们输入m=5,输入n=4,得到的结果如下:
把5个苹果放入4个盘子中,一共有6种放法
1. 5个苹果全放1个盘子 (5)
2. 4个苹果放1个盘子,1个苹果放另1个盘子 (4 + 1)
3. 3个苹果放1个盘子,2个苹果放另1个盘子 (3 + 2)
4. 3个苹果放1个盘子,1个苹果放第2个盘子,1个苹果放第3个盘子 (3 + 1 + 1)
5. 2个苹果放1个盘子,2个苹果放第2个盘子,1个苹果放第3个盘子 (2 + 2 + 1)
6. 2个苹果放1个盘,剩余3个分别放另3个盘子 (2 + 1 + 1 + 1)
3.3.2 逆波兰表达式
逆波兰表达式是一种把运算符前置的算术表达式:
2+3 的 逆波兰表达式为+23
(2+3)*4 的 逆波兰表达式为*+234
在逆波兰表达式中,不需要写括号,只要表达式写出来则计算顺序是确定的
请编写一个程序求解任意一个仅包含 +-*/ 四个运算符的逆波兰表达式的值
输入:
* + 11.0 12.0 + 24.0 35.0
输出:
1357.0
首先我们对问题进行分析,如果我们遇到一个运算符则该运算符一定能把后面的表达式分成两个部分,一直向后读输入的表达式,直到读到数字部分则完成一个计算部分。
为了更易于理解这个递归的过程 我们来举个例子:
* / + 12 36 + 1 3 - 15 8
首先我们假设有一个函数 notation() 可以解决这个问题
然后我们来模拟一下这个过程:
当我们调用notation()函数
-
程序先读入
*,则程序会将表达式分为两部分,将它们相乘notation() * notation() -
程序继续读入
/, 则程序会继续将表达式分为两部分,并将两部分相除notation() * notation() | notation() / notation() -
接着程序读入
+,则程序会继续将表达式分为两部分,并将两部分相加notation() * notation() | notation() / notation() | notation() + notation() -
接着程序向后读,读到的是数字,那么我们直接对数字进行相加
notation() * notation() | notation() / notation() | (12)+(36) -
程序继续向后读,读到的是
+,程序将后面的表达式分为两部分相加notation() * notation() | notation() / notation() | | (12)+(36) notation() + notation() -
程序继续向后读,读到的是数字
1和`3``,程序将数字返回notation() * notation() | notation() / notation() | | (12) + (36) (1) + (3) -
程序然后读入
-,程序将后面的表达式分为两部分相减notation() * notation() | | notation() / notation() notation() - notation() | | (12) + (36) (1) + (3) -
最后程序继续读,读入的是数字则返回数字
notation() * notation() | | notation() / notation() (15) - (8) | | (12) + (36) (1) + (3) -
当程序全部读入结束则返回结果
(12 + 36) / (1 + 3) * (15 - 8) = 48 / 4 * 7 = 84
因此,对于上述问题, 我们可以用代码实现为:
#include<iostream>
using namespace std;
double notation(){
char algo[10];
cin>>algo;
switch(algo[0]){
case '+':
return notation() + notation();
case '-':
return notation() - notation();
case '*':
return notation() * notation();
case '/':
return notation() / notation();
default:
return atof(algo);
}
}
int main(){
cout<<notation();
cout<<endl;
return 0;
}
对于解决利用递归进行自动分析的问题,我们通常:
- 先假设有一个函数可以解决这个问题
- 然后在用该函数之前,先分析如何解决,例如放苹果例子中的分情况讨论
- 最后我们要弄清楚最简单的情况,即边界条件时的答案是什么
总结
看了几个例子过后,其实这三种不同情况有时候是通用的,而且它们都有共同点就是需要知道求解目标的表达和最简单的边界情况是什么样的。在求解这类问题时,不用花时间搞清楚程序内部的每一步是怎么运行的,只需要知道初始和目标状态的表达式就可以。这也是为什么在我们对问题进行分析时,情况可能会比较复杂,但是在实际写代码的过程中,只有短短几行的原因。这几个例子每一个动手分析一遍并用代码实现一遍,那么对递归的理解会有质的提升。





















 6569
6569











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








