分治法解二维的最近对问题，算法分析与代码实现，蛮力法与分治法解决二维的最近对问题的区别

最新推荐文章于 2023-05-05 23:55:52 发布

勾栏听曲_0

最新推荐文章于 2023-05-05 23:55:52 发布

阅读量2.7k

点赞数 41

分类专栏：数据结构与算法文章标签：数据结构算法分治法 c语言

本文链接：https://blog.csdn.net/weixin_53050357/article/details/130132771

版权

数据结构与算法专栏收录该内容

17 篇文章 0 订阅

订阅专栏

🎊【数据结构与算法】专题正在持续更新中，各种数据结构的创建原理与运用✨，经典算法的解析✨都在这儿，欢迎大家前往订阅本专题，获取更多详细信息哦🎏🎏🎏

🪔本系列专栏 - 数据结构与算法_勾栏听曲_0

🍻欢迎大家 🏹 点赞👍 评论📨 收藏⭐️

📌个人主页 - 勾栏听曲_0的博客📝

🔑希望本文能对你有所帮助，如有不足请指正，共同进步吧🏆

🎇为人性僻耽佳句，语不惊人死不休。📈

分治法

算法思想

分治法可能是最著名的通用算法设计技术了。虽然它的名气可能和它那好记的名字有关，但它的确是当之无愧的:很多非常有效的算法实际上就是这个通用算法的特殊实现。其实，分治法是按照以下方案工作的。

(1)将一个问题划分为同一类型的若干子问题，子问题最好规模相同。
(2)对这些子问题求解(一般使用递归方法，但在问题规模足够小时，有时也会利用另一个算法)。
(3)有必要的话，合并这些子问题的解，以得到原始问题的答案。

分治法的流程可以参见下图，该图描述的是将一个问题划分为两个较小子问题的例子，也是最常见的情况(至少那些设计运行在单CPU机器上的分治算法是这样的)。

时间效率分析

在分治法最典型的运用中，问题规模为n的实例被划分为两个规模为n/2的实例。更一般的情况下，一个规模为n的实例可以划分为b个规模为n/b的实例，其中α个实例需要求解(这里，a和b是常量，a≥1，b>1)。为了简化分析，我们假设n是b的幂，对于算法的运行时间T(n)，我们有下列递推式:

T(n) =aT(n / b)+ f(n)

其中，f(n)是一个函数，表示将问题分解为小问题和将结果合并起来所消耗的时间(对于求和的例子来说，a = b = 2，f(n)= 1)。上述递推式被称为通用分治递推式(generaldivide-and-conquer recurrence)。显然，T(n)的增长次数取决于常量a和b的值以及函数f(n)的增长次数。在分析许多分治算法的效率时，可以应用下列定理来大大简化我们的工作。

主定理如果在递推式(5.1)中 f(n)e e(n*)，其中d≥0，那么

$T(n)\in \left\{\begin{matrix}\Theta (n^{d}) & a<b^{d}\\ \Theta (n^{d}\log n) & a=b^{d}\\ \Theta (n^{\log b^{a}}) & a>b^{d} \end{matrix}\right.$

其中，当a < $b^{d}$ 时，该问题的时间复杂度为n的d次方

当a = $b^{d}$ 时，该问题的时间复杂度为n的d次方乘一个对数级 $\log n$

当a > $b^{d}$ 时，该问题的时间复杂度为n的log b为底a次方

二维的最近对问题

二维的最近对问题是指在二维平面上有n个点，如何找到距离最近的两个点的问题。一种常用的解决方法是分治法，即将一个规模较大的问题分解为规模较小的子问题，先求解这些子问题，然后将各子问题的解合并得到原问题的解。

在之前的章节中，我们有学到蛮力法来解决一些问题，二维的最近对问题如果实用蛮力法来解决问题，那么时间效率为 $O(n^{2})$ 。但是使用分治技术可以用更高的时间效率来解决这个问题。

算法思路

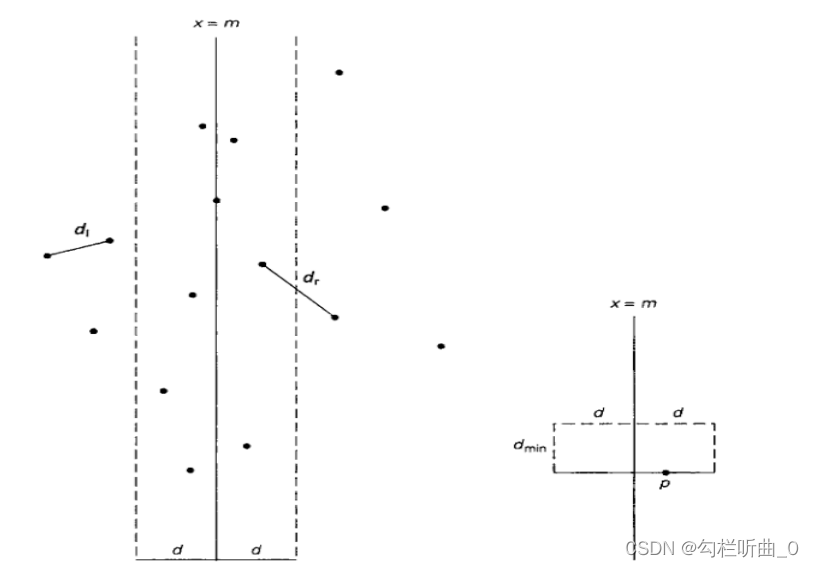
左图是最近对问题的分治算法的思想，右图是和点p距离小于d的点可能分布的矩形区域

具体步骤为：

将n个点按照x坐标排序，然后从中间划分为两个子集，分别求解左右两边的最近点对。
比较左右两边的最近点对的距离，取较小者作为当前的最近点对。
在中间区域内寻找可能存在的更近的点对，即在距离中线不超过当前最近点对距离的范围内，找出所有满足条件的点，并按照y坐标排序。
对于每个点，只需与它后面的7个点进行比较，如果发现更近的点对，则更新当前最近点对。
返回当前最近点对。

举例分析

我们举个例子，假设我们有以下6个点：

点	x坐标	y坐标
A	1	2
B	3	4
C	5	6
D	7	8
E	9	10
F	11	12

首先，我们按照x坐标排序，得到以下顺序：

A B C D E F

然后，我们从中间划分为两个子集，分别求解左右两边的最近点对。左边的子集是：

A B C

右边的子集是：

D E F

对于左边的子集，我们可以用暴力法求出最近点对是A和B，距离为根号8。对于右边的子集，我们也可以用暴力法求出最近点对是D和E，距离也是根号8。所以当前的最近点对距离是根号8。
接下来，我们在中间区域内寻找可能存在的更近的点对，即在距离中线不超过根号8的范围内，找出所有满足条件的点，并按照y坐标排序。中线的x坐标是6，所以我们只需要考虑C和D两个点。按照y坐标排序后，得到以下顺序：

C D

对于每个点，只需与它后面的7个点进行比较，如果发现更近的点对，则更新当前最近点对。在这个例子中，只有C和D两个点需要比较，它们的距离是根号8，与当前最近点对距离相等，所以不需要更新。
最后，我们返回当前最近点对，即A和B或者D和E。

代码实现

其中包括使用蛮力法（暴力破解）与分治法两种方法解决二维的最近对问题，大家可以通过运行代码来更直观的感受这两种方法的异同。

代码整体逻辑与分析：

定义了两个结构体，分别表示点和点对，以及一些辅助函数，如计算两点之间的距离，比较两个点对的距离，按照x坐标或y坐标排序的比较函数等。
实现了暴力法求解最近点对的函数，即遍历每个点，与后面的点进行比较，找出最近的点对。这个函数适用于点数较少的情况，时间复杂度是O(n^2)。
实现了分治法求解最近点对的函数，即将一个规模较大的问题分解为规模较小的子问题，先求解这些子问题，然后将各子问题的解合并得到原问题的解。这个函数适用于点数较多的情况，时间复杂度是O(nlogn)。具体的步骤如下：
- 如果点数小于等于3，直接用暴力法求解。
- 将n个点按照x坐标排序，然后从中间划分为两个子集，分别求解左右两边的最近点对。
- 比较左右两边的最近点对的距离，取较小者作为当前的最近点对。
- 在中间区域内寻找可能存在的更近的点对，即在距离中线不超过当前最近点对距离的范围内，找出所有满足条件的点，并按照y坐标排序。
- 对于每个点，只需与它后面的7个点进行比较，如果发现更近的点对，则更新当前最近点对。
- 返回当前最近点对。
主函数，用于测试代码。创建了一个测试用例，包含6个点，并调用分治法求解最近点对，并打印结果。

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

//定义一个点的结构体
typedef struct point {
    double x; //x坐标
    double y; //y坐标
} point;

//定义一个点对的结构体
typedef struct pair {
    point p1; //第一个点
    point p2; //第二个点
    double dist; //两点之间的距离
} pair;

//计算两点之间的距离
double distance(point p1, point p2) {
    return sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
}

//比较两个点对的距离，返回较小者
pair min(pair a, pair b) {
    if (a.dist < b.dist) {
        return a;
    } else {
        return b;
    }
}

//按照x坐标排序的比较函数
int compare_x(const void* a, const void* b) {
    point* p1 = (point*)a;
    point* p2 = (point*)b;
    if (p1->x < p2->x) {
        return -1;
    } else if (p1->x > p2->x) {
        return 1;
    } else {
        return 0;
    }
}

//按照y坐标排序的比较函数
int compare_y(const void* a, const void* b) {
    point* p1 = (point*)a;
    point* p2 = (point*)b;
    if (p1->y < p2->y) {
        return -1;
    } else if (p1->y > p2->y) {
        return 1;
    } else {
        return 0;
    }
}

//暴力法求解最近点对，适用于点数较少的情况
pair brute_force(point* points, int n) {
    pair min_pair; //最近点对
    min_pair.dist = INFINITY; //最近点对距离初始化为无穷大
    for (int i = 0; i < n; i++) { //遍历每个点
        for (int j = i + 1; j < n; j++) { //与后面的点进行比较
            double dist = distance(points[i], points[j]); //计算两点之间的距离
            if (dist < min_pair.dist) { //如果发现更近的点对，更新最近点对和最近点对距离
                min_pair.p1 = points[i];
                min_pair.p2 = points[j];
                min_pair.dist = dist;
            }
        }
    }
    return min_pair; //返回最近点对
}

//分治法求解最近点对，适用于点数较多的情况
pair divide_and_conquer(point* points, int n) {
    pair min_pair; //最近点对

    //如果点数小于等于3，直接用暴力法求解
    if (n <= 3) {
        return brute_force(points, n);
    }

    //将n个点按照x坐标排序，然后从中间划分为两个子集，分别求解左右两边的最近点对
    qsort(points, n, sizeof(point), compare_x); //按照x坐标排序
    int mid = n / 2; //中间位置的索引
    point mid_point = points[mid]; //中间位置的点

    pair left_pair = divide_and_conquer(points, mid); //求解左边子集的最近点对
    pair right_pair = divide_and_conquer(points + mid, n - mid); //求解
    //右边子集的最近点对
    min_pair = min(left_pair, right_pair); //比较左右两边的最近点对，取较小者作为当前的最近点对

    //在中间区域内寻找可能存在的更近的点对，即在距离中线不超过当前最近点对距离的范围内，找出所有满足条件的点，并按照y坐标排序
    point* strip = (point*)malloc(n * sizeof(point)); //创建一个动态数组，用于存放满足条件的点
    int size = 0; //记录满足条件的点的个数
    for (int i = 0; i < n; i++) { //遍历每个点
        if (fabs(points[i].x - mid_point.x) < min_pair.dist) { //如果该点距离中线不超过当前最近点对距离
            strip[size++] = points[i]; //将该点加入到动态数组中
        }
    }
    qsort(strip, size, sizeof(point), compare_y); //按照y坐标排序

    //对于每个点，只需与它后面的7个点进行比较，如果发现更近的点对，则更新当前最近点对
    for (int i = 0; i < size; i++) { //遍历每个点
        for (int j = i + 1; j < size && (strip[j].y - strip[i].y) < min_pair.dist; j++) { //与后面的7个点进行比较
            double dist = distance(strip[i], strip[j]); //计算两点之间的距离
            if (dist < min_pair.dist) { //如果发现更近的点对，更新最近点对和最近点对距离
                min_pair.p1 = strip[i];
                min_pair.p2 = strip[j];
                min_pair.dist = dist;
            }
        }
    }

    free(strip); //释放动态数组的内存空间
    return min_pair; //返回最近点对
}

//主函数，用于测试代码
int main() {
    //创建一个测试用例，包含6个点
    point points[] = {{1, 2}, {3, 4}, {5, 6}, {7, 8}, {9, 10}, {11, 12}};
    int n = sizeof(points) / sizeof(points[0]); //计算点的个数

    pair result = divide_and_conquer(points, n); //调用分治法求解最近点对

    printf("The closest pair is (%.2f, %.2f) and (%.2f, %.2f), and the distance is %.2f.\n", result.p1.x, result.p1.y, result.p2.x, result.p2.y, result.dist); //打印结果

    return 0;
}

勾栏听曲_0

关注

41
点赞
踩
54

收藏

觉得还不错? 一键收藏
打赏
41
评论
分治法解二维的最近对问题，算法分析与代码实现，蛮力法与分治法解决二维的最近对问题的区别

利用分治法解决二维的最近对问题，蛮力法解决二维的最近对问题的两种方法算法分析与代码实现，以及分治法下解决二维的最近对问题的实例分析。解析分治算法的思想，分治法的流程，分治法是如何实现的，利用分治算法的主定理分析分治算法在不同情况下的时间复杂度。
复制链接

扫一扫