1.1 函数的概念、反函数（一一映射）、单调/奇偶/周期/有界/无界函数

一、 函数基础

1. 函数两个基本要素？ (定义域和对应法则)

2. 两函数的复合条件？ (外层函数的定义域和内层函数的值域的交集必须非空)

   

二、 反函数

1. 判断某函数是否有反函数？ (单调函数一定有反函数；但反函数不一定单调)

   

2. 判断有反函数的充要条件？ (定义域与值域之间是一一映射的)

3. 图形属性？
   y = f(x) 和 y = f⁻¹(x) 的图形关于直线 y = x 对称。
   y = f(x) 和 x = f⁻¹(y) 是同一个函数。（图形重合）
   

4. 恒等映射？（利用该性质做题 常为考点）

   • f[f⁻¹(x)] = x
   • f⁻¹[f(x)] =x
     

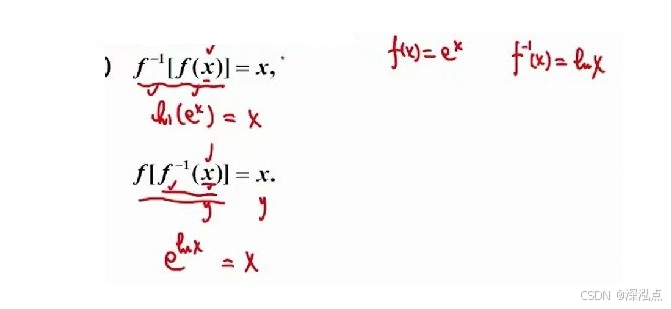
5. 利用一元二次方程求解反函数 ？（掌握一元二次求根公式，此处舍去负数根）
   

三、 初等函数

1. “基本初等函数”有哪些？ (幂函数、指数函数、对数函数、三角函数、反三角函数)

2. 初等函数的定义？(一个由常数和基本初等函数通过有限次四则运算和复合运算得到的，并且可以用一个解析式表达的函数)

3. 函数的性质？ (单调性、奇偶性、周期性、有界性)

   • 奇偶性运算
     • 奇 + 奇 = 奇； 偶 + 偶 = 偶；
     • 奇 × 奇 = 偶； 偶 × 偶 = 偶； 奇 × 偶 = 奇；

4. 如果奇函数 f(x) 在 x=0 处有定义，则 f(0) = 0。

5. 证明奇函数 (示例)？ (利用分子分母有理化、商的对数等于对数的差)
   

四、周期函数与有界函数

1. 常见的周期函数？
2. 关于周期函数的一个重要推论？

• sin x, cos x 的周期为 2π； sin 2x, sin x 的周期为 π。
• 若 f(x) 以 T 为周期，则 f(ax + b) 以 T/|a| 为周期。

3. 常见的有界函数？

   • |sin x| ≤ 1
   • |cos x| ≤ 1
   • |arcsin x| ≤ π/2
   • |arctan x| < π/2
   • |arccos x| ≤ π

4. 反三角函数导数公式？ (表2)

5. 着重记忆常用的有界反三角函数：arctan x < π/2.

6. 证明是无界函数 (示例)？ (通常代入特殊值，如 2nπ + π/2)
   

五、常考题型

1. 常考题型？

   • 函数的有界性、单调性、周期性及奇偶性的判定。
   • 复合函数的有界性、单调性、周期性及奇偶性的判定。

2. 例题