离散数学-逻辑

1.命题逻辑的基本概念

1.1 命题与连接词

1.1.1命题

非真即假的陈述句

1.1.2真值

命题的判断结果

1. 一个命题如果是对的或正确的,则称为真命题,其真值为“真(ture),常用T或1表示；一个命题如果是错的或不正确的,则称为假命题,其真值为“假”(false),常用F或0表示

2. 任何命题的真值都是唯一的

例：

1.1.3命题变元（命题变项）

通常用小写英文字母p,q,r,...或带有下标的小写字母P₁,p₂,p₃,...来表示命题,称为命题变元或命题变项

1.命题变项与命题的区别：

• 命题有具体的含意和确定的真值
• 命题变项只有明确表示某个命题时才有具体的含意和确定的真值

2.命题变项一般只表示一个抽象的命题,其真值可能是T也可能是F，但通常也简称命题变项为命题

3.不能再分解的命题称为简单命题或原子命题，一般形式是“......是......”。由原子命题组合而成的命题称为复合命题

例：

• ∏和e都是无理数
• 6和8至少有一个是合数
• 说刘老师讲课不好是不正确的
• 不下雨我就去买书。

1.1.4命题联结词（命题运算符）

将命题连接起来的方式叫做命题联结词或命题运算符

1.设p为命题,否定词“¬”是一元联结词

• ¬p读作"非p"或“p的否定"
• 若p的真值为真,则¬p的真值为假;反之,若p为假,则¬p为真
• 否定联结词的含意相当干自然语言中的“不”、“没有”、无”、“否定”,“井非”“取反"等

2.设p,q为命题,合取词"∧"是二元联结词

• p∧q读作“p与q”或“p,q的合取"
• 当且仅当p,q的真值均为真时,p∧q的真值为真
• 合取联结词的含意相当于自然语言中的“p和q”、“p与q、“p且q、“p,同时q、“p并且q“p以及q、“p而且q”、“既p,又q、“不但p,而且q”、“尽管p,依然q”、“虽然p,但是q”等

3.设p,q为命题,析取词"∨"是二元联结词

• pVq读作"p或q”或“p,q的析取"
• 当且仅当p,q的真值均为假时,pVq的真值为假
• 析取联结词的含意相当于自然语言中的“p或者q",“要么p,要么q”,“不是p就是q”等。

4.设p,q为命题,异或词"p⊕q”是二元联结词

• p⊕q读作“p异或q
• 当且仅当p,q的真值相同时,p⊕q的真值为假
• “异或“也称“不可兼或"

5.设p.q为命题,蕴涵词“→"是二元联结词

• p→q读作“若p则q"
• 当且仅当p的真值为真、q的真值为假时,p→q的真值为假
• p称作前提,q称作结论
• 蕴联结词的含意相当于自然语言中的“如果p则q"、“因为p,所以q、“只要p,就q"、“只有q,才p、“仅当q,则p","p是q的充分条件”、“q是p的必要条件"“既然p那么q"等

6.设p,q为命题,等价词"＜＝＞"是二元联结词

• p＜＝＞q读作“p当且仅当q”或“p,q等价
• 当且仅当p.q的真值相同时,p＜＝＞q的真值为真
• “等价“也称作双条件.
• 等价联结词的含意相当于自然语言中的"p,当且仅当q”“p是q的充分必要条件”、“p,q含义相同”等。

1.1.5命题公式及其分类

复合命题是由命题变项、逻辑联结词和括号等符号组成的符号串;但反过来,由这些符号组成的符号串并不一定都是命题

 

 

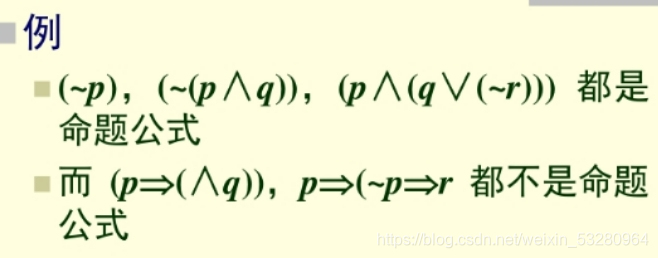
 设A为命题公式,B为A中的一个连续的符号串,且B为命题公式,则称B为A的子公式

 命题公式不是命题,只有当公式中的每一个命题变项都被赋以确定的真值时,公式的真值才被确定,从而成为一个命题

 

• 重言式一定是可满足式,但反之不真
• 任意两个重言式的析取或合取仍然是重言式
• 任意两个矛盾式的析取或合取仍然是矛盾式

1.1.6真值表

一个命题公式在每种真值指派(每种命题变项取值的组合)上的值可以直观地用真值表来计算和表示

为方便构造真值表,特约定如下:

(1)命题变项按字典序排列

(2)对每个真值指派,以二进制数从小到大或从大到小顺序列出

(3)若公式较复杂,可先列出各子公式的真值,最后列出所求公式的真值

p	q	¬p	p∧q	pVq	p⊕q	p→q	p＜＝＞q
T	T	F	T	T	F	T	T
T	F	F	F	T	T	F	F
F	T	T	F	T	T	T	F
F	F	T	F	F	F	T	T

 1.1.7命题的符号化

把一个用自然语言表述的命题表示为由命题公式的形式,称为命题的符号化,这是进行推理演算的首要步骤。命题的符号化一般经过如下三个步骤:

1. 找出各原子命题,将原子命题符号化

2. 找出命题中各联结词,将联结词符号化

3. 将原子命题和联结词组成一个复合命题

2.命题逻辑等值演算

2.1等值式

1.设A,B为两个命题公式,若A<=>B为一个重言式,则称A与B等值或逻辑等价,记作A ≡B,称A≡B为等值式

2.判断两个命题公式是否等值主要有两种方法

• 真值表法：将两个公式的真值表列出,判断输出列是否相同

• 等值演算法：由已知的等值式推演出新的等值式

3.等值演算不能直接证明两个公式不等值。证明两个公式不等值的基本思想是找到一个真值指派使一个成真,另一个成假

4.例  p∨(p∧q)≡p

p	q	p∧q
T </