李哥AI第四章深度学习

回归任务和分类任务的区别：

为什么分类任务不用一个输出值：

因为在一个连续的数轴上，利用预测值和类别值更近的方法各个类别与预测点的距离各不相同，即各个类别不等价。在分类任务中只有是和不是的区别，没有哪一个更像的区别。

如何分类输出

有几个类就要有几个输出

卷积神经网络：

图片是矩阵：

直接将图片转化为矩阵展开数据过大，非常容易过拟合。

卷积神经网络的过程图：

什么是卷积核

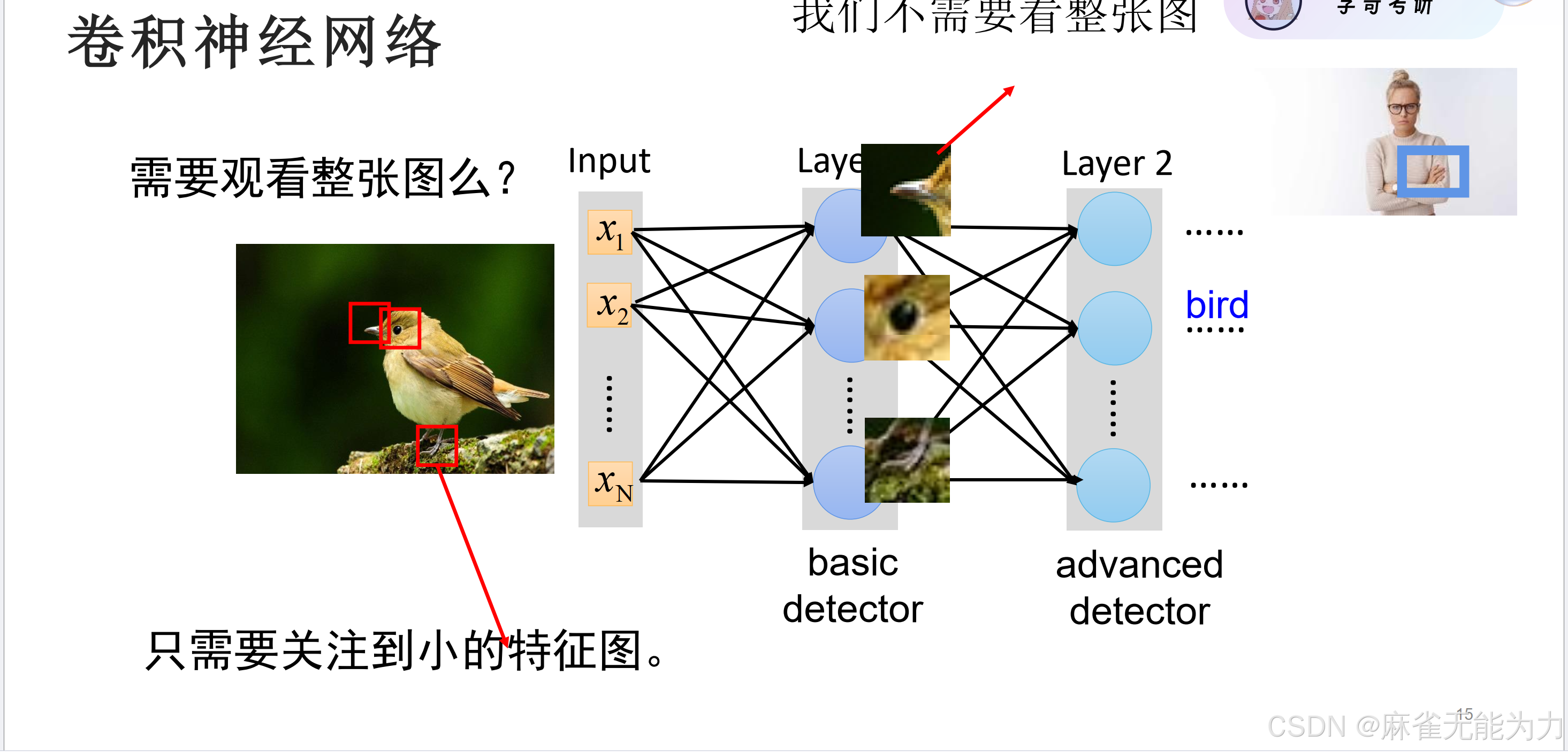
比如在这张鸟的图片中，鸟嘴，鸟眼就可以当成一个卷积核。

使用padding保持卷积后特征图大小不变：

可以增加卷积和的大小和卷积核数量，增减训练的参数：

1.特征图长宽计算公式：

I：输入特征图长度

k：卷积核长度

O：输出特征图长度：

padding直接加在输入特征图上

2.

若该公式成立，则 I = O即输入特征图与输出特征图大小不变

3.一层卷积核参数的计算公式：

卷积核数量*卷积核层数*卷积核高度*卷积核宽度

以下是练习题：

降低特征图尺寸的方法：

特征图尺寸过大会使参数过多，有以下两种方式降低特征图的尺寸

方法一：

降低采样，设置步长：

计算公式：

该方法会丢失数据，引入计算；

方法二：

池化：

两种池化方式：

卷积神经网络的实现：

用卷积核数量改变层数，用池化改变特征图大小

将特征图卷小后就可以平铺展开，在进行回归。

计算loss

首先要转化为概率分布

然后计算交叉熵损失

下面是一个用来理解多分类公式的实例：

卷积神经网络的发展：

一些可以提出的创新点：

drop out

使某些节点在训练时不发挥作用，可以避免过拟合，减小计算量。

归一化：

经典模型AlexNet的解析：

AlexNet

注：Pool中的第一个数字表示单次池化范围，第二个数字表示池化步长

参考代码：

class MyAlexNet(nn.Module):                         #定义模型中样式
    def __init__(self):
        super(MyAlexNet, self).__init__()
        self.relu = nn.ReLU()
        self.drop = nn.Dropout(0.5)

        self.conv1 = nn.Conv2d(in_channels=3, out_channels=64, kernel_size=11, stride=4,padding=2)
        self.pool1 = nn.MaxPool2d(3, stride=2)
        self.conv2 = nn.Conv2d(64,192,5,1,2)
        self.pool2 = nn.MaxPool2d(3, stride=2)

        self.conv3 = nn.Conv2d(192,384,3,1,1)

        self.conv4 = nn.Conv2d(384,256,3,1,1)

        self.conv5 = nn.Conv2d(256, 256, 3, 1, 1)

        self.pool3 = nn.MaxPool2d(3, stride=2)
        self.adapool = nn.AdaptiveAvgPool2d(output_size=6)

        self.fc1 = nn.Linear(9216,4096)

        self.fc2 = nn.Linear(4096,4096)

        self.fc3 = nn.Linear(4096,1000)

    def forward(self,x):                        #使用样式构造模型

        x = self.conv1(x)
        x = self.relu(x)
        x = self.pool1(x)

        x = self.conv2(x)
        x = self.relu(x)
        x = self.pool2(x)


        x = self.conv3(x)
        x = self.relu(x)
        print(x.size())
        x = self.conv4(x)
        x = self.relu(x)
        print(x.size())
        x = self.conv5(x)
        x = self.relu(x)
        x = self.pool3(x)
        print(x.size())
        x= self.adapool(x)
        x = x.view(x.size()[0], -1)

        x = self.fc1(x)
        x = self.relu(x)

        x = self.fc2(x)
        x = self.relu(x)

        x = self.fc3(x)
        x = self.relu(x)

        return x

VGGNet

参考代码：

class vggLayer(nn.Module):
    def __init__(self,in_cha, mid_cha, out_cha):
        super(vggLayer, self).__init__()
        self.relu = nn.ReLU()
        self.pool = nn.MaxPool2d(2)
        self.conv1 = nn.Conv2d(in_cha, mid_cha, 3, 1, 1)
        self.conv2 = nn.Conv2d(mid_cha, out_cha, 3, 1, 1)

    def forward(self,x):
        x = self.conv1(x)
        x= self.relu(x)
        x = self.conv2(x)
        x = self.relu(x)
        x = self.pool(x)
        return x

ResNet

残差链接的作用：避免梯度消失

梯度消失：里层的参数计算梯度时是多次求偏导的结果，当偏导小于1时会越乘越小，最后趋近于0，为了避免这种情况采用f(x) + x的形式可以保证求偏导的结果至少大于1.

这也是为什么relu比sigmoid好的原因：

在右端sigmoid的梯度已经接近于0了

1乘1卷积：

作用1：降低参数，减小计算量

原参数：256 * 256  * 3 * 3

降维后参数：256 * 64 * 1 * 1+ 64 * 64 * 3  * 3 + 64 * 256 * 1  *  1

作用2：解决残差链接中输入输出特征图维度不同的问题：