文章目录
问题描述
给定n种物品和一背包。物品i的重量是wi>0,其价值为vi>0,背包的容量为c。问应如何选择装入背包中的物品,使得装入背包中物品的总价值最大?
1.回溯法求解
搜索空间:
子集树(完全二叉树)
约束函数(进包用):
如果当前背包中的物品总重量是cw,前面k-1件物品都已经决定是否进包,那么第k件物品进包的条件是:cw +w:≤M。
上界函数(不进包用):
设cp是当前价值,r是将剩余物品的价值之和.cp十r为对应装包方案集的上界。
上界函数(不进包用):
设cp是当前价值,r是将剩余物品及剩余载重量对应的背包问题的最优值。cp十r为对应装包方案集的上界。
实例
例如,对于n=4时的0-1背包问题,考虑下面的具体实例:
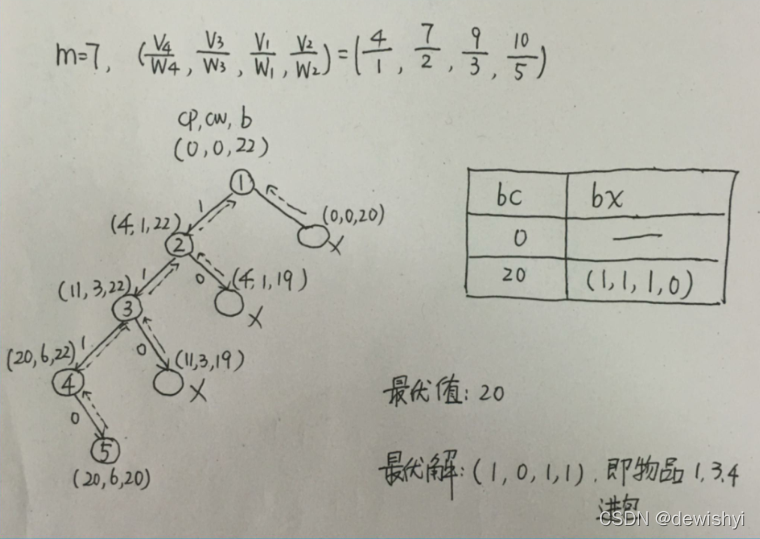
w=[3,5,2,1], v=[9,10,7,4],m=7.
解:将物品vi/wi递减排序,(v4/w4,v3/w3,v1/w1,v2/w2)=(4/1,7/2,9/3,10/5)
按排序后的物品顺序dfs完全二叉树求解。设bc、bx分别表示当前的最优值和最优解,(cp, cw, b)分别表示各结点对应包的当前价值、重量及装包方案上界。第i个物品能进包的约束条件为cw+wli]<=m,上界函数为对应背包问题的最优值+cp.进包的条件是约束条件,不进包的条件是b>bc(限界函数)。搜索过程如下(结点号表示其产生顺序,旁边(cp, cw, b)标注):得
bx=(1, 1, 1,0)
bc=20
对应到原物品号,得最优解:
x=(1, 0, 1,1)
相关代码:
#include <iostream>
#include <stdio.h>
using namespace std;
typedef struct{
int v;
int w;
int no;
}goods;
int n,c;//物品数量,背包容量
int *x;//当前解
goods *a;//物品
int bv,*bx;//最优值,最优解
int cc,cw;//当前价值,当前重量
int cmp(goods a,goods b)//约定sort 所用cmp函数
{
return a.v*b.w>=a.w*b.v;
}
float Bound(int step){//贪心算法求得当前状态下对应背包的最优值
int i,m=c-cw;
float b=cc;
for(i=step; i<=n&&a[i].w<=m;i++)
b+=a[i].v, m-=a[i].w;
if(i<=n)
b+=(m*1.0/a[i].w)*a[i].v;
return b;
}
void dfs(int step){
int i;
if(step>n){//叶子结点
if(cc>bv){
bv=cc;
for(i=1;i<=n;i++)bx[a[i].no]=x[i];//序号还原
}
return;//回头
}
if(cw+a[step].w<=c){//满足约束条件,进入左子树
x[step]=1;
cc+=a[step].v;cw+=a[step].w;
dfs(step+1);
cc-=a[step].v;cw-=a[step].w;//恢复现场
}
if(Bound(step+1)>bv){//满足上界条件,进入右子树
x[step]=0;
dfs(step+1);
return;
}
}
int main(){
int i;
cout<<"请输入物品个数n:"<<endl;
cin>>n;
a=new goods[n+1];
bx=new int[n+1];
x=new int[n+1];
cc=0;
cw=0;
bv=0;
cout<<"请输入背包容量c:"<<endl;
cin>>c;
for(i=1;i<=n;i++)a[i].no=i,x[i]=0;
printf("请依次输入%d个物品的价值:\n",n);
for(i=1;i<=n;i++)cin>>a[i].v;
printf("请依次输入%d个物品的重量:\n",n);
for(i=1;i<=n;i++)cin>>a[i].w;
dfs(1);
printf("最优价值为:%d\n",bv);
cout<<"最优解为:"<<endl;
for(i=1;i<=n;i++)cout<<bx[i]<<'\t';
cout<<endl;
return 0;
}
2.分支限界法求解
基本思想:
分支限界法的基本思想是对有约束条件的最优化问题的所有可行解空间适当进行地搜索。
其搜索过程可用一棵树表示,常见的有子集树和排列树。树的根结点即是全部可行解,把全部可行解不断分割成越来早越小的子集(分支),并且为每个子集内的解计算一个下界或上界(定界)。
在每次分支之后,对那些界限超出已知可行解值的那些子集不再做进一步的分支。
这个过程一直进行到找出可行解且该可行解的值不小于(大于)任何子集的界限为止。
分支限界法有两种策略
1.队列式(FIFO)分支限界法将活结点表组织成一个队列,并按队列的先进先出原则选取下一个结点作为当前扩展结点。
2.优先队列式分支限界法:
将活结点表组织成一个优先队列,并按优先队列给结点规定的优先级选取优先级最高的下一个结点作为当前扩展结点。
实例
此处采用优先队列求解,对于上文的例子,图解为:

首先序号1出队列,对于物品1有两种选择,1或0,则2,3入队列;由于2的上界22大于3的上界,则2出队列,4,5入队列,然后在所有结点中取上界最大的结点出队列,带来的两种或1种选择出队列,依次类推…
当结点8完成时,更新最优值和最优解,对于上界不大于20的选择进行剪支。
相关代码
#include <algorithm>
#include <iostream>
using namespace std;
#include<queue>//队列的相关函数调用
#include<stdio.h>
struct node{
int cc,cw;//当前价值和载重量
int step;//第step个物品
int *x;
float upcc;//上界
bool operator <(const node &b) const
{
return upcc<b.upcc;
}
};
typedef struct {
int w,v,no;
}goods;//物品
int n,c;//物品个数,背包容量
goods *a;//
int bv,*x,*bx;//最有值,当前解,最优解
int cmp(goods a,goods b)//约定sort 所用cmp函数 ,排序
{
return a.v*b.w>=a.w*b.v;
}
float bound(node st)//搜索限界函数
{//贪心算法求得背包问题的最优值
int i,m=c-st.cw;
float b=st.cc;
for(i=st.step; i<=n&&a[i].w<=m;i++)
{b+=a[i].v; m-=a[i].w;}
if(i<=n)
b+=(m*1.0/a[i].w)*a[i].v;//
return b;
}
void pfs(){//pfs搜索函数
node now,next;//当前结点,下一结点
int i,ns;
priority_queue <node> Q; //优先队列Q
now.cc=now.cw=0;now.step=1;now.x=new int[now.step];now.upcc=bound(now);//初始化
Q.push(now);//进队列
while(!Q.empty())//队不空
{
now=Q.top();Q.pop();//
if(now.upcc<=bv)break;//finished
ns=now.step;
if(ns==n+1)// 更新最优值最优解
{
if(now.cc>bv)//
{bv=now.cc; for(i=1;i<=n;i++) bx[i]=now.x[i];}
continue;
}//
//1-branch 右子树
if(a[ns].w+now.cw<=c){
next.cc=now.cc+a[ns].v;next.cw=now.cw+a[ns].w;
next.step=ns+1;next.upcc=now.upcc;//
next.x=new int[next.step]; for(i=1;i<ns;i++)next.x[i]=now.x[i];//
next.x[ns]=1;//
Q.push(next);//
}
//0-branch 左子树
next.cc=now.cc;next.cw=now.cw;next.step=ns+1;
float t=bound(next);
if(t>bv)//
{
next.upcc=t;
next.x=new int[next.step]; for(i=1;i<ns;i++)next.x[i]=now.x[i];
next.x[now.step]=0;
Q.push(next);//
}
}//while
}//pfs
int main(){
int i;
cout<<"请依次输入物品个数n和背包容量c:"<<endl;
cin>>n>>c;
x=new int[n+1]; bx=new int[n+1]; a=new goods[n+1];
cout<<"请依次输入物品重量:"<<endl;
for(i=1;i<=n;i++)cin>>a[i].w;
cout<<"请依次输入物品价值:"<<endl;
for(i=1;i<=n;i++)cin>>a[i].v;
for(i=1;i<=n;i++)a[i].no=i;
sort(a+1,a+1+n,cmp);
pfs( );
for(i=1;i<=n;i++)x[a[i].no]=bx[i];//序号还原
cout<<"\nThe best solution is:";
for(i=1;i<=n;i++)printf("%d ",x[i]);
cout<<"\nThe best value is: "<<bv<<endl<<endl;
delete []x;
delete []bx;
delete []a;
return 0;
}
3.动态规划法求解
给定c>0,wi>0,vi>0;1<=i<=n.求一个n元向量(x1,x2…xn),使得:
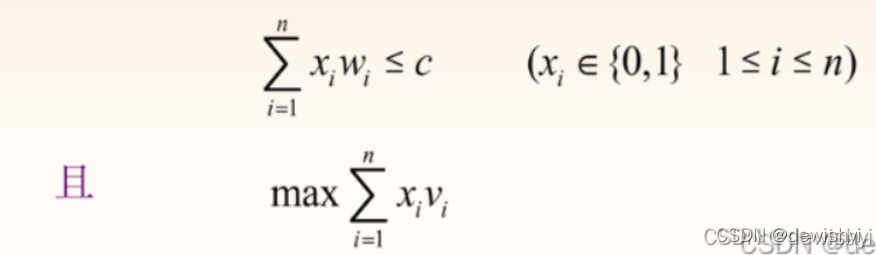
分析最优解的结构
假设(y1,y2 ,… , yn)是上述所给O-1背包问题的一个最优解,则(y2 , … , yn)必定是下面子问题的最优解:
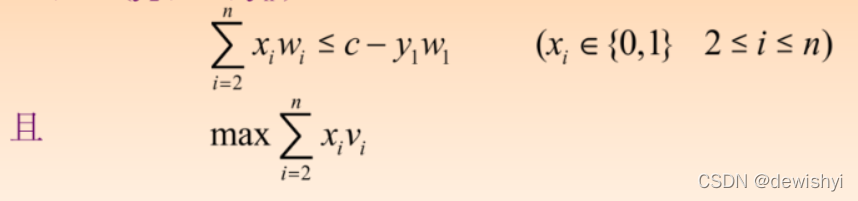
建立最优值的递归关系
设所给0-1背包问题的子问题:背包载重量为j,可选物品为i,i+1,…,n时的0-1背包问题的最优值为m[i][j],原问题目求m[1][c].
根据最优解的结构,我们很容易得出下列关于m[i][i]的递归方程:
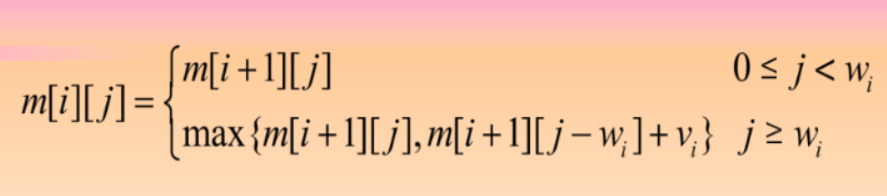
当i=n时,可选物品只有n一个,此时显然有:
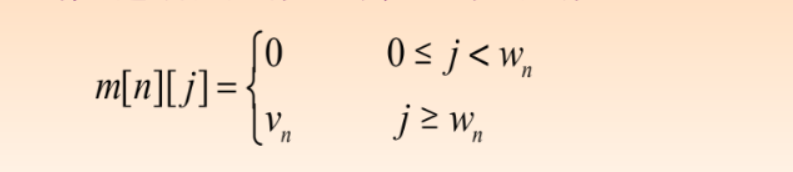
根据上述递归式, m[i][j]可能与m[i+1][j]相等,此时显然是对应物品i不装包的情况,反之对应物品i装包的情况.为了求出最优解,我们用b[i][j]来记载m[i][j]的取值情况:

实例
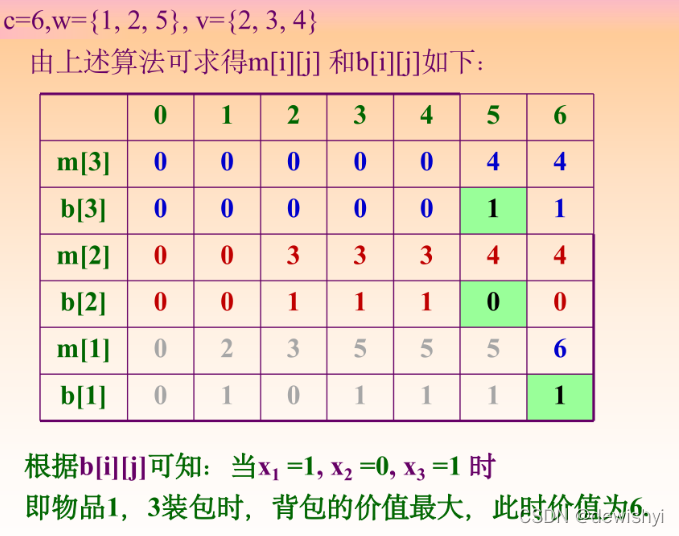
相关代码
#include <algorithm>
#include <iostream>
#include<stdio.h>
using namespace std;
int Bestv(int c,int *w,int *v,int n,int**m,int**b)//求最优解
{//背包容量,重量矩阵,价值矩阵,物品个数
int i,j;
for(j=0;j<w[n];j++)m[n][j]=b[n][j]=0;//对m(n,j)处理
for(j=w[n];j<=c;j++){m[n][j]=v[n]; b[n][j]=1;}
for(i=n-1;i>=2;i--)
{
for(j=0;j<w[i];j++){m[i][j]=m[i+1][j]; b[i][j]=0;}
for(j=w[i];j<=c;j++)
{
m[i][j]=m[i+1][j]; b[i][j]=0;
if(v[i]+m[i+1][j-w[i]]>m[i][j])
{m[i][j]=v[i]+m[i+1][j-w[i]]; b[i][j]=1;}
}
}
m[1][c]=m[2][c];b[1][c]=0;
if(w[1]<=c)
{
if(v[1]+m[2][c-w[1]]>m[1][c])
{
m[1][c]=v[1]+m[2][c-w[1]];b[1][c]=1;}
}
return m[1][c];
}
void Bests(int ** b,int *w,int *x,int n,int c)//求最优解x
{
int i,j;
j=c;
for(i=1;i<=n;i++)
{
x[i]=b[i][j];
j-=x[i]*w[i];
}
}
int main(){
int i,c,n,*w,*p,**m,**b,*x;
cout<<"请依次输入物品个数n和背包容量c:"<<endl;
cin>>n>>c;
w=new int[n+1]; p=new int[n+1];
cout<<"请依次输入物品重量:"<<endl;
for(i=1;i<=n;i++)cin>>w[i];
cout<<"请依次输入物品价值:"<<endl;
for(i=1;i<=n;i++) cin>>p[i];
m=new int *[n+1]; b=new int *[n+1];
for(i=1;i<=n;i++)
{m[i]=new int[c+1]; b[i]=new int[c+1];}
cout<<"Best Value: "<<Bestv(c, w, p, n,m, b)<<endl;
x=new int[n+1];
Bests(b,w,x,n,c);
cout<<"Best Solution: ";
for(i=1;i<=n;i++)cout<<x[i]<<'\t';
cout<<endl;
fclose(stdin);
return 0;
}




















 3万+
3万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








