如何用 python 实现支持向量机（SVM）

一、原理

支持向量机的原理简单概括来说，就是在样本空间寻找最佳分类面即超平面，将训练样本分开。对于样本空间，可能存在多个划分超平面将两类训练样本分开。我们就想找到一个最优的平面能够使样本正确分类，即找到一个平面使得边缘距离最小，如图2.1所示：

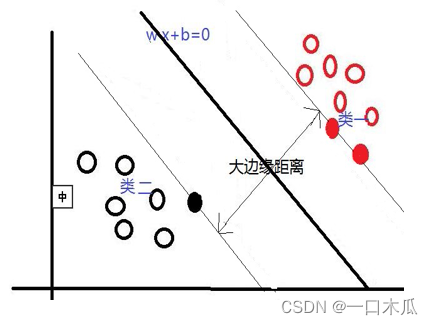
 图2.1：支持向量机原理图

支持向量机也就是一个二次规划问题，主要采取SMO算法，因为SMO算法能够将大优化问题分解为多个小优化问题进行求解，在这些小优化问题通常比较容易求解，并且对他们进行顺序求解的结果和它们作为整体求解的结果一致，在结果完全相同时，SMO算法求解的时间要较短。

 二、代码

导入库，其中从sklearn.preprocessing导入PolynomialFeatures用于构建多项式，以便构建非线性边界：

import matplotlib.pyplot as plt
import numpy as np
from sklearn.preprocessing import PolynomialFeatures

主程序：

# 读取数据，如果你要在自己电脑上运行此程序，首先确保电脑上有此文件，然后文件路径改为自己电脑上的路径
data = np.genfromtxt(r'C:\Users\yuhaowei\Desktop\1\赛题1：Python编程实现机器学习公式—附件所需附件.txt', delimiter=',')
# 读取第一列
x_data = data[:, 0]
# 读取第二列
y_data = data[:, 1]
# 多项式化，选择二次多项式作为核函数，为后面的支持向量机做准备
poly_reg_1 = PolynomialFeatures(degree=3)
data_matrix_1 = poly_reg_1.fit_transform(data[:, :-1])
poly_reg = PolynomialFeatures(degree=2)
data_matrix = poly_reg.fit_transform(data[:, :-1])
print(data_matrix.shape)
# 读取标签
label_data = data[:, 2]

n = len(x_data)
# 根据标签画数据的散点图
for i in range(n):
    if label_data[i] == 1:
        plt.scatter(x_data[i], y_data[i], c='b')
    else:
        label_data[i] = -1
        plt.scatter(x_data[i], y_data[i], c='r')

# 子程序，其中i使alpha的下标，m使alpha的数目，只要输入i，函数就会随机选择alpha
def selectJrand(i, m):
    j = i
    while (j==i):
        j = int(np.random.uniform(0, m))
    return j
# 子函数，用于调整大于H或小于L的alpha值
def clipAlpha(aj, H, L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj
# 主程序SMO算法，输入dataMatIn为多维数据，classLabels为数据标签，c为常数，toler为容错率，maxIter为最大循环次数
def smoSimple(dataMatIn, classLabels, c, toler, maxIter):
    dataMatrix = np.mat(dataMatIn)
    labelMat = np.mat(classLabels).transpose()
    b = 0
    m, n = dataMatrix.shape
    alphas = np.zeros((m, 1))
    iter = 0
    # 如果alpha可以更改，进入优化过程
    while iter < maxIter:
        alphaPairsChanged = 0
        for i in range(m):
            fxi = float(np.multiply(alphas, labelMat).T *
                        (dataMatrix * dataMatrix[i, :].T)) + b
            Ei = fxi - float(labelMat[i])
            if ((labelMat[i] * Ei < -toler) and (alphas[i] < c)) or ((labelMat[i] * Ei > toler) and alphas[i] > 0):
                # 随机选择第二个alpha
                j = selectJrand(i, m)
                fxj = float(np.multiply(alphas, labelMat).T *
                            (dataMatrix * dataMatrix[j, :].T)) + b
                Ej = fxj - float(labelMat[j])
                alphaIold = alphas[i].copy()
                alphaJold = alphas[j].copy()
                # 保证alpha在0和c之间
                if labelMat[i] != labelMat[j]:
                    L = max(0, alphas[j] - alphas[i])
                    H = min(c, c + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - c)
                    H = min(c, alphas[j] + alphas[i])
                if L == H:
                    #  print('L == H')
                    continue
                eta = 2.0 * dataMatrix[i, :] * dataMatrix[j, :].T - dataMatrix[i, :] * dataMatrix[i, :].T - \
                      dataMatrix[j, :] * dataMatrix[j, :].T
                # 对i修改，修改量与j相同，但方向相反
                if eta >= 0:
                    #  print('eta >= 0')
                    continue
                alphas[j] -= (labelMat[j] * (Ei - Ej) / eta).flatten().A[0]
                alphas[j] = clipAlpha(alphas[j], H, L)
                if abs(alphas[j] - alphaJold) < 0.00001:
                    #  print('j not moving enough')
                    continue
                # 给两个alpha值设置一个常数项b
                alphas[i] += (labelMat[j] * labelMat[i] * (alphaJold - alphas[j])).flatten().A[0]
                b1 = b - Ei - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[i, :].T - \
                    labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[i, :] * dataMatrix[j, :].T
                b2 = b - Ej - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[j, :].T - \
                     labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[j, :] * dataMatrix[j, :].T
                if (0 < alphas[i]) and (c > alphas[i]):
                    b = b1
                elif (0 < alphas[j]) and (c > alphas[j]):
                    b = b2
                else:
                    b = (b1 + b2) / 2
                    alphaPairsChanged += 1
                    #  print('iter: %d i:%d, pairs changed %d' % (iter, i, alphaPairsChanged))
        if alphaPairsChanged == 0:
            iter += 1
        else:
            iter = 0
            #  print('iteration number: %d' % iter)
    return b, alphas

b_1, alphas_1 = smoSimple(data_matrix_1, label_data, 0.6, 0.001, 1000)
b, alphas = smoSimple(data_matrix, label_data, 0.6, 0.001, 1000)
# 根据参数alphas求权重
w = 0
for i in range(n):
    w += alphas_1[i] * label_data[i] * data_matrix_1[i]
print(w)

三、可视化结果图

代码如下所示：

# 画图，求x，y的最大最小值
x_min, x_max = x_data.min() - 1, x_data.max() + 1
y_min, y_max = y_data.min() - 1, y_data.max() + 1
# 网格化
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))
z = b_1 + w[0] + w[1] * xx + w[2] * yy + w[3] * xx ** 2 + w[4] * xx * yy + w[5] * yy ** 2 + w[6] * xx ** 3 \
    + w[7] * xx ** 2 * yy + w[8] * xx * yy ** 2 + w[9] * yy ** 3
# 利用等高线画出分类边界
plt.contour(xx, yy, z, [0])
plt.show()

n = len(x_data)
# 根据标签画数据的散点图
for i in range(n):
    if label_data[i] == 1:
        plt.scatter(x_data[i], y_data[i], c='b')
    else:
        label_data[i] = -1
        plt.scatter(x_data[i], y_data[i], c='r')

w = 0
for i in range(n):
    w += alphas[i] * label_data[i] * data_matrix[i]
print(w)
# 画图，求x，y的最大最小值
x_min, x_max = x_data.min() - 1, x_data.max() + 1
y_min, y_max = y_data.min() - 1, y_data.max() + 1
# 网格化
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))
z = b + w[0] + w[1] * xx + w[2] * yy + w[3] * xx ** 2 + w[4] * xx * yy + w[5] * yy ** 2
# 利用等高线画出分类边界
plt.contour(xx, yy, z, [0])
plt.show()

可视化结果图：

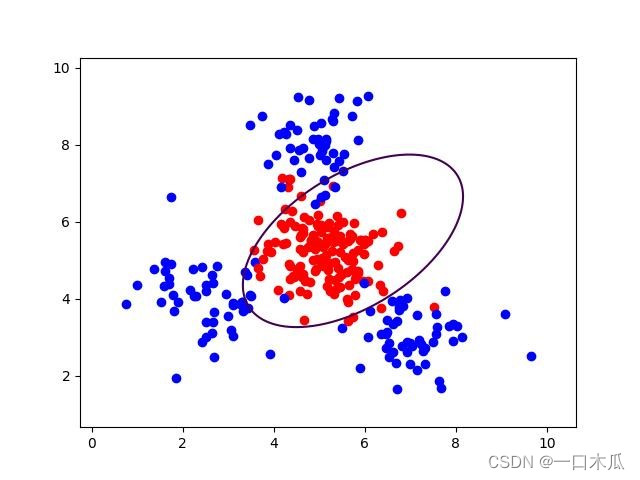
图2.2：二次多形式可视化结果图

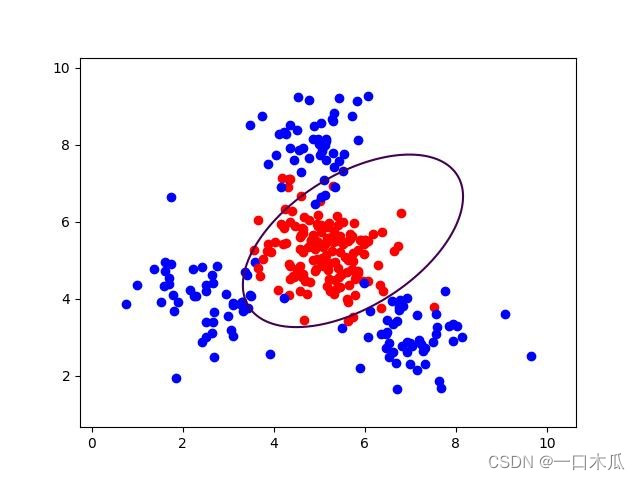
图2.3：三次多项式可视化结果图