时间序列分析（9）| 干扰分析-CSDN博客

本文链接：https://blog.csdn.net/weixin_54000907/article/details/125365030

本系列前面的推文仅涉及单变量时间序列的分析，从本篇起开始涉及多变量的分析。干扰分析（intervention analysis）研究的是外生变量对时间序列变量的影响作用。

1 干扰分析的形式

1.1 一般形式

干扰分析的一般模型形式如下：

402 Payment Required

其中，、为滞后算子的多项式，为外生变量，为系数。

需要为平稳序列；也就是说，在进行干扰分析前，应对原始序列数据进行单位根检验（包括可能发生结构化变化的情况），若原始序列为平稳序列，可以直接使用，若为非平稳序列，则需进行差分或去除趋势等平稳化操作。

1.2 滞后形式

如果干扰因素对时间序列数据的影响有延迟作用，可以取干扰变量的滞后形式：

402 Payment Required

1.3 干扰变量的形式

干扰因素的出现使得时间序列数据被分为两段：干扰前和干扰后。针对不同的情况，可以选取不同的变量形式来刻画干扰因素：

「虚拟变量」

若在时刻干扰因素存在，则，否则。

举例来说，若某项政策在时颁布后一直实行，则对于，可设；对于时，可设，这是一种「纯粹跳跃」的情况。

若某项特殊政策仅在时实行过一次，此后就恢复之前的状态了，那么可以仅在时设，其余时刻，这种情况也称为「脉冲」。

「渐进式」

这种形式是对纯粹跳跃的改进，即干扰因素不是一次性地从0跳跃到1，而是经历了一个渐进的过程。

比如，设，，，，此后均有。

「衰减式」

这种情况是对脉冲的改进。脉冲形式假定干扰因素是一下子消失的，而衰减式则假定干扰因素是逐渐衰减的，也就是说从1恢复为0需要经历一个过程。

比如，设，，，，此后均有。

2 模型估计过程

干扰模型的估计需要两个阶段：

「第一个阶段」：把时间序列分为干扰前和干扰后两段，选择其中较长的一段进行ARMA模型拟合，确定ARMA的阶数；

「第二个阶段」：以上个阶段确定的模型阶数为基础，使用完整序列数据（干扰前+干扰后）对干扰模型进行拟合，并对系数进行显著性检验。

3 案例

3.1 数据说明

本案例来自Walter Enders所著的Applied Econometric Time Series（第四版）第5章课后练习第2题。

示例数据可在公众号后台发送关键词「示例数据」获取（文件名为 131.Terrorism.XLS）。

关于该案例的详细说明请见原文。下面直接给出获取原始序列数据y的方法：

library(readxl)
data <- read_xls("131.Terrorism.XLS")
data$ENTRY <- paste(rep(1970:2010, each = 4), 1:4, sep = "-")
y = data$Transnational
plot(y, type = "l") 
abline(v = 112, lty = 2)

干扰发生在t = 113时，采取纯粹跳跃的形式定义干扰变量z：

z = rep(0, 164)
z[113:164] <- 1
z

##   [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
##  [38] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
##  [75] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## [112] 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [149] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

下面演示估计干扰模型的两个阶段（单位根检验过程略）。

3.2 第一阶段

时间序列的长度为164，其中干扰前为112，干扰后为52。干扰前的数据序列较长，因此使用它来确定阶数。

y1 = y[1:112]
acf(y1)
pacf(y1)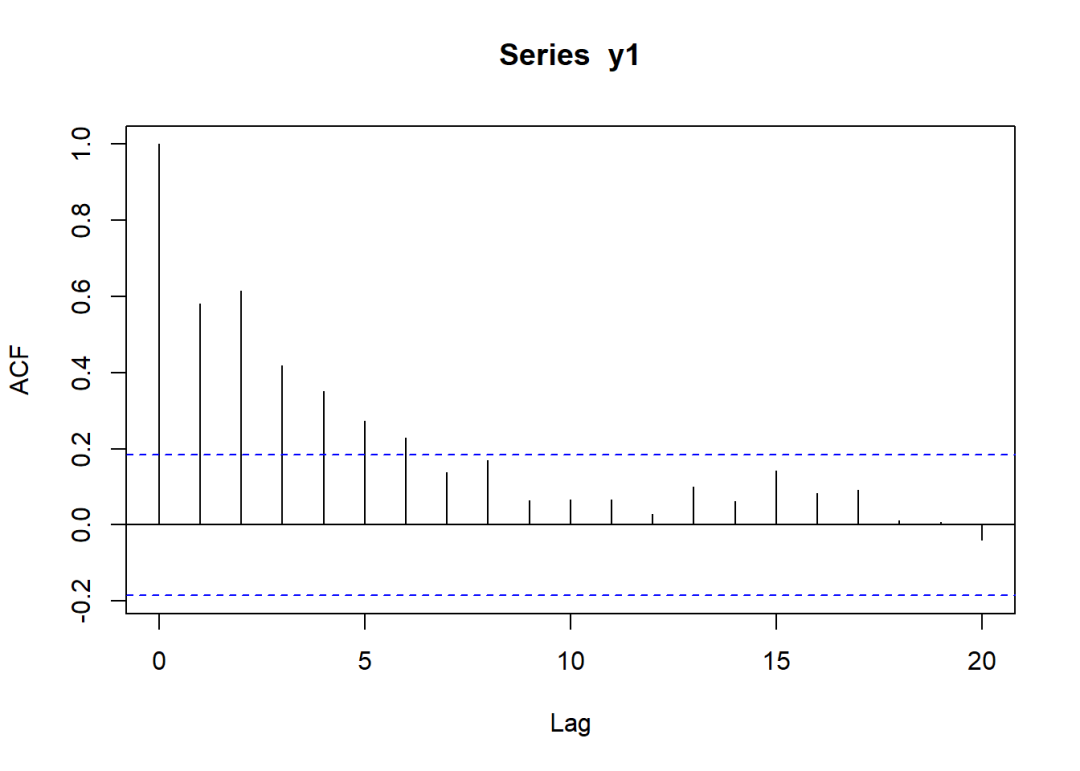

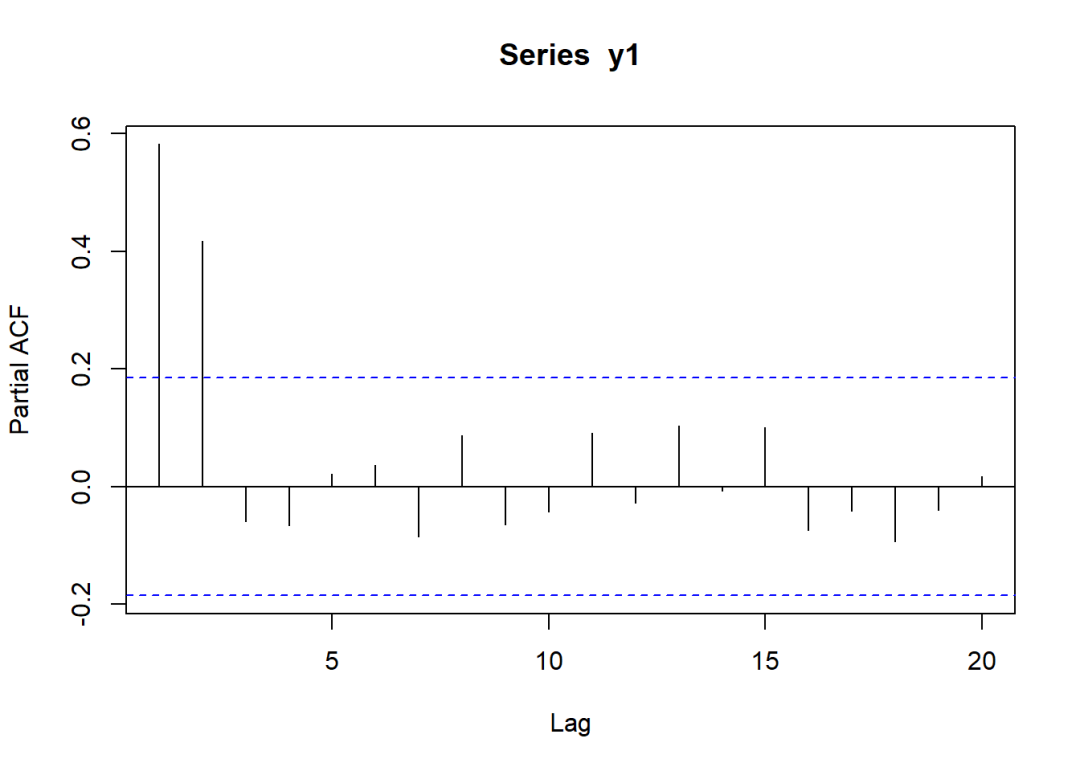
通过观察ACF和PACF图象可以有以下发现：

如果把PACF图象看作是截尾于，ACF图象呈衰减趋势，那么该过程很可能为AR(2)；
ACF图象在和时数值基本持平，而时相比之下明显下降，那么即使在保守估计的情况下，ACF也最迟在时开始衰减，因此。

根据以上发现，使用干扰前的序列y1拟合以下6个模型：

arima(y1, order = c(1,0,0))
## aic = 858.35

arima(y1, order = c(1,0,1)) 
## aic = 845.03

arima(y1, order = c(1,0,2)) 
## aic = 840.32

arima(y1, order = c(2,0,0)) 
## aic = 837.46

arima(y1, order = c(2,0,1)) 
## aic = 839.32

arima(y1, order = c(2,0,2)) 
## aic = 840.84

详细的模型信息请读者自行运行结果；
以AIC作为标准来看，AR(2)过程也是最优选择。

3.3 第二个阶段

使用完整时间序列y拟合AR(2)干扰模型。

arima()函数就可以完成在有外生解释变量的情况下对模型的估计，外生变量以矩阵或原子向量的形式赋值给参数xreg：

arima(y, order = c(2,0,0), xreg = z)

## Call:
## arima(x = y, order = c(2, 0, 0), xreg = z)
## 
## Coefficients:
##          ar1     ar2  intercept         z
##       0.3423  0.3903    28.6971  -14.8574
## s.e.  0.0718  0.0724     2.9517    4.6344
## 
## sigma^2 estimated as 79.27:  log likelihood = -591.63,  aic = 1193.27