spatialreg | 基于特征向量的空间滤波方法-CSDN博客

本文链接：https://blog.csdn.net/weixin_54000907/article/details/129173679

专注系列化、高质量的R语言教程

回归模型的残差不应当含有任何可以预测的成分。对于普通回归模型，我们通常需要检验残差的正态性（见推文：残差分析和异常点检验）；对于时间序列模型，我们通常需要检查残差是否为白噪音（见推文：ARMA模型的拟合）；而对于空间计量模型来说，我们也应检查残差是否具有空间自相关性。

本篇目录如下：

1 引例
2 理论基础
3 SpatialFiltering函数
4 与空间误差模型的比较

1 引例

加载示例数据：

library(sf)
columbus <- st_read(system.file("shapes/columbus.shp",
                                package="spData")[1], quiet = TRUE)
plot(st_geometry(columbus))

先把columbus当作普通的数据框，使用它的变量建立一个普通的线性模型：

lmbase <- lm(CRIME ~ INC + HOVAL, data = columbus)
summary(lmbase)
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  68.6190     4.7355  14.490  < 2e-16 ***
## INC          -1.5973     0.3341  -4.780 1.83e-05 ***
## HOVAL        -0.2739     0.1032  -2.654   0.0109 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 11.43 on 46 degrees of freedom
## Multiple R-squared:  0.5524, Adjusted R-squared:  0.5329 
## F-statistic: 28.39 on 2 and 46 DF,  p-value: 9.341e-09

变量系数都具有较好的显著性。

下面使用plot()函数绘制残差分析图：

par(mfrow = c(2,2))
plot(lmbase)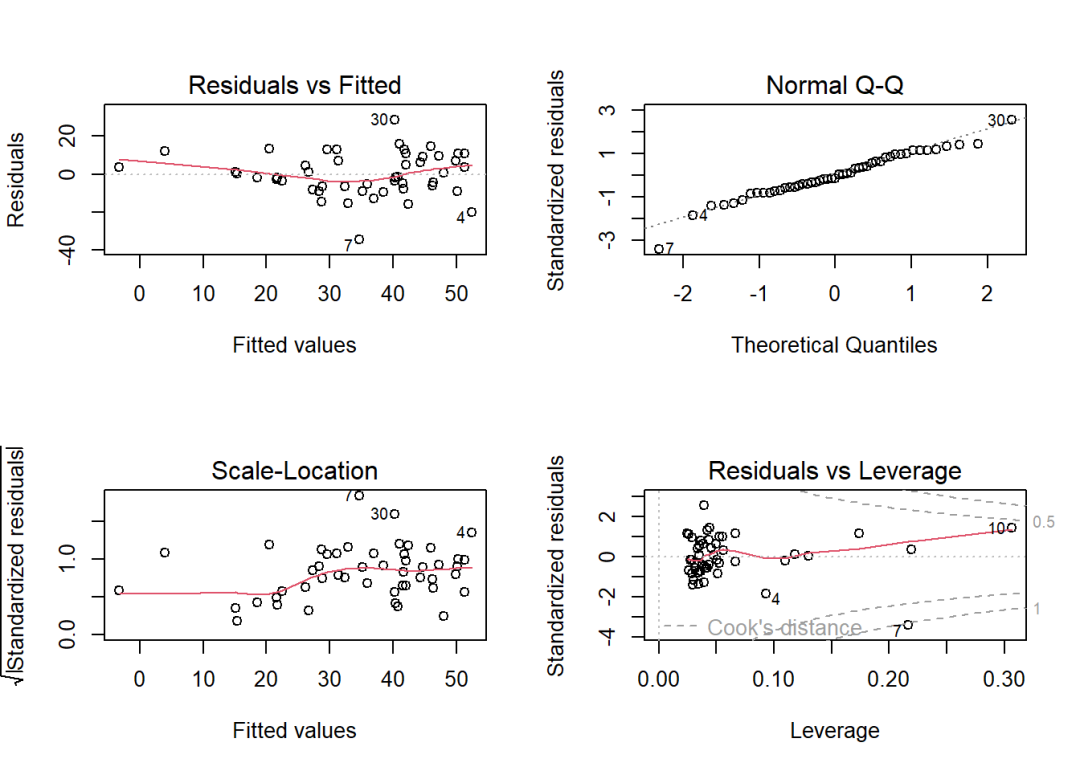

从右上角的图片可以看出，模型的残差基本上符合正态分布。因此从评价普通模型的角度看，该模型已经比较优秀了。

下面使用莫兰指数（见推文：如何在R语言中计算空间自相关指数）检验残差的空间相关性：

library(spdep)
nb <- poly2nb(columbus) 
w = nb2listw(col.gal.nb)

columbus$res_base <- residuals(lmbase)
plot(columbus["res_base"])

moran.test(columbus$res_base, w)
## Moran I statistic standard deviate = 2.5027, p-value = 0.006162
## alternative hypothesis: greater
## sample estimates:
## Moran I statistic       Expectation          Variance 
##       0.212374153      -0.020833333       0.008682862

结果显示，模型残差具有显著的正向自相关（Moran'I = 0.21，p = 0.006162）。

2 理论基础

在上面的例子中，模型残差在空间上呈现显著的自相关，因此残差独立性假设遭到否定。空间滤波（Spatial Filtering）方法是解决这一问题的方法之一。

首先考虑类似线性回归的模型形式：

上式中，残差使用表示而不是，是因为它并不一定是随机分布的，在空间上可能具有自相关性。

空间滤波方法的思想是将上述残差的可预测部分分离出来，表示为如下式子：

其中，是行矩阵，每列表示一个变量，为其系数；是残差的不可预测部分，在空间上不具有显著的自相关。

下面是基于特征向量的空间滤波（Eigenvector-Based Spatial Filtering，ESF）方法的步骤^[1]。

使用表示自变量组成的矩阵（第一列元素均为1，对应截距；其余列为自变量），则矩阵：

其中，为单位矩阵，表示转置矩阵，表示矩阵的逆。

使用表示空间权重矩阵，令，则矩阵的特征向量就可以作为预测模型残差的变量。

记特征向量组成的矩阵为，它的的大小为（为样本数），对应个变量。显然，我们不可能向模型中加入个变量（会导致预测变量大于样本数），而应从中挑选若干列（特征向量）作为滤波向量组成。挑选特征向量的方法参见文献[1]。

3 SpatialFiltering函数

SpatialFiltering()函数来自spatialreg工具包，它可以应用于线性模型的空间滤波。

提取引例中所示线性模型的滤波变量：

library(spatialreg)
sarcol <- SpatialFiltering(formula = CRIME ~ INC + HOVAL, 
                           data = columbus,
                           nb = nb, style = "W", 
                           ExactEV = TRUE) 
sarcol
##   Step SelEvec      Eval       MinMi      ZMinMi      Pr(ZI)        R2     gamma
## 0    0       0 0.0000000  0.22210941  2.83931893 0.004520994 0.5524040   0.00000
## 1    1       5 0.7055627  0.12569332  1.97146869 0.048670291 0.6268268  31.62450
## 2    2       3 0.8402366  0.05839274  1.48499817 0.137544308 0.6589493  20.77665
## 3    3       1 1.0042462 -0.02137880  0.90639639 0.364726085 0.6854757 -18.88035
## 4    4      10 0.3408136 -0.07305118  0.39536350 0.692574639 0.7247450 -22.97196
## 5    5      14 0.1880578 -0.11636686 -0.04537581 0.963807762 0.7639102  22.94146

formula和data参数同原模型lmbase；
nb为空间邻接矩阵；style表示空间权重矩阵类型（含义见推文：如何在R语言中计算空间自相关指数第2.1部分）；
输出结果展示了特征向量的挑选过程，最终第5、3、1、10、14个特征向量依次被选中。

输出由选中的特征向量组成的矩阵：

fitted(sarcol)
##              vec5         vec3         vec1         vec10        vec14
##  [1,]  0.17887760 -0.205796962  0.010875150  0.0482621810  0.014453709
##  [2,]  0.14822809 -0.177830005  0.006197033  0.0581042914 -0.039955565
##  [3,]  0.09777111 -0.138272425  0.004335059  0.0297948218 -0.037013854
##  [4,] -0.02881867 -0.080677214  0.017066900  0.0809334369 -0.034397747
##  [5,] -0.16092377  0.096932614 -0.006864207 -0.2149403333  0.092553448
##  [6,] -0.11795983  0.089288848 -0.028430064 -0.3279265353 -0.128678299
##  ...

然后，在原模型的基础上加入fitted(sarcol)作为自变量：

lmsar <- lm(CRIME ~ INC + HOVAL + fitted(sarcol), data = columbus)
summary(lmsar)
## Coefficients:
##                      Estimate Std. Error t value Pr(>|t|)    
## (Intercept)          68.61896    3.64290  18.836  < 2e-16 ***
## INC                  -1.59731    0.25704  -6.214 2.14e-07 ***
## HOVAL                -0.27393    0.07939  -3.451 0.001310 ** 
## fitted(sarcol)vec5   31.62450    8.79665   3.595 0.000863 ***
## fitted(sarcol)vec3   20.77665    8.79665   2.362 0.023013 *  
## fitted(sarcol)vec1  -18.88035    8.79665  -2.146 0.037816 *  
## fitted(sarcol)vec10 -22.97196    8.79665  -2.611 0.012539 *  
## fitted(sarcol)vec14  22.94146    8.79665   2.608 0.012648 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8.797 on 41 degrees of freedom
## Multiple R-squared:  0.7639, Adjusted R-squared:  0.7236 
## F-statistic: 18.95 on 7 and 41 DF,  p-value: 5.219e-11

相比于原模型，lmsar的截距和变量系数基本保持不变（(Intercept)、INC、HOVAL），但显著性增强；
新加入的特征向量的系数都是显著的（特征向量挑选的意义）。

最后再来检验模型残差的空间自相关性：

columbus$res_sar <- residuals(lmsar)
plot(columbus["res_sar"])  

moran.test(columbus$res_sar, w)
## Moran I statistic standard deviate = -1.1929, p-value = 0.8835
## alternative hypothesis: greater
## sample estimates:
## Moran I statistic       Expectation          Variance 
##      -0.131421926      -0.020833333       0.008594783

结果显示，不能认为残差具有空间自相关性（p = 0.8835）。

4 与空间误差模型的比较

学堂君在推文空间滞后模型、空间误差模型和空间杜宾模型简单形式的R语言实现中介绍过空间误差模型。

使用同一示例数据运行空间残差模型：

lmsem <- errorsarlm(CRIME ~ INC + HOVAL,
                    data = columbus, listw = w,
                    zero.policy = T)
summary(lmsem)
## Type: error 
## Coefficients: (asymptotic standard errors) 
##              Estimate Std. Error z value  Pr(>|z|)
## (Intercept) 61.053618   5.314875 11.4873 < 2.2e-16
## INC         -0.995473   0.337025 -2.9537 0.0031398
## HOVAL       -0.307979   0.092584 -3.3265 0.0008794
## 
## Lambda: 0.52089, LR test value: 6.4441, p-value: 0.011132
## Asymptotic standard error: 0.14129
##     z-value: 3.6868, p-value: 0.00022713
## Wald statistic: 13.592, p-value: 0.00022713
## 
## Log likelihood: -184.1552 for error model
## ML residual variance (sigma squared): 99.98, (sigma: 9.999)
## Number of observations: 49 
## Number of parameters estimated: 5 
## AIC: 378.31, (AIC for lm: 382.75)

检验模型残差：

## 残差检验
columbus$res_sem <- residuals(lmsem)
plot(columbus["res_sem"])  

moran.test(columbus$res_sem, w)
## Moran I statistic standard deviate = 0.32245, p-value = 0.3736
## alternative hypothesis: greater
## sample estimates:
## Moran I statistic       Expectation          Variance 
##       0.008970641      -0.020833333       0.008543294

空间误差模型的变量系数不同于原模型（lmbase）；
空间误差模型的残差也不具有显著的空间自相关性（p = 0.3736）。

本篇主要介绍了针对线性模型的空间滤波方法，后面还会介绍针对广义线性模型的空间滤波方法。

参考资料

[1]

spfilteR: An R package for Semiparametric Spatial Filtering with Eigenvectors in (Generalized) Linear Models: https://journal.r-project.org/archive/2021/RJ-2021-085/RJ-2021-085.pdf