MATLAB学习（5）--线性方程组的数值解

最新推荐文章于 2024-03-23 11:42:15 发布

cccccccc6666666666

最新推荐文章于 2024-03-23 11:42:15 发布

阅读量3k

点赞数 3

文章标签： matlab 学习

本文链接：https://blog.csdn.net/weixin_54379099/article/details/126632756

版权

关于线性方程组的数值解法一般分为两类：

一类是直接法，就是在没有舍入误差的情况下，通过有限步四则运算求得方程组准确解的方法。直接法主要包括矩阵相除法和消去法；

另一类是迭代法，就是先给定一个解的初始值，然后按一定的法则逐步求出解的近似值的方法。

直接法

1. 矩阵相除法

在 MATLAB 中，线性方程组 AX = B 的直接解法是用矩阵除来完成的，即 X = A\B 。若

A 为 m × n 的矩阵，当 m = n 且 A 可逆时，给出唯一解；当 n > m 时，矩阵除给出方程的

最小二乘解；当 n < m 时，矩阵除给出方程的最小范数解

由此得知方程组的解为 $x_{1}=4,x_{2}=3,x_{3}=-2$

注意：矩阵 B 为列向量。

2. 消去法

方程的个数和未知数个数不相等，用消去法。将增广矩阵 ( 由 [A B] 构成 ) 化为简化阶梯

形，若系数矩阵的秩不等于增广矩阵的秩，则方程组无解；若两者的秩相等，则方程组有

解，方程组的解就是行简化阶梯形所对应的方程组的解。

迭代法

迭代法是指用某种极限过程去逐步逼近线性方程组的精确解的过程，迭代法是解大型

稀疏矩阵方程组的重要方法。相比较于 Gauss 消去法、列主元消去法、平方根法这些直接

法来说，迭代法具有求解速度快的特点，在计算机上计算尤为方便。

在线性方程组中常用的迭代解法主要有 Jacobi 迭代法、 Gauss-Seidel 迭代法、 SOR( 超

松弛 ) 迭代法等。下面分别进行讨论。

1 ． Jacobi 迭代法

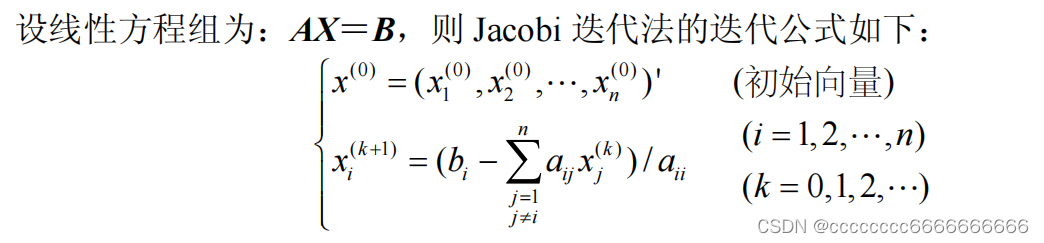
function tx=jacobi(A,b,imax,x0,tol) %利用 jacobi 迭代法解线性方程组 AX=b，迭
 %代初值为 x0，迭代次数由 imax 提供，精确
%度由 tol 提供
del=10^-10; %主对角的元素不能太小，必须大于 del 
tx=[x0] ; n=length(x0); 
for i=1:n 
 dg=A(i,i); 
 if abs(dg)< del 
 disp('diagonal element is too small'); 
 return 
 end 
 end 
for k = 1:imax %Jacobi 迭代法的运算循环体开始
 for i = 1:n 
 sm=b(i) ; 
 for j = 1:n 
 if j~=i 
 sm = sm -A(i,j)*x0(j) ; 
 end 
 end %for j 
 x(i)=sm/A(i,i) ; %本次迭代得到的近似解
 end 
 tx=[tx ;x] ; %将本次迭代得到的近似解存入变量 tx 中
 if norm(x-x0)<tol 
 return 
 else 
 x0=x ; 
 end 
end %Jacobi 迭代法的运算循环体结束

上面书上给的代码在套用时出了问题，换了一个代码;

function x=jacobi_fun(A,b,n,x0,tol,N)
x=zeros(n,1);      % 给x赋值
k=0;
while k<N
    for i=1:n
     x(i)=(b(i)-A(i,[1:i-1,i+1:n])*x0([1:i-1,i+1:n]))/A(i,i);
    end
    if norm(x-x0)<tol
        break;
    end
    x0=x;
    k=k+1;

    disp(['when k=',num2str(k)])
    disp('x=');
    disp(x);                       %输出计算的中间结果
end

if k==N
    disp('迭代次数已到达上限!');
end
disp(['迭代次数 k=',num2str(k)])

end

http://t.csdn.cn/NKi0D

>> A=[10 -1 -2;-1 10 -2;-1 -1 5];
b=[72;83;42];
n=3;
x0=[0;0;0];
tol=1e-6;
N=500;
>> x=jacobi_fun(A,b,n,x0,tol,N)
when k=1
x=
    7.2000
    8.3000
    8.4000

when k=2
x=
    9.7100
   10.7000
   11.5000

when k=3
x=
   10.5700
   11.5710
   12.4820

when k=4
x=
   10.8535
   11.8534
   12.8282

when k=5
x=
   10.9510
   11.9510
   12.9414

when k=6
x=
   10.9834
   11.9834
   12.9804

when k=7
x=
   10.9944
   11.9944
   12.9933

when k=8
x=
   10.9981
   11.9981
   12.9978

when k=9
x=
   10.9994
   11.9994
   12.9992

when k=10
x=
   10.9998
   11.9998
   12.9997

when k=11
x=
   10.9999
   11.9999
   12.9999

when k=12
x=
   11.0000
   12.0000
   13.0000

when k=13
x=
   11.0000
   12.0000
   13.0000

when k=14
x=
   11.0000
   12.0000
   13.0000

when k=15
x=
   11.0000
   12.0000
   13.0000

when k=16
x=
   11.0000
   12.0000
   13.0000

迭代次数 k=16

x =

   11.0000
   12.0000
   13.0000

可以看到迭代次数越高，精度越高

2 ． Gauss-Seidel 迭代法

function tx= gseidel( A,b,imax,x0,tol)%利用 Gauss-Seidel 迭代法解线性方程组
%AX=b，迭代初值为 x0，迭代次数由 imax 提 %供，精确度由 tol 提供
del=10^-10; %主对角的元素不能太小，必须大于 del 
tx=[x0]; n=length(x0); 
for i=1:n 
 dg=A(i,i); 
 if abs(dg)< del 
 disp('diagonal element is too small'); 
 return 
 end 
end 
for k = 1:imax %Gauss-Seidel 迭代法的运算循环体开始
 x=x0; 
 for i = 1:n 
 sm=b(i); 
 for j = 1:n 
 if j~=i 
 sm = sm -A(i,j)*x(j); 
 end 
 end 
 x(i)=sm/A(i,i); 
 end 
 tx=[tx;x]; %将本次迭代得到的近似解存入变量 tx 中
 if norm(x-x0)<tol 
 return 
 else 
 x0=x; 
 end 
end % Gauss-Seidel 迭代法的运算循环体结束

A=[10 -1 2 0;-1 11 -1 3;2 -1 10 -1;0 3 -1 8]; 
b= [6 25 -11 15]'; 
tol=1.0*10^-6 ; 
imax =10; 
x0= zeros(1,4); 
tx =gseidel(A,b,imax,x0,tol); 
for j=1:size(tx,1) 
 fprintf('%4d %f %f %f %f\n', j, tx(j,1),tx(j,2),tx(j,3),tx(j,4)) 
 end
   1 0.000000 0.000000 0.000000 0.000000
   2 0.600000 2.327273 -0.987273 0.878864
   3 1.030182 2.036938 -1.014456 0.984341
   4 1.006585 2.003555 -1.002527 0.998351
   5 1.000861 2.000298 -1.000307 0.999850
   6 1.000091 2.000021 -1.000031 0.999988
   7 1.000008 2.000001 -1.000003 0.999999
   8 1.000001 2.000000 -1.000000 1.000000
   9 1.000000 2.000000 -1.000000 1.000000

3 ． SOR( 超松弛 ) 迭代法

超松弛迭代法是目前解大型线性方程组的一种最常用的方法，是 Gauss-Seidel 迭代法

的一种加速方法。迭代公式为

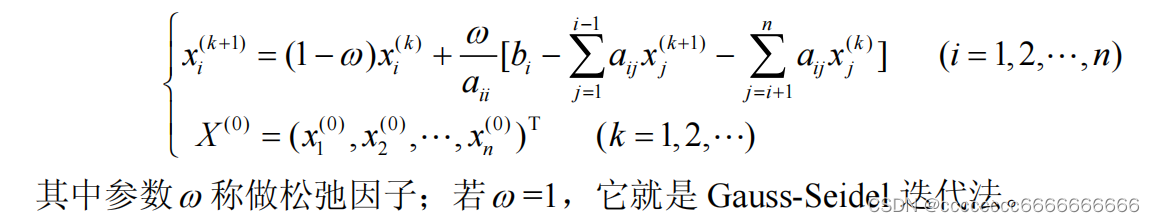
function tx = sor( A,b,imax,x0,tol,w) %利用 Gauss-Seidel 迭代法解线性方程组
%AX=b，迭代初值为 x0，迭代次数由 imax 
%提供，精确度由 tol 提供，w 为松弛因子
del=10^-10; %主对角的元素不能太小，必须大于 del 
tx=[x0] ; n=length(x0); 
for i=1:n 
 dg=A(i,i); 
 if abs(dg)< del 
 disp('diagonal element is too small'); 
 return 
 end 
end 
for k = 1:imax %SOR 迭代法的运算循环体开始
 x=x0 ; 
 for i = 1:n
     sm=b(i); 
 for j = 1:n 
 if j~=i 
 sm = sm -A(i,j)*x(j); 
 end 
 end 
 x(i)=sm/A(i,i); %本次迭代得到的近似解
 x(i)=w*x(i)+(1-w)*x0(i); 
 end 
 tx=[tx;x]; %将本次迭代得到的近似解存入变量 tx 中
 if norm(x-x0)<tol 
 return 
 else 
 x0=x; 
 end 
end %SOR 迭代法的运算循环体结束